99클럽 코테 스터디 11일차 TIL + 깊이/너비 우선 탐색(DFS/BFS) 타겟 넘버

문제

링크텍스트

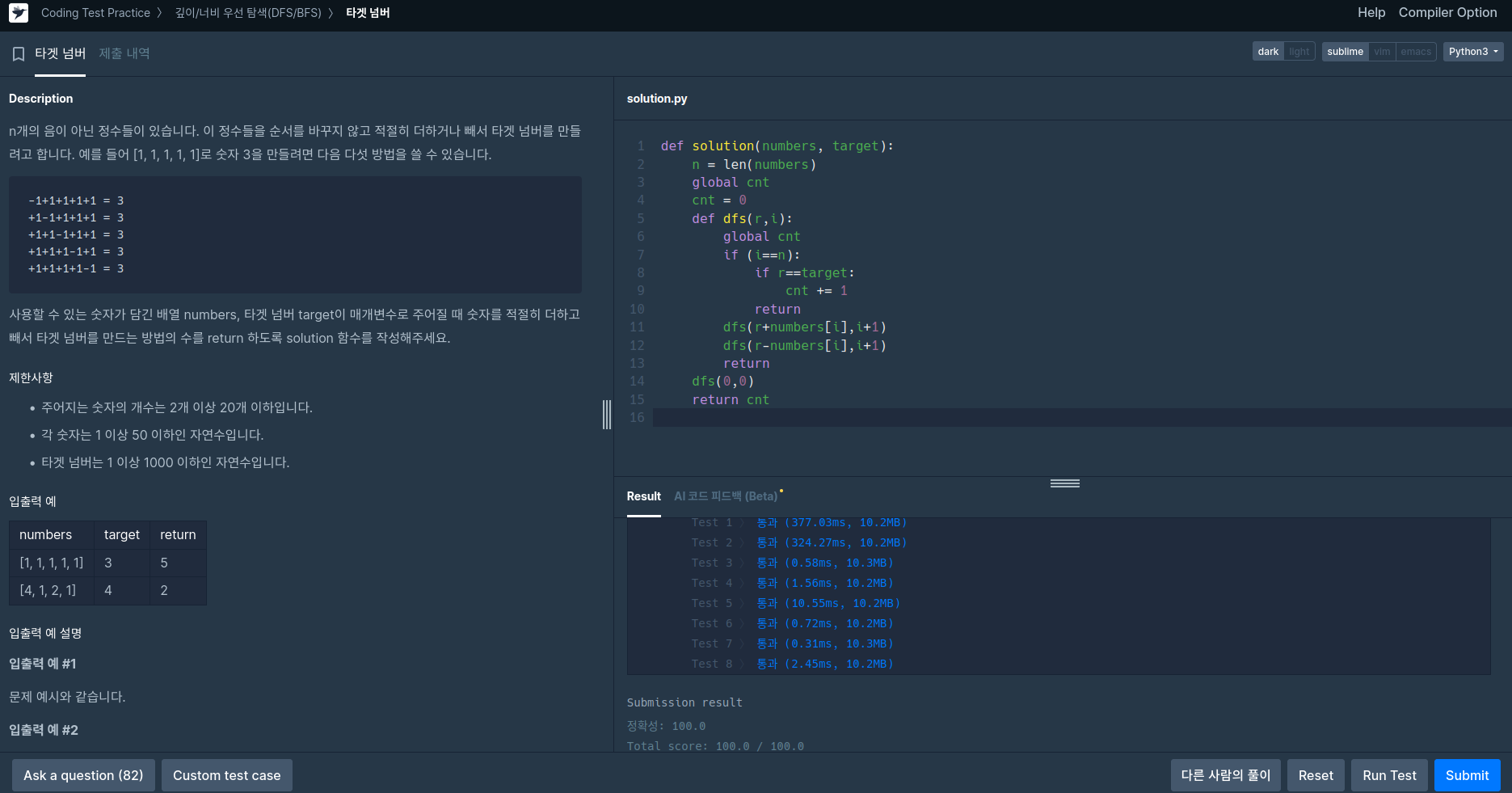
recursive를 사용한 풀이

• 주어진 각각의 정수들에 +/- 연산자를 적용해 나가며, 최종 연산 결과를 확인합니다.
• 여기서 재귀함수의 종료 조건은 모든 정수에 연산자를 다 적용했는지이며,
  • 특히, 최종 연산 결과가 target과 같으면 cnt를 하나 증가시킵니다.
• 종료 조건을 만족시키지 못하면, 즉, 아직 연산자를 적용할 정수가 남아있다면,
  • 재귀함수를 다시 부릅니다.
• 재귀하는 개별 함수가 가져야 할 state는 다음과 같습니다.
  • 개별 함수의 재귀 단계
  • 재귀 단계까지 그동안의 연산 결과
  • cnt: 타겟 넘버를 만드는 방법의 수
• cnt를 없앤 다음의 풀이를 다른 99클럽 멤버의 블로그에서 찾았습니다. 하양이노랑이

def solution(numbers, target):
    def dfs(idx,total):
        if idx==len(numbers):
            return 1 if target==total else 0
        return dfs(idx+1,total+numbers[idx]) + dfs(idx+1,total-numbers[idx])
    return dfs(0,0)

결과

def solution(numbers, target):
    n = len(numbers)
    def dfs(r,i,cnt):
        if i==n:
            if r==target:
                cnt += 1
                return cnt
            return cnt
        cnt = dfs(r+numbers[i],i+1,cnt)
        cnt = dfs(r-numbers[i],i+1,cnt)
        return cnt
    cnt = dfs(0,0,0)
    return cnt

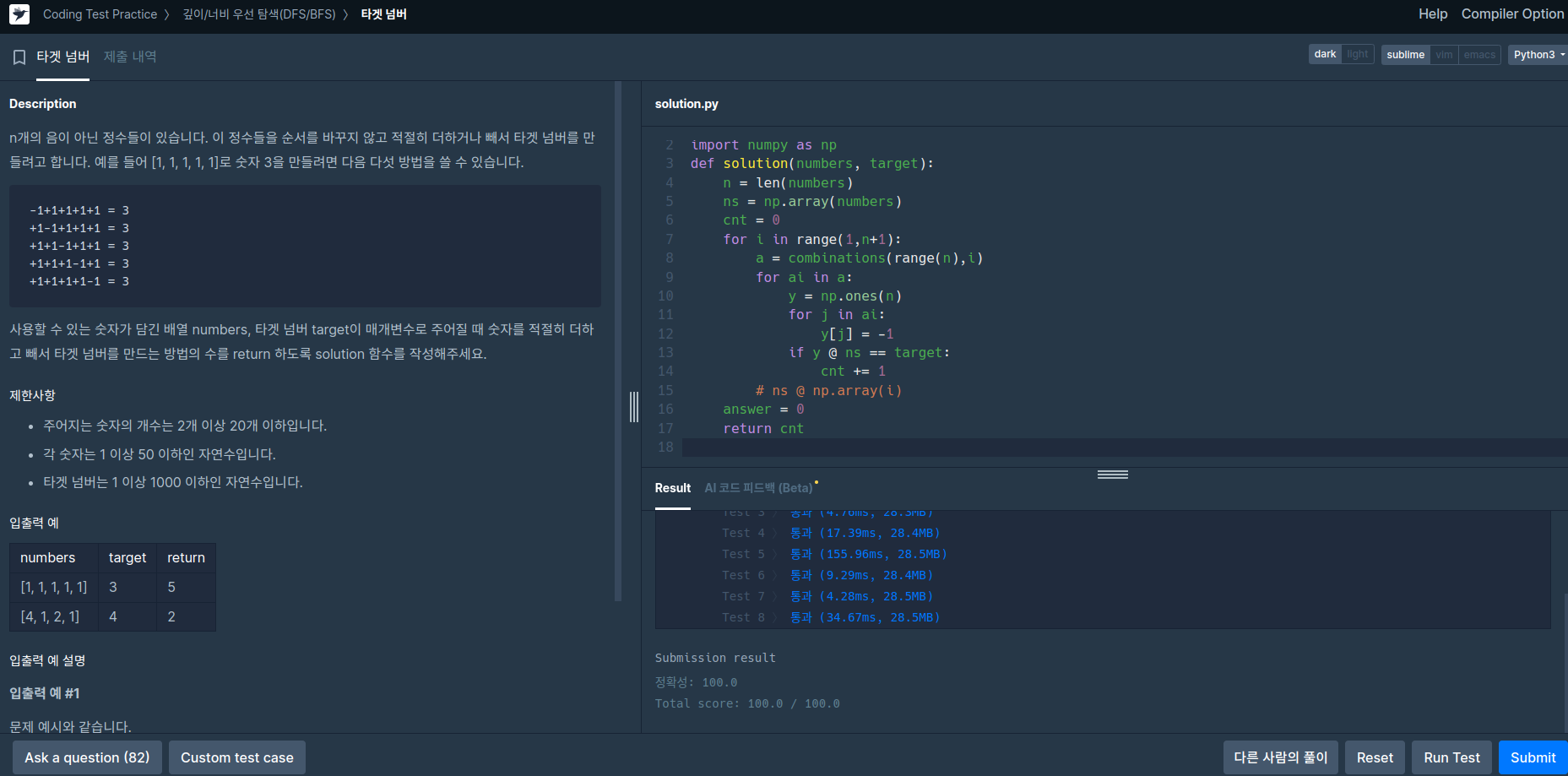
풀이

• DFS를 사용하지 못했습니다.
• 모각코 시간에 다시 풀려고 합니다.
• combination을 사용하여 +/- 연산자의 가능한 모든 조합을 구합니다.
• 그리고 각 조합에 대하여 최종 연산을 확인하여 target을 만족하는 경우를 합산합니다.
• 최종 연산 확인 시간을 줄이기 위하여, numpy의 벡터 내적을 사용했습니다.

결과

def f_t(id_t):
    if id_t == 0:
        numbers, target, r = [1, 1, 1, 1, 1],	3,	5
    if id_t == 1:
        numbers, target, r = [4, 1, 2, 1],	4,	2        
    return numbers, target, r

from itertools import combinations
import numpy as np
def solution(numbers, target):
    n = len(numbers)
    ns = np.array(numbers)
    cnt = 0
    for i in range(1,n+1):
        a = combinations(range(n),i)
        for ai in a:
            y = np.ones(n)
            for j in ai:
                y[j] = -1
            if y @ ns == target:
                cnt += 1
    return cnt
    
for i in range(2):
    print(f'test case {i}')
    numbers, target, r = f_t(i)
    a = solution(numbers, target)
    print(a)
    print(r)