교육

제로베이스_데이터분석취업스쿨

강의

선형대수 챕터01~03
(벡터, 행렬, 선형대수학)

느낀점

파이썬과 sql을 공부하면서, 데이터가 표 형식으로 이루어진 것을 볼 수 있었다. 표는 행렬의 모습을 하고 있기 때문에 벡터~선형대수학을 배운 이유는 앞으로 데이터분석을 하는데 있어 각 값을 구할 때 행렬로서 구하기 위함이라고 생각했다. 따라서 주어진 개념과 예시 문제를 볼 때 각 데이터를 단순히 숫자로서 생각하지 않고, 최대한 어떤 주제에 대한 데이터값이라고 상상하며 강의를 들었다. 또한 타 부트캠프와 달리 데이터분석에서 선형대수학을 가르치는 것은 무척 중요하다는 글들을 많이 보았기 때문에, 특히 집중했다. 학부시절 경제학과 수업을 처음 들을 때 다양한 공식과 개념들에 단련되었기 때문에, 배운 내용을 충분히 반복 복습하고자 한다. 또한 앞으로 강의를 들으며 선형대수가 이래서 적용되었구나라는 것을 하루빨리 몸소 경험해보고 싶다.

수업 내용

챕터01. 벡터(Vector)

- 벡터의 정의와 표기법

• 벡터란?

  벡터라는 단어는 라틴어에서 비롯함

  벡터의 역사를 사려보았을 때 이 단어가 나타난지는 그리 오래 되지 않았음

  옥스퍼드 사전에는 1704년에 출간된 존 헤리스의 저서에 벡터라는 단어가 처음 등장

  라틴어 Vector는 운반하는 물체를 뜻하며 영어로는 캐리어(Carrier)로 번역 가능

  우리 주변의 세계를 보고 이를 코드로 영리하게 묘사하는 방법

  사과가 나무에서 떨어지고, 추가 공중에서 흔들리고, 지구가 태양을 중심으로 움직이는 현상 표현 모두 ‘벡터’ 개념이 들어가 있음

  벡터는 사물의 움직임을 프로그래밍하기 위한 가장 기본적인 구성요소

  벡터는 크기와 방향을 모두 가지는 어떤 양으로 정의 됨

  물리학 및 공학에서 벡터는 위치, 속도, 힘 등과 같이 크기와 방향성을 나타냄

  공학에서는 벡터 공간이 유클리드 공간인 경우를 대부분 다룸

  따라서 유클리드 벡터(Euclidean Vector), 기하 벡터(Geometric Vector), 공간 벡터(Spatial Vector)라고 부름

  벡터와 대비하여 크기만을(길이, 높이, 질량, 에너지) 갖는 대상을 스칼라(Scalar)라고 함

• 벡터의 표기법

  한 벡터를 부호 a를 사용하여 나타낼 때, a, a(물결), a(방향) 등과 같이 표기함
  a의 크기만을 나타낼 때는 lal, a 등의 방법으로 표기
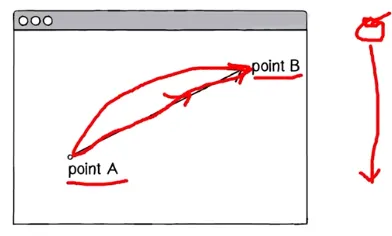
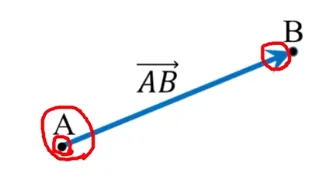
  점 A에서 점 B를 향하며, 크기가 두 점 사이를 잇는 선분의 길이인 벡터와 부호를 사용하여 나타낼 때, 대게 AB(위 →)와 같이 표현함
  A를 화살표의 원점, 기점, 꼬리라고 하며 B는 화살표의 끝, 종점, 머리라고 표현

- 벡터의 기본적인 성질

• 벡터의 기본적인 성질

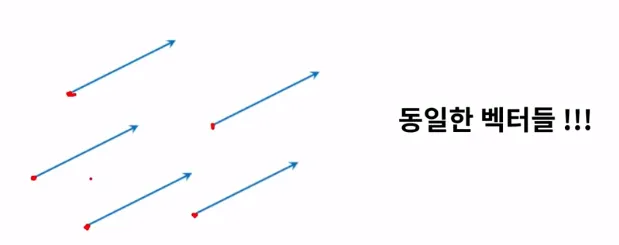
  동등성 : 벡터가 크기와 방향만을 가지므로 원점의 특정한 위치는 아무런 의미를 갖지 않음. 즉 원점이 일치하지 않더라도 두 화살표의 방향이 일치하고 그 크기가 같으면, 동일한 벡터임

  영벡터 : 영벡터는 크기가 0인 벡터를 의미함

  음벡터 : 벡터 a 자신에 더했을 때 결과가 영벡터가 되는 벡터를 a의 음벡터라고 정의함. -a로 표시하고 음벡터 -a는 a와 크기는 같으나 방향이 정반대인 벡터를 의미함

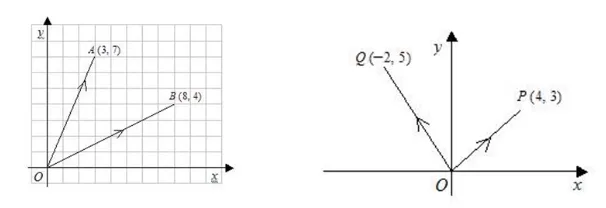
• 벡터의 좌표와 성분

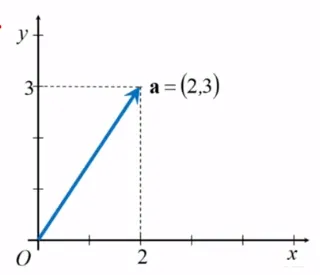
  벡터를 표현하는 방법으로는 공간에 좌표계를 설정하여 좌표 값을 사용할 수 있음

  기하학적으로는 벡터를 다루는 방법보다 편리하며, 보다 체계적으로 정확한 계산을 할 수 있음

  가장 흔한 예로는 직각좌표계를 사용함. 한 벡터의 기점을 좌표계의 원점으로 하고 벡터의 종점의 좌표로 해당 벡터를 표시함

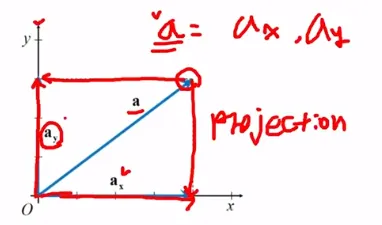
• 벡터의 성분, 분해, 합성

  벡터의 성분은 각각의 좌표축에 벡터를 투영시켜(Projection) 얻음.

  이 또한 벡터이므로 성분벡터(Component vector, a_x, a_y)라고 부름

  따라서 a_x, a_y는 “벡터 a의 축 성분벡터”라고 부름

  이것은 2차원 이상의 공간에서는 차원의 수만큼 성분이 존재하며, 차원을 확장하여 적용 가능

  a = a_x + a_y로 표현이 가능함

  한 벡터를 자신의 성분벡터들의 합으로 나타내는 것을 벡터의 분해라고 함.

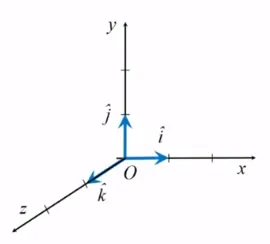
• 단위벡터

  벡터의 성분 표시를 편리하게 하기 위해 추가적인 단위벡터를 도입할 수 있음

  단위벡터는 크기가 1이며, 특정한 방향을 갖는 벡터임. 벡터의 방향을 나타내기 위할 뿐 차원과 단위가 없음.

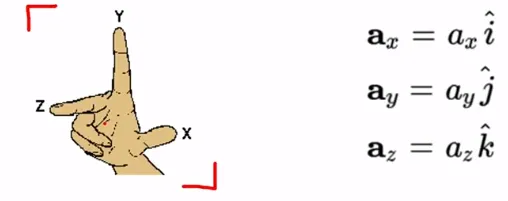
  3차원의 직각좌표계 (X, Y, Z)가 주어질 때, 각 좌표축에 나란한 방향을 갖는 단위벡터를 각각 i(위 ^), j(위 ^), k(위 ^)라고 나타냄. (i햇, j햇, k햇)

  축의 방향은 ‘오른나사 규칙’, ‘오른손 규칙’의 관례를 따라 정한 것

  모든 좌표축에 대한 단위 벡터들의 집합 {i햇, j햇, k햇}을 기저벡터 집합 (basis vectors)라고 부름

  특정 기저벡터 집합을 선택하는 것은 특정한 직각좌표계를 선택하는 것과 동등

  스칼라 배(Scalar multiplication)의 정의를 이용하여 벡터 a의 성분 벡터들은 각각 아래와 같이 표현할 수 있음

  여기서 벡터들과 함께 벡터 공간에 연관된 스칼라인 a_x, a_y, a_z를 벡터의 성분이라고 부름

  a = a_x i햇 + a_y j햇 + a_z k햇 또는 a = (a_x, a_y, a_z)

- 벡터의 연산1

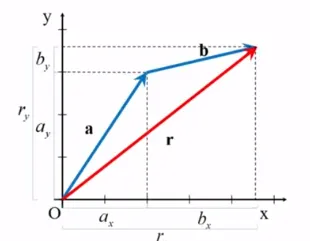
• 벡터의 덧셈

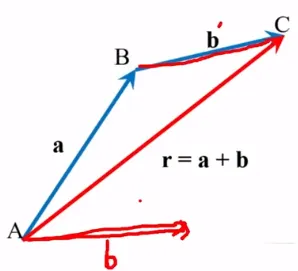
  기하학적인 방법 1 삼각형법 (Tail - to - tip method)

  공간 상의 위치는 벡터량임. 위치의 변화인 변위(displacement)도 벡터량임

  r = a + b

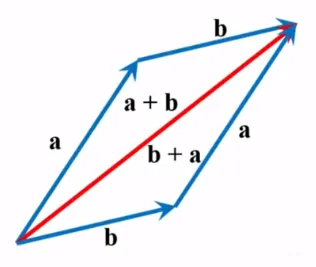
• 덧셈의 교환법칙

  그림에서 명백하게 보여주듯, 두 벡터의 순서가 바뀌어도 결관는 마찬가지임

  이를 ‘벡터의 덧셈이 교환법칙을 만족시킨다’라고 말함

  a + b = b + a

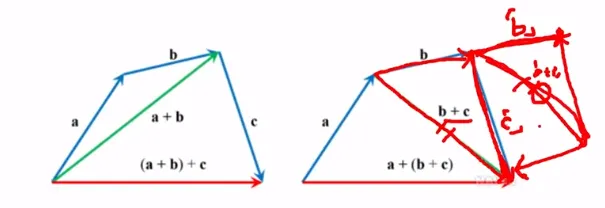
• 덧셈의 결합법칙

  그림에서 명백하게 보여주듯, 더하는 벡터들이 두 개 이상인 경우에도, 더하는 순서에 상관없이 결과는 동일함

  이를 ‘벡터의 덧셈이 결합법칙을 만족시킨다’라고 말함

  (a + b) + c = a + (b + c)

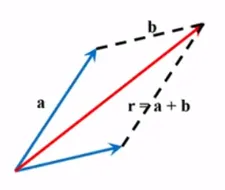
• 기하학적인 방법 2 - 평행사변형법 (Parallelogram method)

  B를 평행이동하여, a와 b의 꼬리를 일치시킨 후, 두 벡터를 인접한 두 변으로 하는 평행사변형을 그렸을 때, 두 벡터의 꼬리에서 시작하는 평행사변형의 대각선이 a와 b의 합벡터에 해당됨

  이것이 삼각형법과 같은 결과를 준다는 사실은 그림으로 입증

• 성분을 이용한 대수적인 방법

  두 벡터가 동일하다면 대응하는 벡터의 성분이 반드시 같아야 함

  r_x = a_x + b_x, r_y = a_y + b_y

  r = r_x + r_y

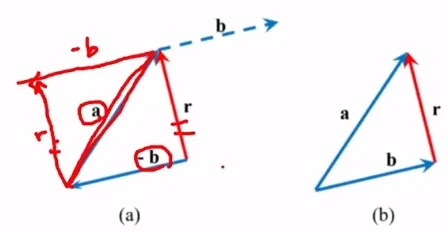
• 벡터의 뺼셈

  자기 자신과 크기는 같고 방향이 정반대인 음벡터의 정의를 이용하면 됨

  식 r = a - b의 양쪽에 b를 더한 후 결합법칙과 교환법칙을 적용하여 연산의 순서를 정리하면 식 a = b + r 을 얻을 수 있음

- 벡터의 연산2

• 벡터의 곱셈

  내적(內積) (inner product) (·) (Result : Scarlar)

  외적(外積) (outer product) (X) (Result : Vector)

  • 벡터의 내적(1)

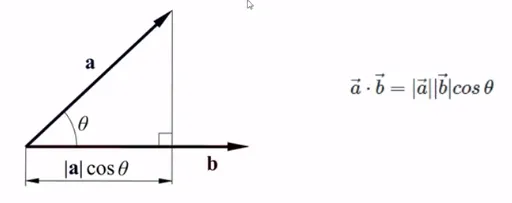
  내적은 벡터를 마치 수처럼 곱하는 개념임

  벡터에는 방향이 있으므로, 방향이 일치하는 만큼만 곱함
  예를 들어, 두 벡터의 방향이 같으면, 두 벡터의 크기를 그냥 곱함

  두 벡터가 이루는 각이 90도 일 땐, 일치하는 정도가 전혀 없기 떄문에 내적의 값은 0

  내적은 한 벡터를 다른 벡터로 투영(Projection), 정사영 시켜서, 그 벡터의 크기를 곱함

• 벡터의 내적(2)

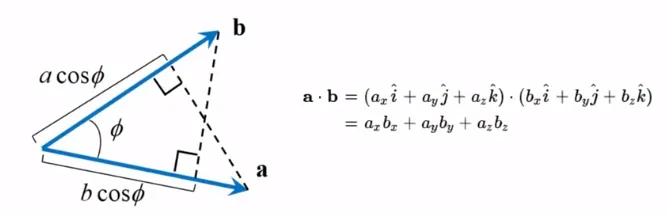
  단위 벡터인 i햇, j햇, k햇은 곱셈에 사용되지 않고 스칼라 값들만으로 계산을 하게 됨

  Sclar 곱은 한 벡터의 크기에 그 벡터에 투영된 다른 벡터의 크기를 곱한 양으로 간주함

  a · b = (a cos∅)b = a(b cos ∅)

  a · b = b · a (Scalar 곱은 교환법칙을 만족함)

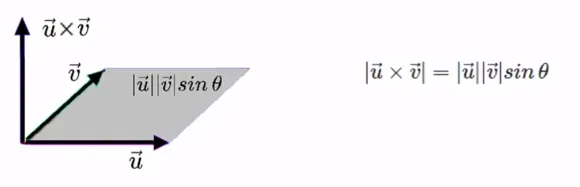
• 벡터의 외적(1)

  두 벡터를 곱하는 또 다른 정의로 외적이 있음

  외적의 결과 값은 벡터인데, 방향은 두 벡터 a와 b가 이루는 평면에 수직임

  r = uv sin∅

  u X v = -v X u

• 벡터의 외적(2)

  직각좌표계에서 단위벡터들은 서로 수직하므로, 서로 다른 단위벡터들의 벡터곱은 크기가 1이고 나머지 단위벡터에 나란한 방향임

  벡터곱과 좌표축의 양의 방향들이 모두 오른손 규칙을 따르므로, 벡터 곱을 취하면 아래와 같음

  자기 자신과의 벡터곱은 사이각이 0이므로 모두 0임

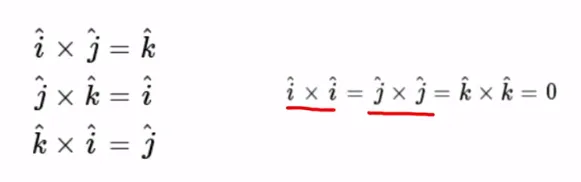
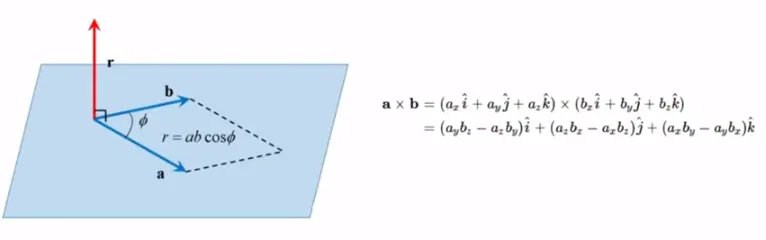
• 벡터의 외적(3)

  두 벡터를 곱하는 또 다른 정의로 외적이 있음

  외적의 결과 값은 벡터인데, 방향은 두 벡터 a와 b가 이루는 평면에 수직임

  r = uv sin∅

  u X v = -v X u

챕터02. 행렬

- 행렬의 정의

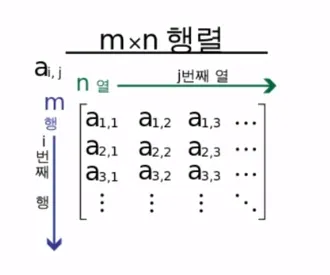
• 행렬의 정의

  행렬을 이용하면 복잡한 자료를 이용한 어려운 계산도 쉽게 풀 수 있고 해석도 직관적으로 가능

  m x n 행렬은 각 행 i ∈ {1, …, m} 및 열 j ∈ {1, …, n}의 순서쌍 {i, j}으로 이루어짐

  각 A_ij를 A의 i번째 행 j번째 열의 성분 (entry) 또는 원소 (element) 또는 계수 (coefficient)라고 함

  A의 각 성분은 행과 열의 번쨰수를 첨수로 사용하여 A_ij, A_i,j, a_ij, a_i,j, A(i, j), A[i, j]으로 표현함

  A_ii (i∈{1, …, min{mn})을 A의 대각성분 (diagonal entry) 또는 대각원소 (diagonal element) 또는 대각요소 또는 주대각선 성분이라고 함

• 행렬의 정의(2)

  행렬 A의 크기는 행과 열의 수의 순서쌍 (m, n) 또는 m x n 을 뜻함

  만약 행과 열의 수가 같다면 (m=n), A를 정사각형행렬(Square matrix) 또는 정방행렬이라고 함

  만약 m = 1이라면, A를 1 x n 행 벡터 (Row vector)라고 표기함

  만약 n = 1이라면, A를 m x 1 열 벡터 (Column vector)라고 표기함

  A = (a_mn) = (m, n) 행렬

  

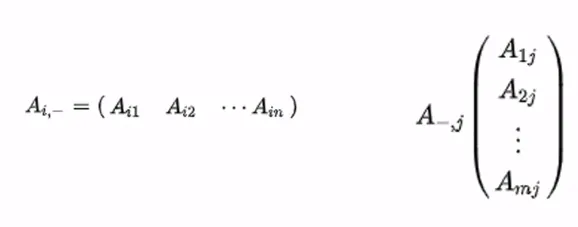
- 행렬의 계산

• 행렬의 계산(1)

  행렬의 더하기와 뺴기는 간단함

  위치가 같은 원소들끼리 더해줌 : 단 행렬의 크기가 동일 해야함

  행렬 A의 상수배 kA는 행렬 A의 각 성분에 임의의 실수 k를 곱함

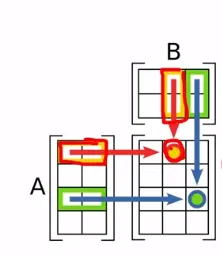
  행렬의 곱하기는 앞의 행렬의 열의 수와 곱해지는 뒤의 행렬의 행의 수가 같을 때만 곱셈이 가능

  또한 곱셈 결과 나오는 행렬의 크기는 앞의 행렬의 행의 수와 뒤의 행렬의 열의 수로 나옴

  마치 백터의 내적 (A와 B의 크기, 스칼라)

  행렬의 곱하기는 AB ≠ BA

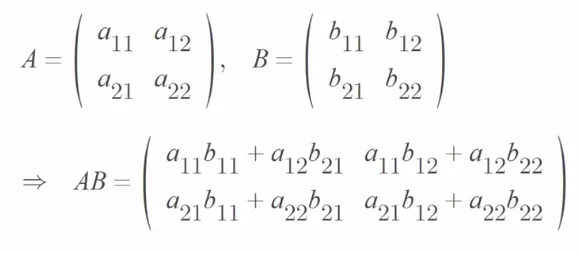
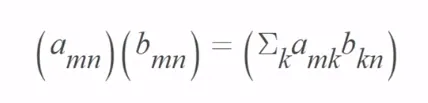
• 행렬의 계산(2)

  앞의 행렬 크기 [m x n] 뒤 행렬 크기 [n x k]이면 두 행렬을 곱했을 떄 [m x k]

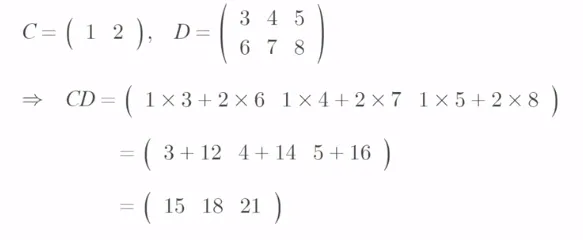
• 전치행렬

  행렬을 뒤집어 놓은 형태

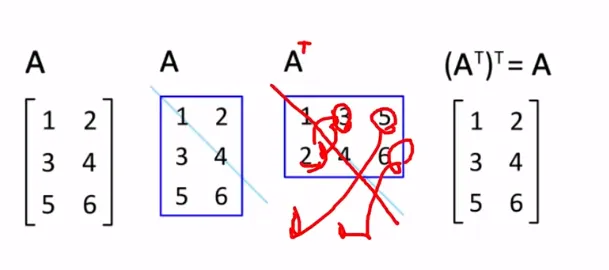
• 역행렬

  2x2는 외울 수 있지만 3x3부터 계산이 무척 복잡해진다

  따라서 데이터 분석 시 시간이 오래 걸리게 된다

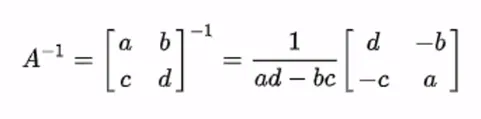
- 기타 특수 행렬

• 단위행렬

  1_nm = diag (1, 1, 1, …, 1)

  1_mmA = A1_nn = A

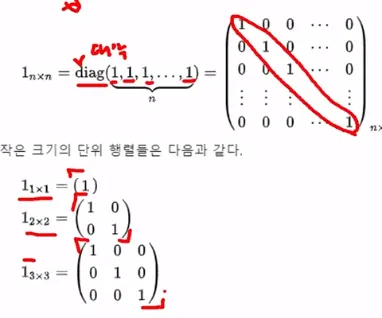
• 대각행렬

  diag(d1, …, d_n)

  diag_mn(d_1, …, d_min(m,n)

  

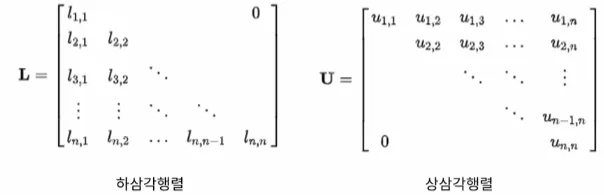
• 삼각행렬

  소거법이나 선형대수할 때 많이 사용

• 대칭행렬

  A = A^T
  즉, A_ij = A_ji

  A = 1/2(A + A^T) + 1/2(A - A^T)

  예시
  ( 1 2 4 )
  ( 2 3 5 )
  ( 4 5 6 )

• 반대칭행렬

  A^T = -A
  즉, 임의의 1 ≤ i, j ≤ n에 대하여,
  a_ji = -a_ij

  예시
  ( 0 2 -1 )
  ( -2 0 -4 )
  ( 1 4 0 )

챕터03. 선형대수학

- 선형 방정식 소개

• 선형 방정식 : linear equation

  a_1 x_1 + a_2 x_2 + … + a_n * x_n = b

  • 비선형 방정식 : nonlinear equation

  4x_1 - 5x_2 = x_1 * x_2
  x_2 = 2 root(x_2) - 6

  • 선형 방정식의 계 : A system of linear equation

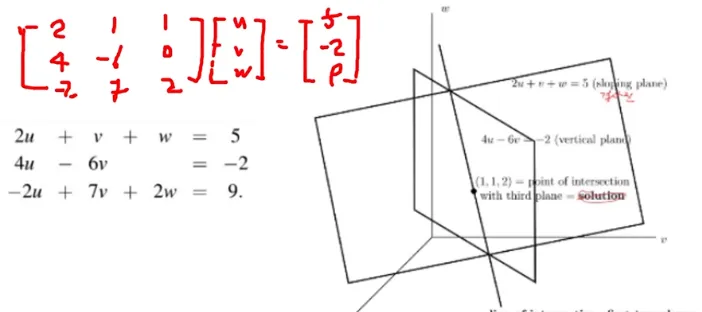
  선형 방정식 계는 선형 시스템 (linear system)이라는 용어를 사용함

  선형 방정식 계는 같은 변수들을 포함한 선형 방정식이 1개 또는 그 이상의 집합을 의미함

  아래 두 개의 선형 방정식은 선형 방정식 계라고 할 수 있음

  2x_1 - x_2 + 1.5x_3 = 8
  x_1             - 4x_3 = -7

  ( 2 -1 1.5 ) ( x_1 )    ( 8 )
  ( 1   0   4 ) ( x_2 ) = ( -7 )
                 ( x_3 )

• 해의 집합 (Solution set)

  Solution set은 선형 시스템에서 모든 가능한 해의 집합을 의미함

• 상등 (Equivalent)

  두 선형 시스템이 같은 solution set을 갖고 있다면 두 선형 시스템은 상등 (equivalent)하다고 함

  즉, 같은 solution set을 갖는 선형방정식 간의 관계를 행 상등 (equivalent)라고 함

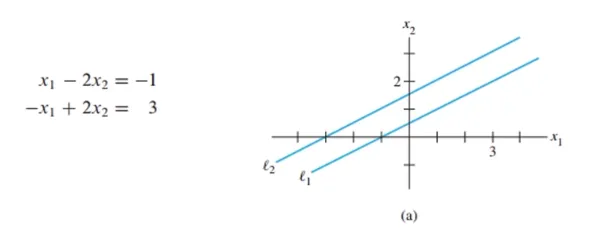
• 해가 없다 (inconsistent)

  inconsistent는 no solution을 의미함

  아래처럼 두 직선이 평행하게 되면 교차점이 없음

  이 경우에 no solution(해가 없다)이며, 두 방정식은 in consistent라고 함

• 해가 있다 (consistent)

  해가 하나인 경우 (exactly one solution)

  해가 무수히 많은 경우

  • 선형 방정식 계 종류 (행의 관점)

  선형 방정식 계는 1. no solution, 2. exactly one solution, 3. infinitely many solution

  inconsistent : 1. no solution을 의미함

  consistent : 2. exactly one solution, 3. infinitely many solution을 의미함

  2개의 해가 존재하는 경우? → 비선형인 경우

• 행렬 표기법 (matrix notation)

  행렬 보기법은 선형 시스템을 행렬로 표현한 것임

  x_1   - 2x_2 + x_3 = 0
           2x_2 - 8x_3 = 8
  5x_1          - 5x_3 = 10

  계수 행렬 (coefficient matrix)
  계수 행렬은 b를 제외하고 a만을 행렬로 나타낸 것

  ( 1 -2 1 )
  ( 0 2 -8 )
  ( 5 0 -5 )

  첨가 행렬 (augmented matrix)
  첨가 행렬은 b까지 포함한 행렬

  ( 1 -2 1 0 )
  ( 0 2 -8 8 )
  ( 5 0 -5 10 )

- 소거법(Elimination)

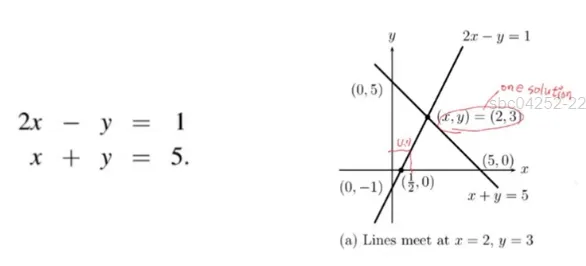
• 선형방정식의 n = 2일 때 행관점, n = 3일 떄 열관점

  행(rows) 관점으로 선형 방정식 접근

  두 개의 식이 X, Y 좌표에 표시할 수 있고 두 식이 교차하는 (2, 3)에서 해(solution)이 존재함

  x = 2, y = 3

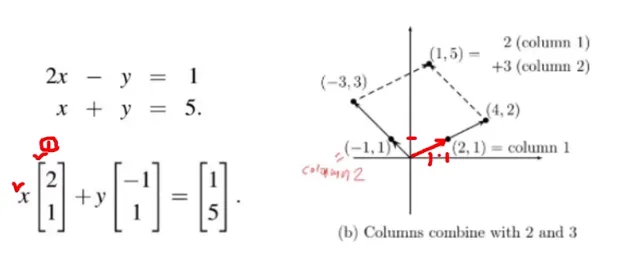
• 선형방정식의 n = 2일 때 열관점, n = 3일 때 열관점

  열(column) 관점으로 선형 방정식 접근

  (2, 1) vector에 2(x)를 곱하고 (-1, 1) vector에 3(y)을 곱함

  위와 같이 곱하게 되면 (4, 2) + (-3, 3) = (1, 5)가 됨

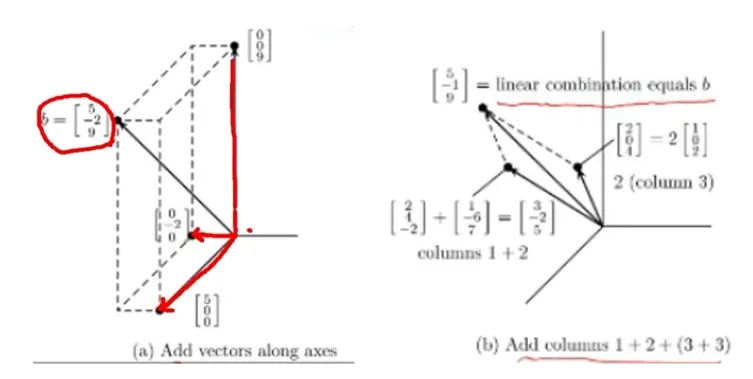
• 선형방정식의 n = 3일 때

  Row picture (행관점) : 평면들의 교차점 (intersection of plans)

  Column picture (열관점) : 열들의 집합 (combination of columns)

• 소거법

  행 연산(row operation)을 통해 소거법을 진행하고 선형 방정식의 해를 구할 수 있음

  가우스 소거법에서 행할 수 있는 기본 행 연산(elementary row operations)은 다음과 같음

  1. 0이 아닌 상수를 행에 곱할 수 있다. (scaling)
  2. 두 행을 교환할 수 있다. (interchange)
  3. 한 행을 상수배하여 다른 행에 더할 수 있다. (replacement)

  상/하 삼각행렬을 만들어 해를 찾음

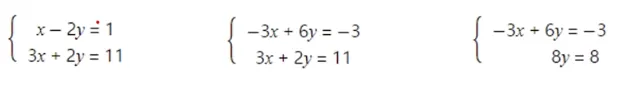
• 가우스 소거법 1단계

  1. 선형 방정식 계를 행렬로 표현함 (첨가행렬)

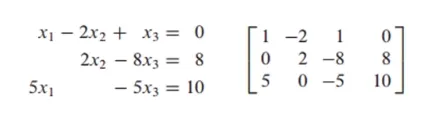
• 가우스 소거법 2단계

  2. 마지막 행의 x_1의 계수를 0으로 만듦

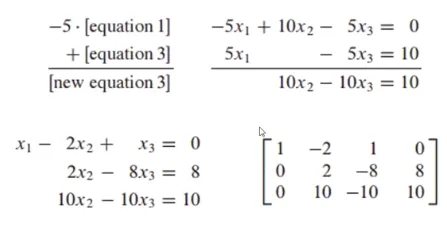
• 가우스 소거법 3단계

  3. 마지막 행의 x_2의 계수를 0으로 만듦

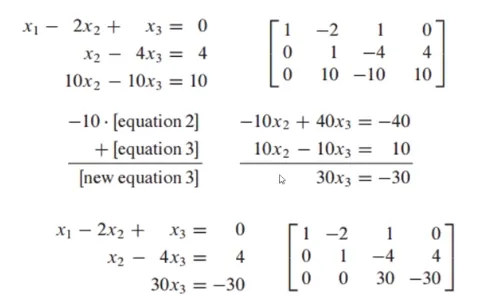
• 가우스 소거법 4단계

  4. 마지막 행의 x_3의 계수를 1으로 만듦
     상삼각행렬 완성

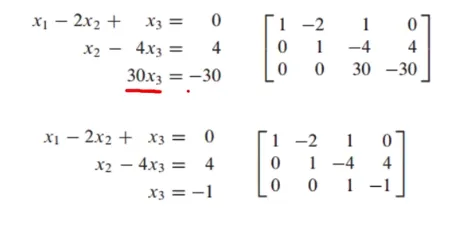
• 가우스 소거법 5단계

  5. x_3을 알았으므로 대입을 통해 x_1, x_2를 구할 수 있음

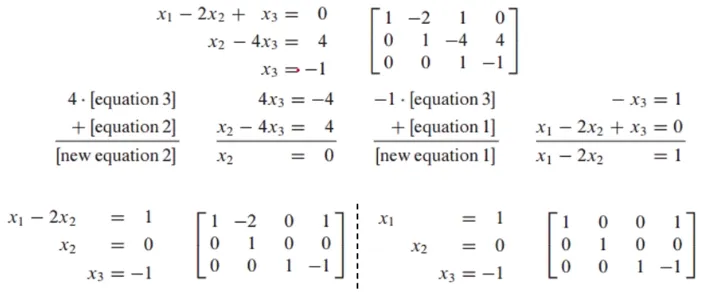
• 행렬이 커지면

  어떤 것을 먼저 뺴줘야 할지 어려워진다
  pivot을 통해 해결할 수 있다 (optimization)

• 행 상등

  행 연산 과정이 하나의 행렬을 다른 행렬로 변환된다면 두 행렬은 행 상등(row equivalent)하다고 할 수 있음

  두 선형 시스템이 행 상등하다면 두 시스템은 동일한 해의 집합을 가지고 있음

- 선형 방정식의 특이한 경우

• 특이한 경우 (The Singular case) 1

  해가 없는 경우 (no solution)
  평행한 직선이 두 개 이상 있으면
  예시엔 3 직선을 만족하는 해가 없다

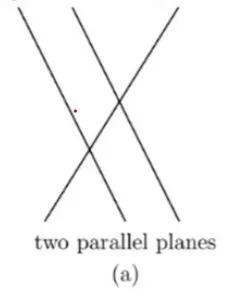
• 특이한 경우 (The Singular case) 2

  세 개의 평면이 평행하지 않는 경우
  평행하지 않더라도 intersection이 없다

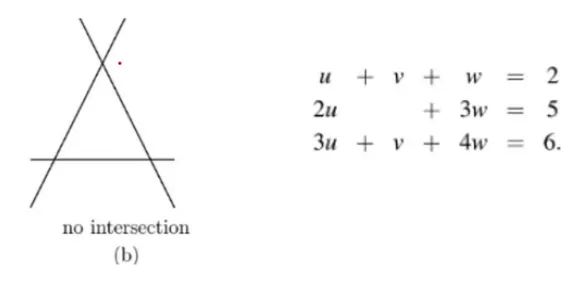
• 특이한 경우 (The Singular case) 3

  해가 무수히 많은 경우 (infinity of solution)
  위에서 본 경우와 옆에서 본 경우
  한 축에 모여 있다

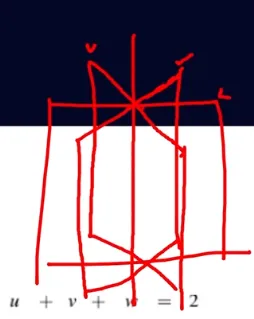
• 시스템이 특이할 때 1 column picture

  위에서는 특이한 경우를 해가 없거나 해가 무수히 많을 떄를 배웠음

  특이한 경우일 떄 column picture에서 어떻게 그려지는지 알아봄

  1. 해가 없는 경우 (no solution) : 세 개의 column이 동일한 평면에 놓이고 b는 다른 평면에 위치할 떄 해가 없음

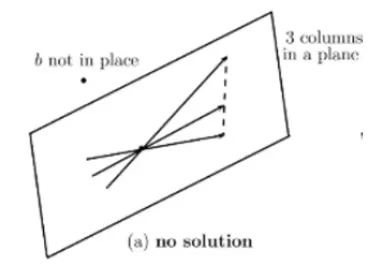
• 시스템이 특이할 떄 2

  해가 무수히 많은 경우 (infinitely many solutions) : b가 3개의 열들과 동일한 평면에 놓여져 있을 때 b를 만들기 위해 3개의 열들은 무수히 많은 방법으로 결합될 수 있음

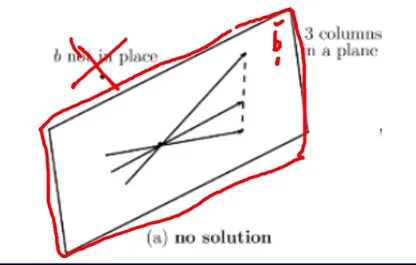
- 역행렬

• 역행렬

  역행렬이 존재하는 행렬 - Invertible Matrix
  2X2 행렬의 결정자(det = ad-bc) - Determinant
  기본행렬 - Elementary Matrix
  A^-1를 찾는 알고리즘 - Algorithm for finding A^-1

• 1. 숫자의 승수 역수 - Multiplicative inverse of a number

  역행렬을 알아보기 전에 숫자의 승수 역수를 알아봄
  5 의 역수는 1/5임

• 2.역행렬이 존재하는 행렬 - Invertible Matrix

  Invertible의 첫 번째 조건은 Row와 Column의 size가 동일해야 함
  AC = I인 C행렬이 있어야 하며 C는 유일(unique) 해야함
  C대신 A^-1로 표기함
  Matrix가 not invertible이면 singular matrix (해가 존재하지 않는 행렬)임 = 역행렬이 존재하지 않으면 해가 없다
  invertible이면 nonsingular matrix(해가 존재)함

• 3.이론 - Theorem 4

  A가 2x2 행렬일 때 ad-bc ≠0이면 A는 invertible함
  ad-bc = 0이면 not invertible임
  여기서 ad-bc는 pivot position이 2개 있을 조건을 의미하며 determinant(결정자)라고 불림
  어떤 matrix가 invertible을 판단할 때 determinant가 0인지 아닌지를 확인해야 함

  A = [ a b ]
        [ c d ]

  A^-1
  = 1/ad-bc [ d -b ]
                 [ -c a ]

• 4.이론 - Theorem 5

  A가 invertible [nxn] matrix이면 R^n 공간에 있는 b에 대한 방정식 Ax = b는 유일한 해를 가짐
  x = A^-1 * b
  A의 inverse를 이용하면 쉽게 solution을 구할 수 있음

  Au = b 이면 u = A^-1 * b
  여기서 u는 x_1과 x_2, b는 k_1, k_2

• 5.이론 - Theorem 6

  A가 invertible matrix이면 A^-1도 invertible임

  (AB)^-1 = B^-1 * A^-1와 동일함
  주의할 점은 순서가 뒤바뀌어 B가 먼저 나온다는 것

  A가 invertible이면 A^T도 invertible
  (A^T)^-1 = (A^-1)^T

• 6.기본행렬 - Elementary Matrix

  기본행렬(elementary matrix)는 항등 행렬(identity matrix)에 단일
  기본 행 연산 (row operation)을 적용해서 얻어짐

  E_1 = [ 1 0 0 ], E_2 = [ 0 1 0 ], E_3 = [ 1 0 0 ], A = [ a b c ]
          [ 0 1 0 ]          [ 1 0 0 ]          [ 0 1 0 ]        [ d e f ]
          [ -4 0 1 ]         [ 0 0 1 ]          [ 0 0 5 ]        [ g h i ]

  E_1은 replacement E_2는 Interchange E_3은 Scaling

  E_1 * A = [  a        b        c     ], E_2*A =  [ d e f ],   E_3*A = [ a   b   c ]
               [ d          e        f     ]              [ a b c ]              [ d   e   f  ]
              [ g-4a   h - 4b   i - 4c ]              [ g h i ]               [ 5g 5h 5i ]

  row operation을 진행하는 것이 기본행렬이다

  [m*n] matrix에 elementary row operation을 수행한다는 것은 어떤 m*m elementary matrix가 존재한다는 의미

  A에 적용한 row operation을 m*m identity matrix에 적용하면 E가 생성됨

  Elementary matrix E가 invertible하면 E의 inverse는 E는 I로 변환하는 elementary matrix임

• 7. A^-1를 찾는 알고리즘 : Algorithm for finding A^-1

  A가 [m*n]이고 invertible이면 항등 행렬 (identity matrix)를 이용해서 A^-1를 찾을 수 있음
  row operation을 계속 해주는 것

• 역선형 변환 - Invertible Linear Transformation

  Linear Transformation이 invertible이라고 불릴 조건은 아래와 같음

  X의 image에 S 함수를 위하면 원래 X로 돌아옴, S함수가 존재하는 경우에는 T는 invertible함

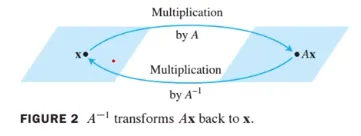
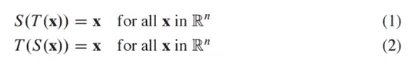
• 이론9

  선형 변환 (linear transformation)은 항상 표준 행렬 (standard matrix)가 존재함

  T가 invertible이면 A(standard matrix)도 invertible함

  또, 선형 변환 S함수는 S(x) = A^-1 * x로 주어짐

- LU 분해 (LU decomposition)

• 분해 - Factorization Decomposition

  분해는 하나의 행렬을 두개 혹은 3개 이상의 행렬 곱으로 표현한 식을 의미함

  A = BC

  A행렬을 B와 C의 곱으로 표현했는데 이런 형태를 분해(factorization)이라고 함

• LU 분해 - LU Decomposition

  방정식을 푸는 방식은 크게 두가지가 있음

  (1) A의 역행렬을 이용

  이 경우에 A^-1 * b_1, A^-1 * b_2 모든 경우를 구해야 하므로 비효율적임

  (2) LU 분해

  행 줄임(row reduction)으로 A를 LU분해하여 방정식을 푸는 것이 효과적

  즉, Ax = b일 때 A를 LU로 나눈 후 Ux를 y로 치환하여 Ly를 통해 b를 구하는 것

  L은 a unit lower triangular matrix (하삼각행렬)
  U는 echelon form (사다리꼴 행렬)

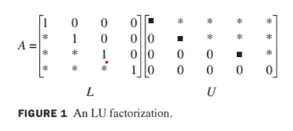
• LU 분해의 유용성

  A = LU로 분해하였을 때 Ax = b 방정식을 다음과 같이 표현할 수 있음

  A = LU → Ax = b → LUx = b → Ux = y(치환) → Ly=b → Ux=y → x의 해를 찾음

  L과 U는 pivot을 사용해서 나머지 entry를 0으로 만들 수 있는 쉬운 형태로 이루어져 있기 때문에 빠르게 문제를 풀 수 있음

• LU 분해 예시 문제

  LUx = b 단계

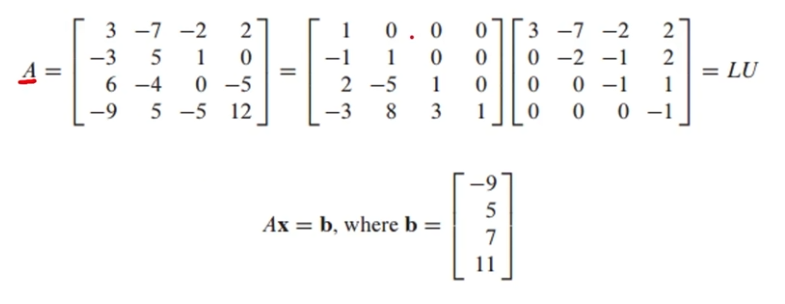
Ux=y(치환) 단계

[L b] = [  1   0   0   0   -9 ]      [ 1  0  0  0  -9 ]  =  [ I  y ]
        [ -1  1   0   0    5  ]  ~   [ 0  1  0  0  -4 ]  
        [  2  -5  1   0    7  ]      [ 0  0  1  0   5 ]
        [ -3   8  3   1   11  ]      [ 0  0  0  1   1 ]

Ly = b → Ux = y → x의 해를 찾는 단계

[ U  y ] = [ 3   -7   -2   2   -9  ]     [ 1  0  0  0   3 ],   x = [  3  ]
           [ 0   -2   -1   2   -4  ] ~   [ 0  1  0  0   4 ]        [  4  ]
           [ 0    0    -1   1    5 ]     [ 0  0  1  0  -6 ]        [ -6  ]
           [ 0    0     0   -1   1 ]     [ 0  0  0  1  -1 ]        [ -1  ]

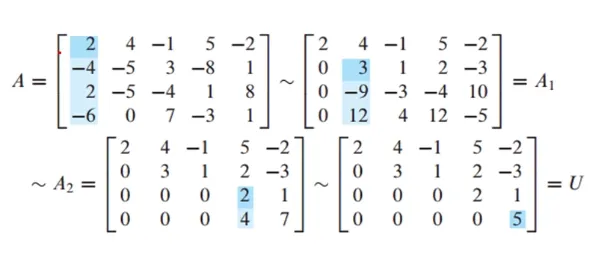
• LU 구하는 방법 - LU decomposition Algorithm

  A가 row replacement만을 사용하여 사다리꼴(echelon form) 형태로 변환될 수 있다고 가정

  U(echelon form)로 변환하기 위해 행 줄임 (row operation) 기본 행렬 E_1, …, E_p가 존재함

  이 기본 행렬의 역행렬(inverse)이 L이 됨 (A가 [m*n]일 때, L은 [m*m], U는 [m*n]이 되어야 함)

  E_p … E_1 * A = U
  A = (E_p … E_1)^-1 * U = LU
  L = (E_p … E_1)^-1

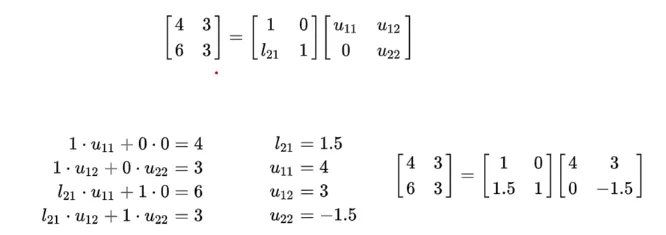
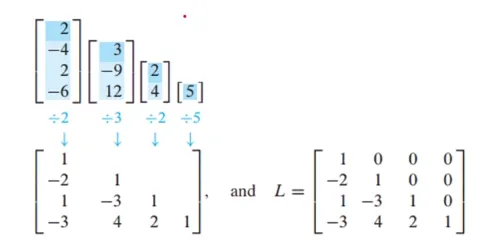
• LU 구하는 방법2

  A가 4개의 행을 갖고 있으므로 L은 4*4가 되어야 함

  L은 A의 각각 pivot column에서 pivot 아래의 entry를 pivot으로 나눠주면 구할 수 있음

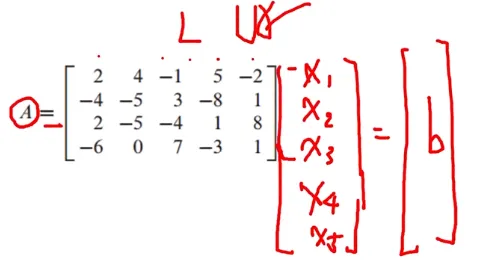
• 수와 관련된 메모 - Numerical Notes

  A^-1로 해를 구했을 때 보다 LU분해의 연산량이 1/3배 적음
  A가 sparse(대부분 0으로 채워져 있는 경우)하면 L과 U로 sparse 함
  하지만 A^-1는 dense(값이 많은 경우)함
  이 의미는 L과 U를 저장하는 memory와 A^-1 값을 저장하는 memory의 차이가 큰 것
  공학적인 문제를 풀 때 LU분해는 속도와 메모리적 측면에서 큰 이점이 있음

  LU분해는 SVD에 자주 사용한다
  Cluster 등 거리 구할 땐 모두 행렬이기 때문에 유용

- 행렬식

• 계수 - Rank, Pivot, Null space

  행렬 A의 Rank는 A의 column space의 dimension을 의미함

  column spac의 basis vector가 몇 개 존재하는지 알면 그것이 dimension이 되는 것

  A를 row reduction을 통해 echelon form(사다리꼴)로 변환하고 pivot column을 찾음

  pivot column이 3개 존재하므로 rank A는 3임

  추가적으로 null space의 dimension은 free variable x_3, x_5 2개 이므로 dim Null A = 2임

  Null space의 dimension은 free variable의 개수와 같음

  만약 x가 5개이면 rank도 5개여야 한다

• 행렬식 - determinant

  2*2행렬에서의 determinant가 nonzero(≠0)이면 invertible임

  3*3 이상 행렬부터는 determinant를 구하는 것이 복잡
  determinant가 0이 아닌 것의 의미는 모든 row에 pivot이 존재한다는 의미
  따라서, row reduction을 진행하고 모든 pivot이 nonzero임을 확인하면 됨
  상삼각행렬 만들고 대각선 모두 곱했을 때 0이 아니면 됨
  대각행렬에 값이 있는 것이 pivot column

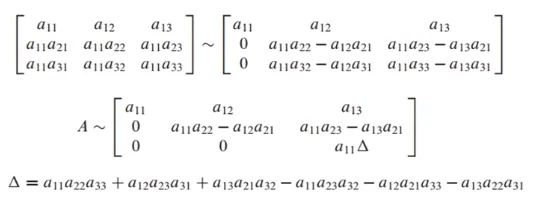
• 행렬식 - determinant 이어서

  Δ = a_11 * detA_11 - a_12 * detA_12 + a_13 * det A_13으로 표현 가능

  A_13은 첫번쨰 row와 3번째 column을 제외한 요소들을 의미
  A가 아래와 같이 주어졌을 때, A_32는 아래와 같이 표기할 수 있음 (3번째 row, 2번째 칼럼 제거)

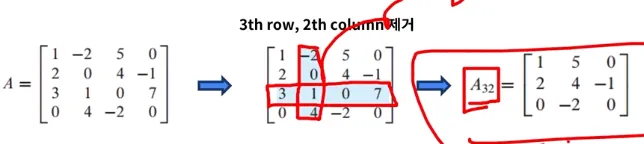
• A 행렬이 주어졌을 때 determinant를 계산하는 예시

• 여인수 - Cofactor

  cofactor를 이용해서 determinant를 여러가지 형태로 표현할 수 있음

  이를 여인수 전개(cofactor expansion)라고 함

• 여인수 (2)

  cofactor expansion을 이용하면 임의의 row와 column으로 determinant를 표현할 수 있음

  임의의 row

  det A = a_i1 * C_i1 + a_i2 * C_i2 + … + a_in * C_in

  임의의 column

  det A = a_1j * C_ij + a_2j * C_2j + … + a_nj * C_nj

  Spare한 row나 column을 선택해서 계산을 빠르게 계산할 수 있음

• det EA = (det E)(det A)

  E는 기본행렬(elementary matrix)를 의미함, det EA는 (det E)(det A)와 동일함

  E_1은 interchange, E_2는 second row k scaling
  E_3은 second row에 k scaling한 것을 first row에 더한 replacement
  E_4는 first row에 k scaling한 것을 second row에 더한 replacement

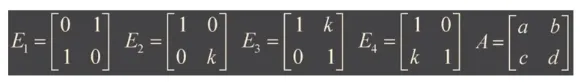
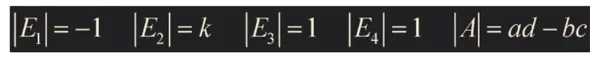
• det EA = (det E)(det A) 증명

• 삼각행렬 행렬식 - Triangular matrix determinant

  A가 삼각행렬이면 det A의 diagonal term을 곱한 것

  det A = a_11 * a_22 * a_33

• 행 연산 - Row Operation

  a. A의 하나의 row 곱이 다른 row에 더해져 B 행렬이 만들어지면 det B = det A임
  이는 row replacement를 의미함

  b. B를 만들기 위해 A의 두개의 row가 interchange 됐으면 det B = -detg A임

  c. A의 하나의 row에 k가 곱해져 B가 만들어졌으면 det B = k * det A 임
  scaling을 의미함

  a, b, c 세가지 성질을 이용하여 row reduction을 통해 사다리꼴(삼각행렬)을 만든 후 cofactor expansion을 이용하면 det를 쉽게 구할 수 있음
  det EA = (det E)(det A)와 det E = 1, -1, k임
  B는 A행렬에 row reduction을 사용하여 만들어진 사다리꼴 행렬이라고 가정하면 B = EA로 표현
  사다리꼴은 triangular matrix이므로 각각의 diagonal term을 곱하면 det를 구할 수 있음

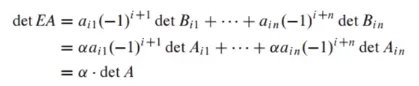
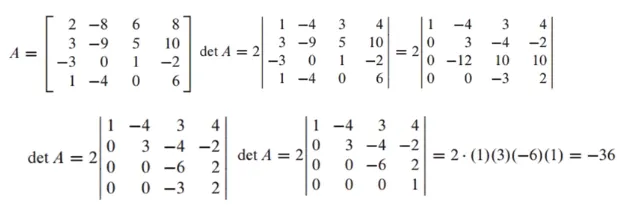
• 행 연산 - Row Operation 수차적인 메모

  cofactor expansion을 사용해서 determinant를 계산하면 n!의 연산이 필요함

  하지만 row operation을 이용하면 2n^3 / 3의 연산이 필요하므로 25*25 이상의 행렬도 빠르게 계산

• 이론(1)

  det A = 0이 아니면 A는 invertible임
  A가 not invertible이면 det A = 0임
  row operation 도중 바로 알아볼 수 있다

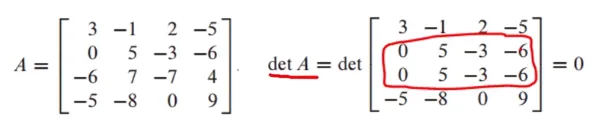
• 이론(2)

  A^T의 det와 det A는 동일함

• 곱셈의 성질 - Multiplicative Property

  det AB = (det A)(det B)
  다만 더한 것은 같지 않다

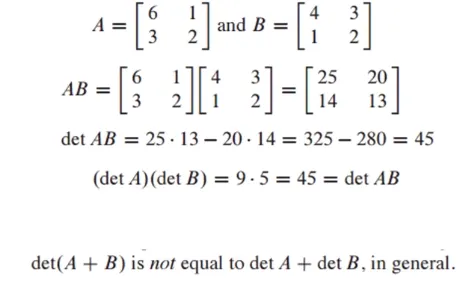
- 고유벡터와 고유값

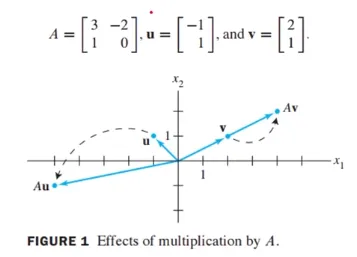
• 고유값과 고유벡터의 기본 idea

  행렬 A, u, v가 다음과 같이 주어졌을 때 곱셈 결과를 시각적으로 표현

  Av의 경과는 동일한 line에 solution이 존재하도록 결과가 도출됨

  이것이 Eigenvalue와 Eigenvector의 기본 idea임

  여기서 Av의 고유값은 2가 되고 고유벡터는 [2 1](세로)이다
  왜내하면 [4 2](세로) = 2[2 1](세로)이니까

• 고유벡터 - Eigenvector

  Ax = λx를 만족하는 nonzero vector x가 eigenvector임

  또한 Ax = λx에서 x가 nontrivial solution(비자명해)이 존재할 때 scalar λ가 eigenvalue가 됨

  여기서 x를 λ에 상응하는 eigenvector라고 함

  nontrivial solution

  free variable (det = 0)를 갖고 있을 때 비자명해를 가지게 됨
  free variable이 없으면 unique solution을 갖고, free variable이 있으면 infinitely many solution을 가짐
  → 평행하면 infinitely many solution → 같은 line상에 존재하는 것 → 고유벡터와 고유값 계산

  행렬 u와 v가 A의 eigenvector인지 판단하는 예시

  Ax = λx를 만족하는 지 확인하면 됨
  u는 A의 eigenvector, -4는 A의 eigenvalue가 됨
  v는 A의 eigenvector가 아님

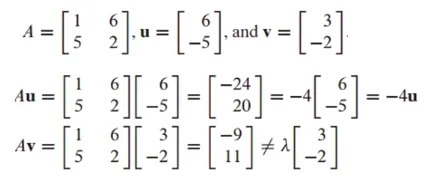
• 고유벡터 (2)

  7이 A의 eigenvalue인지 파악하고 그에 해당하는 eigenvector를 찾는 문제

  x는 nonzero vector가 되어야 하고 이 식이 nontrivial solution이 존재하는지 파악하면 됨
  nontrivial solution을 파악하기 위해 zero vector를 포함한 augmented matrix를 row reduction 후에 free variable이 존재하는지 파악하면 됨
  x_2가 free variable이고 x_2로 표현한 general solution은 아래와 같음
  x_1 = x_2
  nontrivial solution이 존재하므로 7은 A의 eigenvalue가 성립됨

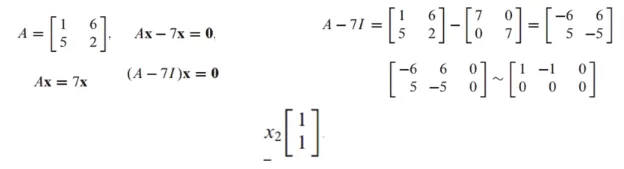
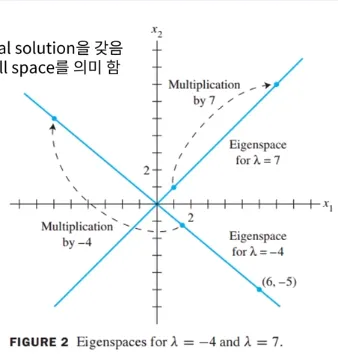
• 고유공간 - Eigenspace

  λ가 A의 eigenvalue이면 (A*(-λ)I)x = 0은 nontrivial solution을 가짐
  λ에 해당하는 A의 eigenspace는 A*(-λ)I 행렬의 null space를 의미함

  eigenspace는 zero vector와 λ에 해당하는 eigenvectors 두가지를 포함함

  zero vector는 eigenvector에 포함되진 않지만, eigenspace에 포함됨

• 고유공간 예시

  행 A가 다음과 같이 주어졌을 때 λ = 2에 해당하는 eigenspace를 찾고 basis를 찾는 예시

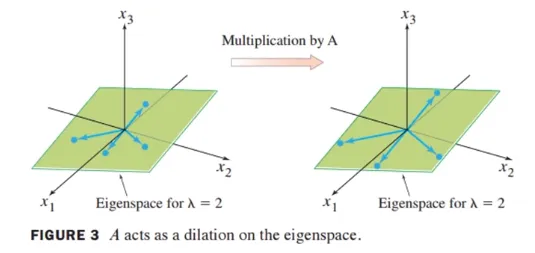
• 행렬 A에 의한 곱셈 - Multiplication by A

  3차원 공간에 λ=2에 대한 eigenspace가 주어졌다고 가정함
  eigenspace는 zero vector와 eigenvectors를 포함함
  eigenspace에 존재하는 임의의 vector 4개를 선택해서 행렬 A를 곱하면 크기가 2배씩 늘어나게 됨

• 이론1

  triangular matrix의 eigenvalues는 diagonal term임

  (1) A가 upper triangular matrix인 경우 A*(-λ)I는 아래와 같음

  아래 방정식에서 nontrivial solution이 존재해야 함
  free variable이 존재한다는 것을 의미하므로 pivot position이 0이 되어야 함
  따라서 λ는 a_11, a_22, a_33이 될 수 있음
  λ의 개수는 n개 이하가 되어야 하므로 3개 이하가 되어야 함

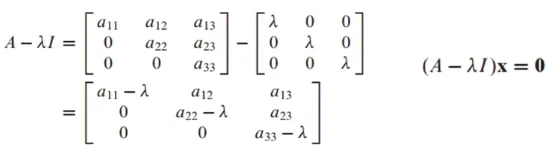
• 이론 1-2

  (2) A가 lower triangular matrix인 경우

  A와 A^T가 동일한 eigen value를 갖고 있다는 것을 증명하면 됨
  λI가 diagonal term만 존재하므로 다음의 식이 성립함

  (A*(-λ)I)^T = A^T * (-λI)^T

  A행렬을 transpose하여도 diagonal term은 변하지 않으므로 A와 A^T가 동일한 eigen value를 가짐

- 특성 방정식

• 특성방정식 - Characteristic equation

  특성방정식은 det (A-λI) = 0을 의미함
  λ가 특성방정식을 만족하면 λ는 행렬 A의 eigenvalue임

  • 특성방정식 예시

  λ(eigenvalue)는 5, 3, 1이 됨
  여기서 eigenvalue 5는 곱(multiplicity) 2를 가짐
  det = a_41 * C_41 + C_42 * C_42 + a_43 * C_43 + a_44 * C_44

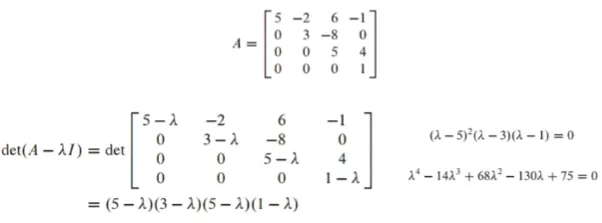
• 유사도 - Similarity

  n차 방정식에서 eigenvalue를 찾는 것은 쉽지 않아 similarity를 주로 사용함
  A = PBP^-1이 성립할 때 A는 B에 similar라고 표현함
  similarity transformation은 A = P^-1*BP로 변환하는 transformation을 의미함

• 이론3

  eigenvalue를 찾을 때 similar한 matrix를 찾아서 eigenvalue를 찾음
  일반적인 경우에 eigenvalue를 구하는 것은 다루기가 어려우므로 특수한 성질을 갖는 matrix의 eigenvalue는 상대적으로 쉽게 구할 수 있음
  A와 B가 similar이고 동일한 특성 polynomial을 갖고 있으면 두 행렬은 동일한 eigenvalue를 가짐
  eigenvalue는 동일하지만 eigen vector space는 보통 다름

• 이론3 증명

  A와 B가 similar이고 동일한 특성 polynomial을 갖고 있으면 두 행렬은 동일한 eigenvalue를 가짐

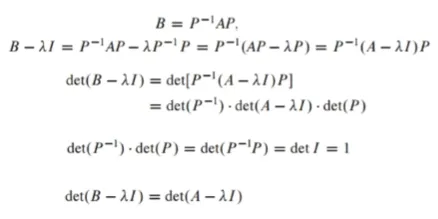
- 대각화(Diagonalization)

• 대각화

  정사각행렬(square matrix) A가 대각행렬(diagonal matrix)와 유사(similar)하면 A를 대각화 가능(diagonalizable)하다고 함
  즉, A = P^-1*DP일 때 A가 diagonalizable이라고 함
  diagonal matrix의 square은 diagonal term의 square임
  만약 A가 D와 similar하면 A^k를 쉽게 구할 수 있음
  대각화는 연산을 대단히 단순하게 만들어준다

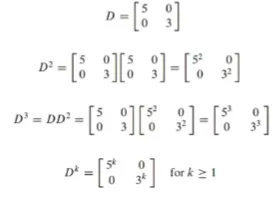
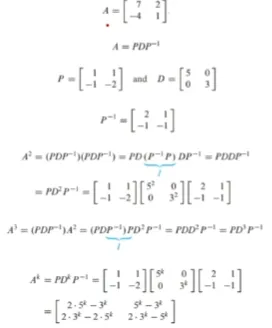
• 이론

  n*n 행렬 A가 diagonalizable이면 A는 n개의 linearly independent eigenvector를 갖고 있음
  즉, D가 diagonal matrix이고 A = PDP^-1이면, P의 column은 A의 n개의 linearly independent eigenvector로 이루어져 있음
  이 경우에 D의 diagonal entries는 P를 구성하는 eigenvector 각각에 대한 A의 eigenvalues임
  p가 v_1, …, v_n로 이루어진 행렬이고 D가 eigenvalues를 diagonal entries로 갖고 있는 diagonal matrix이면 아래와 같음
  P가 invertible이므로 A = PDP^-1이 성립됨

• 행렬 대각화하기 -Diagonalizing Matrices

  (1) 첫 번째로 행렬의 eigenvalues를 찾아야 함

  eigenvalues는 특성 방정식을 이용해서 찾을 수 있음

  0 = det(A*(-λ)I)

  (2) 행렬의 eigenvector를 찾아야함

  λ에 대한 basis를 의미함
  eigenvector를 찾기 위해서는 (A*(-λ)I)x = 0의 general solution을 찾고 eigenvector를 찾고 eigenspace를 찾아서 basis를 찾아야 함
  eigenvector를 찾았으면 n개인지 확인 (n개보다 작으면 대각화 불가능)

  (3) eigenvector로 P를 구성함

  (4) D는 diagonal entries가 eigenvalues인 diagonal matrix임

  위에서 구한 eigenvalues로 D행렬을 구성
  주의할 점으로는 P의 eigenvector에 해당되는 eigenvalue를 diagonal entry로 둬야 함

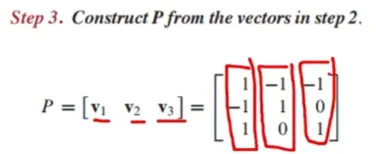
• 행렬 대각화하기 예시

  AP = PD

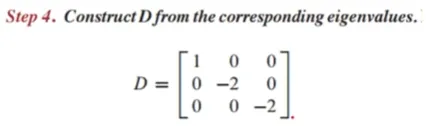
- 대칭행렬의 대각화

• 대칭행렬

  대칭행렬은 행렬 A가 정사각행렬(square matrix)이고, A^T = A를 만족하는 행렬임
  A가 정사각행렬(square matrix)
  A^T = A

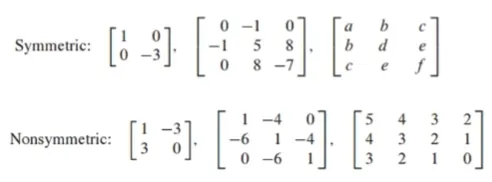
• 대각화 복습

  고유벡터 {v_1, v_2, v_3}는 직교(orthogonal)함
  또한 eigenvector이므로 선형 독립 집합임 (linear independent set)

• 이론1

  대칭행렬의 특성은 A행렬이 대칭행렬이면, 고유벡터는 직교함

  v_1, v_2가 서로 다른 고유치 λ_1, λ_2에 해당하는 고유벡터일 때, v_1 * v_2 = 0의 증명은 아래와 같음

• 이론1 - 직교 대각화 가능 (orthogonally diagonalizable)

  만약 A = PDP^T = PDP^-1이 성립하면 행렬 A는 orthogonally diagonalizable이라고 함
  여기서 P는 정규 직교(orthogonal) 벡터로 이루어진 직교행렬이고, P^T = P ^-1를 성립함
  대칭 행렬은 A^T = A를 만족함
  실제로 A가 orthogonally diagonalizable할 때, A^T = A를 만족하는지 아래와 같이 확인해 봄
  orthogonally diagonalizable이면 A = PDP^T = PDP^-1가 성립

  A^T = (PDP^T)^T = P^TT * D^T * P^T = PDP^T = A

• 이론2 - 직교 대각화 가능 (orthogonally diagonalizable) 예시

  주어진 행렬 A를 orthogonally diagonalization하는 문제
  벡터들과 고유 값으로 P, D행렬을 만들 수 있음

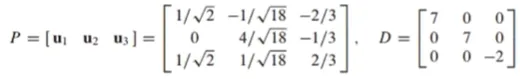
• 이론3 - 스펙트럼 정리 (Spectral Theorem)

  행렬 A의 고유값 집합을 A의 스펙트럼이라고 부름. A가 대칭행렬일 때, 다음과 같은 성질을 따름

  a. A가 n개의 고유치를 갖고 있으면 multiplicity를 계산함
  b. 각 고유치에 해당하는 고유공간의 차원은 고유치의 multiplicity와 동일함
  c. 고유공간은 서로 직교함. 서로 다른 고유치에 해당하는 고유벡터도 직교함
  d. A는 orthogonally diagonalizable함

• 이론3 - 스펙트럼 분해 (Spectral Decomposition)

  스펙트럼 분해는 행렬 A를 eigenvalue(spectrum)으로 표현되는 조각들로 분해하는 것
  행렬 A가 orthogonally diagonalizable하다고 가정하고, 다음과 같이 표현할 수 있음
  A를 위와 같이 표현한 것을 A의 스펙트럼 분해라고 함
  그리고 각 요소 u_k * (u_k)^T는 Rank가 1인 n*n 행렬임

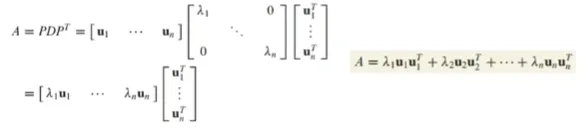
• 스펙트럼 분해 예시

  Orthogonal diagonalizable한 행렬 A를 스펙트럼 분해하는 문제

- 특이값 분해(SVD)

• 특이값 분해 (SVD, Singular Value Decomposition)

  대칭행렬의 대각화에서 배웠던 대각화 이론은 많은 분야에 적용될 수 있음
  하지만, 모든 행렬이 A = PDP^-1로 분해되지 않음
  D가 대각행렬이기 때문에 A는 m*m 행렬이어야지 대각화를 할 수 있음
  특이값 분해 A = QDP^-1는 행렬의 크기 (m*n)와 상관없이 대각화가 가능함

• m*n 행렬의 특이값

  m*n 크기의 행렬 A의 특이값(singular values)는 A^T * A의 고유값(eigenvalue)에 루트를 씌운 값임 그리고 α로 표기함 (델타 수직대칭 모습)
  A^T * A는 n*n 크기의 대각행렬(symmetric matrix)임
  그리고 대각행렬은 대각 요소가 동일하므로 전치를 해도 원래 행렬이 되는 특징과 직교 대각화가 가능함
  A^T * A 행렬을 직교 대각화 한 뒤에, 고유값을 구하고 그 고유값에 루트를 취하면 A행렬의 특이값을 구할 수 있음
  그리고 A의 특이값(singular value)는 Av_1, Av_2, …, Av_n 벡터의 길이이며 A^T * A의 고유값에 루트를 취함
  Ax = λx 였던 것처럼 λ = α, x = Av_1

• m*n 행렬의 특이값 예시

  행렬 A가 주어지고, Ax 길이가 최대가 되는 유닛 벡터 x와 A의 특이값을 찾는 문제

• 특이값 분해(SVD)

  SVD를 배우기 전, 행렬 하나를 정의함
  이 행렬의 크기가 m*n이고, r*r 크기의 대각요소가 특이값인 대각행렬 D를 포함함
  r은 m이나 n을 초과하지 않음
  특이값 분해는 행렬 A를 다음과 같이 분해하는 것 : A = U ∑ V^T
  U는 {Av_1, Av_2, Av_3, …, Av_r}을 정규화한 {u_1, u_2, u_3, …, u_r} 벡터가 열들로 이루어진 행렬이고 A의 left singular vector로 부름
  V는 A^T * A의 정규직교 고유벡터가 열들로 이루어진 행렬이고 right singular vector로 부름.
  V = {v_1, v_2, …, v_n}

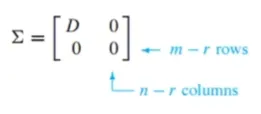
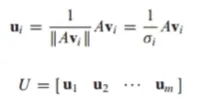
• 특이값 분해 예시

  A^T * A를 직교 대각화하여, 고유값과 정규직교 고유벡터를 찾음
  고유값에 루트를 씌우면 A의 특이값이 되고, 고유벡터로 행렬 V를 만들 수 있음
  U행렬은 Av에 정규화를 한 벡터들이 열을 구성하고 있음

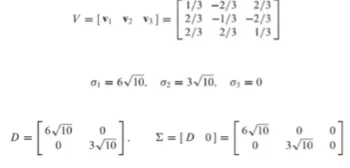
- Reduced SVD, 유사역행렬

• Reduced SVD

  A행렬을 SVD하면 아래와 같음
  위 행렬은 대각행렬인 D를 포함하는데, D행렬은 대각 요소가 특이값(singular value)로 이루어진 r*r 크기의 행렬임. R행, r열까지는 특이값이 이루어져 있고, r+1 행과 r+1 열 부터는 값이 0임
  U와 V가 r+1행, r+1열 부터는 0과 곱해져 0이 되는 것임
  어차피 r을 초과하는 인덱스는 0과 곱해져 0이 되므로 U와 V행렬을 r까지만 표기한 것이 Reduced SVD임

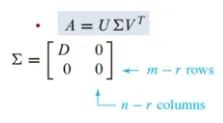
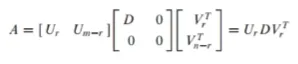
• 유사역행렬 (Pseudo inverse)

  유사역행렬은 A^+를 정의해서 최소제곱법(least-square solution)을 구하는데 이용함

  Ax=b를 풀고자 할 때, x를 다음과 같이 정의함

  x햇의 양변에 A를 곱해 방정식을 풀면 다음과 같이 A는 reduced SVD로 분해한 값을 대입하게 됨

  U_r은 columnA를 span하는 정규직교 기저임. b를 ColumnA에 projection한 것과 동일

  A*x햇은 b를 columnA에 projection한 것이 되고, x햇은 Ax=b의 최소제곱법이 됨

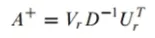
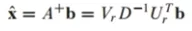
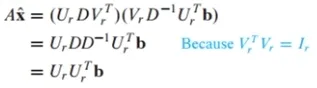
"이 글은 제로베이스 데이터 분석 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다."