교육

제로베이스_데이터분석취업스쿨

강의

머신러닝 기초 챕터01~02
(Regression Problem, Classification Problem)

느낀점

자격증 시험 때 익히 보던 머신러닝들을 배웠다. 자격증 공부를 할 땐 보통 어떤 모델이 어떤 원리로 진행되는 알고리즘이고, 어떤 목적성에 대한 알고리즘이라는 학술적, 원리적인 방식으로 공부를 하였다.
반면 강의에서는 자신의 경험을 녹이며, 어떤 방식으로 주로 사용하는지 예시를 계속해서 들어주면서 설명해주었다. 즉, 실무에서 어떻게 사용되는지 현장성 높은 내용으로 인해 알고리즘에 대한 이해도가 한층 높아지는 것 같았다.
결국, 내가 가장 중요하게 배워야 하는 능력은 '도메인, 목적에 맞게 데이터 분석 능력을 적절하게 활용하는 것'이었다. 즉 '도메인, 목적'을 상정하는 것이 무척 중요하다는 것을 배울 수 있었다.
샘플 프로젝트를 통해 어떤 식으로 진행되는지 배웠다면, 이제 개인 프로젝트를 통해 실제로 분석 목적을 기획하는 작업을 통해, 기획력을 높이고, 그동안 배운 지식을 체화하도록 노력해야겠다고 느꼈다.

수업 내용

챕터01. Regression Problem

- Loss Function & Linear Regression 설명

• 데이터 종류 : 정형 데이터 vs 비정형 데이터

  정형 데이터 : N*P, Table 데이터, Excel Data

  비정형 데이터 : Image, Text, …

  16*16 flatten→ 256 Dimensions

  흑백↔RGB 1채널과 3채널

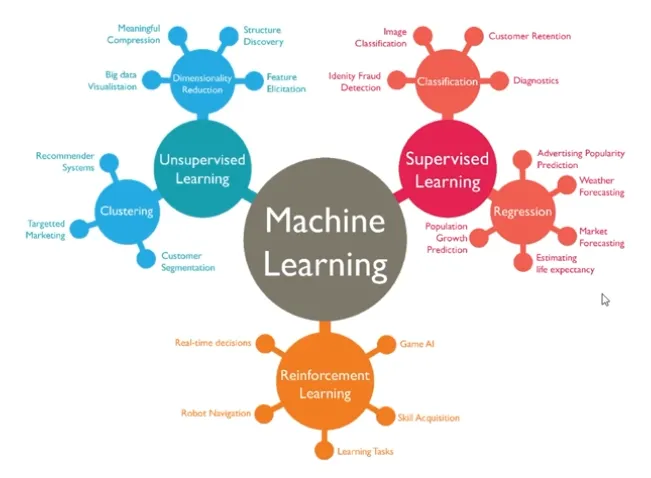
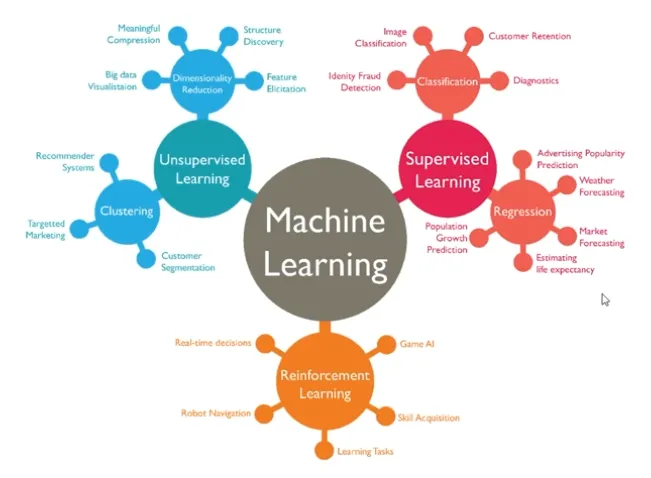
• Machine Learning 종류

• 정형 데이터

  X : Variables, Features, Columns, 독립변수, 설명변수

  Numerical : 연속적인 변수 (2는 1보다 크다, 변수에 대/소가 있음)
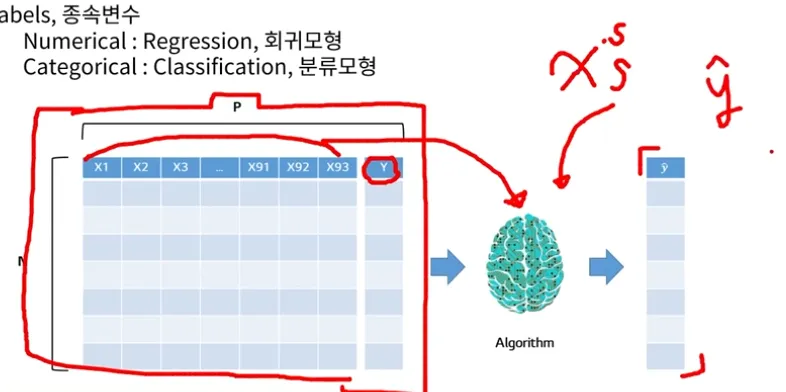
  Categorical : 이분적인 변수 (2는 1과 다름, 변수에 대/소가 없음)

  Y : Lables, 종속변수

  Numerical : Regression, 회귀모형
  Categorical : Classification, 분류모형

  새로운 x들을 바탕으로 예측한 y값을 y햇이라 부른다

• 좋은 알고리즘의 기준?

  Error가 낮은 Algorithm

  Algorithm = Input → Process → Output

  Model
  Set of rules to obtain the expected output from the given unput

• Loss Function

  Error는 True set (Y) - Algorithm output(y_햇)

  Error = ∑((y_햇) - y)^2
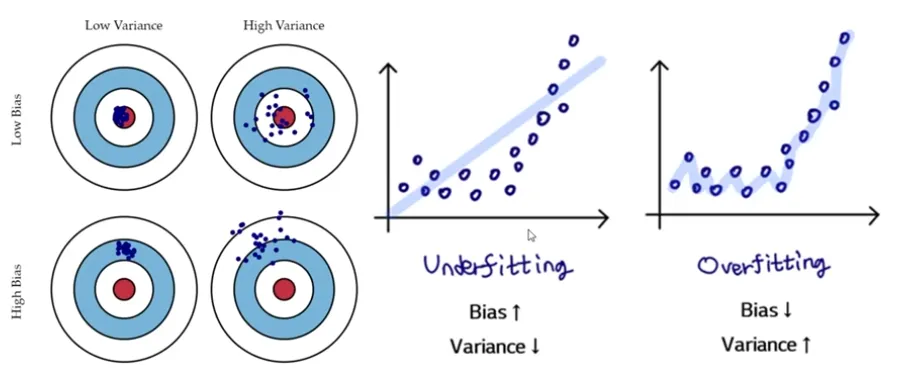
  Error = Variance + Bias
  Variance : 추정값(Algorithm Output)의 평균과 추정값들간의 차이
  Bias : 추정값( Algorithm Output)의 평균과 참값(True)들간의 차이
  Bias는 참값과 추정값의 거리를 의미. Variance는 추정값들의 흩어진 정도를 의미함

  알고리즘에서는 High variance, Low bias를 고치는 것을 더 선호

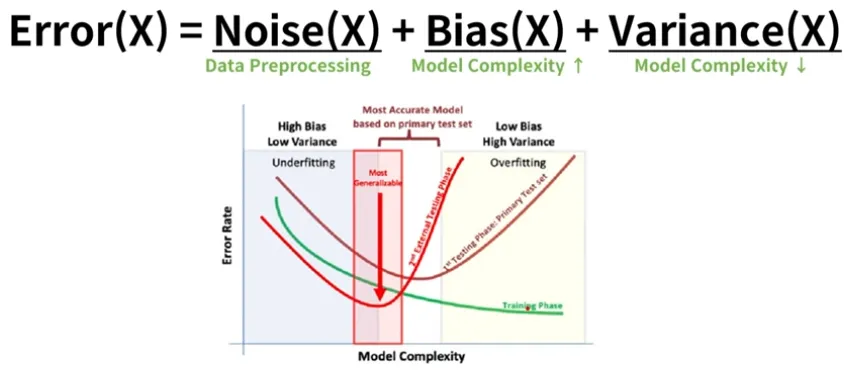
• Error(x) = Noise(x) + Bias(x) + Variance(x)

  Noise를 낮추기 위해 data preprocessing

  Bias를 낮추려면 Model complexity를 높여야 한다
  Variance를 낮추려면 Model Complexity를 낮춰야한다

  Trade off

  Loss Function은 Min Error(x)

• Linear Regression

  Simple Linear Regression
  독립변수 X 1개, 종속변수 Y 1개
  E(y_i) = β_0 + β_1 * x_i

  추정값(DV, Dependent variable) = 상수 (Constant) + Coefficient(계수, x가 1단위 증가했을 때, y에 미치는 영향도)x_i

• Multi Linear Regression

  독립변수 X 2개, 종속변수 Y개

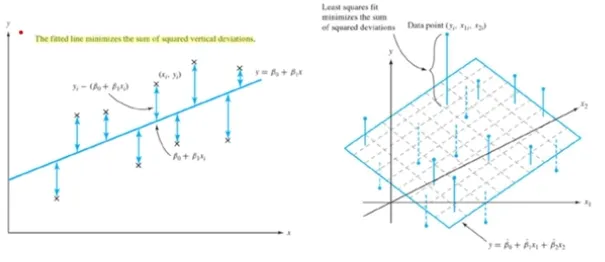
• Square

  추정값과 참값의 차이를 표현하는 방식의 차이
  하지만 제곱(Square)의 장점은 빠르게 문제 해결이 가능
  Closed Form

- β(계수) 추정법

• Simple & Multi-Linear Regression

  에러 최소화

• β 추정법

  각 β에 대해 편미분을 사용하여 추정을 수행함
  Linear Regression의 Loss Function은 Closed Form Quadratic이기 때문에 미분만으로 쉽게 추정 가능
  β가 여러개일 때 똑같이 각 β에 대해 미분 수행 후 추정함

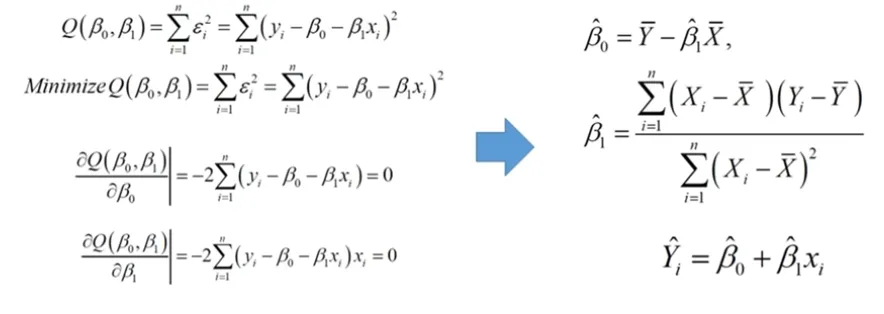
• β 추정법 (2)

  β에 대한 p-value가 낮으면 기울기가 0이 아닌 것으로 판명
  통상적으로 p-value가 0.05이하면 의미 없다고 판단
  (β의 기울기가 0일 확률이 0.05 이하라고 해석함)
  즉, p-value가 0.05 이하면 H_0(귀무가설)은 기각되며 H_1(대립가설)이 채택됨

• 2가지의 Factor를 활용한 Model의 Output 해석

  Factor 1 : β_1 (β_0 제외)

  X가 1단위 증가 시 Y에 영향을 미치는 정도

  β_1이 10인 경우 x_1이 1증가했을 때 Y에 10의 영향을 미침

  β_1의 값이 크면 Y에 영향을 크게 미친다고 판단할 수 있음
  하지만 X’s간 Scale이 다를 수 있기 때문에 X’s간 상대적인 비교는 불가함

  키와 몸무게는 기본적으로 Scale이 다름

  Factor 2 : p-value

  β_1 값이 크지만 p-value 값이 높으면 의미가 없음
  따라서 β_1 값과 p-value값, 두 가지 조건이 맞아야 유의미하다고 판단할 수 있음

  X’s간 중요한 변수를 Ranking하고 싶을 때 다른 방법 : X’s Scaling

- Model 평가 및 지표 해석

• Model의 평가기준

  동일한 평가기준으로 Model의 성능을 평가해야 함

• R-Squared

  Regression Model의 정성적인 적합도 판단
  R^2는 평균으로 예측한 것에 대비 분산을 얼마나 축소시켰는지에 대한 판단
  보통은 아래의 수식과 달리 Correlation(y, y_햇)의 제곱으로 표현함
  정성적인 판단이 필요한 이유는 통상적으로 Model의 예측력을 판단하기 위함
  0~1 사이의 값을 갖고 1에 가까울수록 좋은 모델
  SSE/SST = 1 - (SSR/SST)

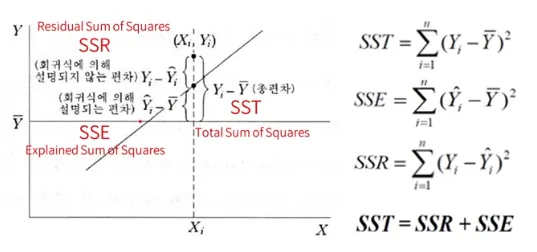
• R^2 어느 정도 수치일 때 쓸만한 모델일까?

  현업에서 R^2가 0.3 이상인 경우를 찾기 힘듦
  R^2의 경우 0.25 정도도 유의미하다고 판단함

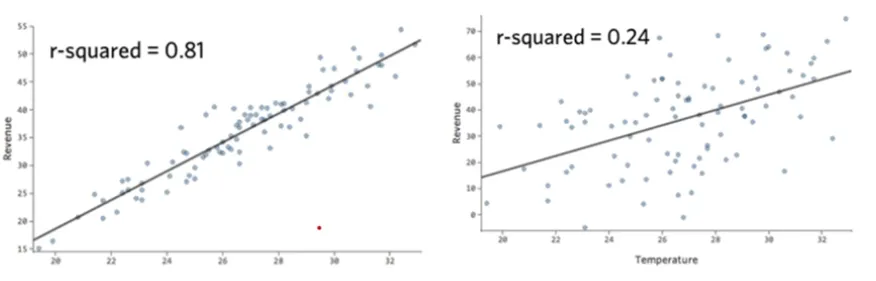
• 성능지표1 : Average Error - 평균오차 (잘못된 정량적인 방법)

  실제값에 비해 과대/과소 추정 여부를 판단
  부호로 인해 잘못된 결론을 내릴 위험이 있음

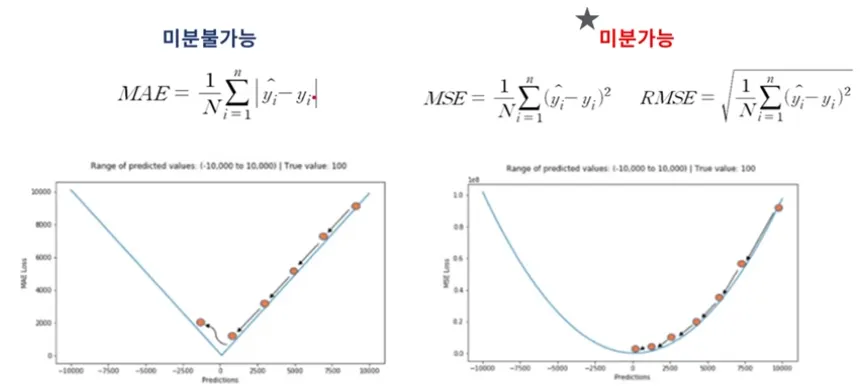
• 성능지표2 : Mean Absolute Error ; MAE - 평균 절대 오차

  실제값과 예측값 사이의 절대적인 오차의 평균을 이용
  미분이 되지 않아서 안쓴다

• 성능지표3 : Mean Absolute Percentage Error ; MAPE - 평균 절대 비율 오차

  실제값 대비 얼마나 예측값이 차이가 있는지를 %로 표현
  상대적인 오차를 추정하는데 주로 사용
  MAPE = 100% * (1/x) ∑ [(|y-y’|) / |y|]

• 성능지표4&5 : (Root) Mean Squared Error ; (R)MSE

  부호의 영향을 제거하기 위해 절대값이 아닌 제곱을 취한 지표

• Model 평가 및 해석 순서

  Model Loss Function은 평가지표로 하는 것이 좋음

  Model 성능 Check : 정성, 정량
  → Model 성능 안나올 시 Data Quality Check

  Model Loss Function은 평가지표로 하는 것이 좋음

  P-value를 확인하여 의미있는 변수 추출

  β_i 활용, X 1단위 증가 당 Y에 얼마만큼 영향을 미치는지 판단

- Feature Selection 기법

• Feature Selection

  Overfitting을 방지하기 위해서 Feature Selection 수행
  Feature의 수가 많아지면 많아질수록 Model Complexity(복잡도)는 높아짐
  Model Complexity가 높아지면 높아질수록 Bias는 낮아지는 반면 Variance가 높아짐
  따라서, Feature Selection을 활용하여 Bias와 Variance의 Trade-off 최적점을 도출해야함

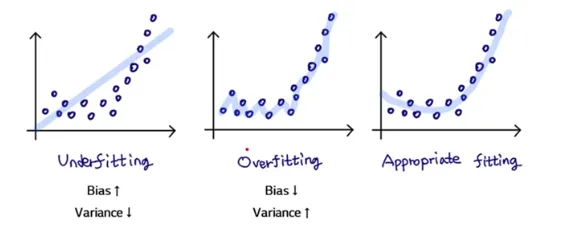
• Supervised Variable Selection - Exhaustive Search (완전 탐색)

  Feature의 좌석 조합을 찾아냄
  경우의 수는 2^p - 1 (단, P는 Feature의 개수)
  총 7개 Subsets의 정확도를 바탕으로 최적의 조합을 찾아냄

  Training Set의 정확도보다 Test Set의 정확도를 봄

  이러한 Exhaustive search (완전 탐색) 방법은 시간이 너무 오래 걸림

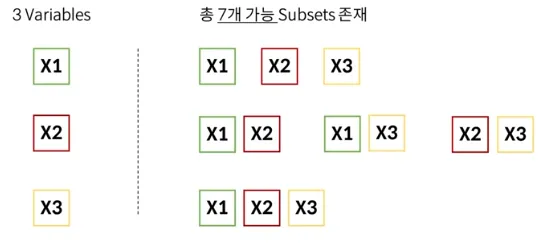
• Supervised Variable Selection - Forward Selection

  Multiple linear Regression에서의 Forward Selection

  처음에는 Variable 없이 시작해서 하나씩 중요한 변수들을 Sequentially 추가함
  한번 선택된 variable은 절대 지우지 않음

  8개 Variables 예시

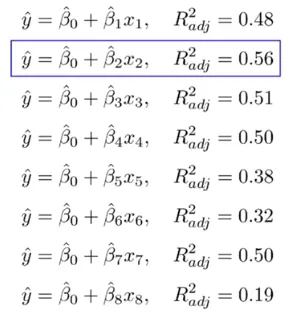
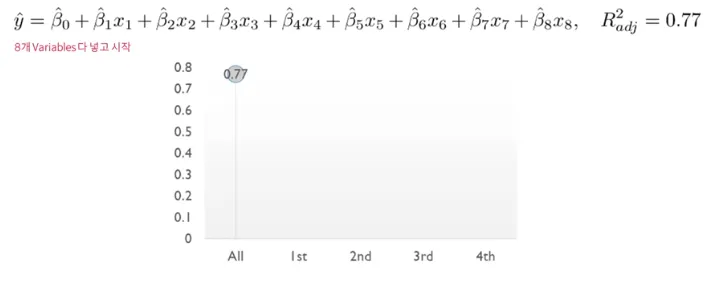
• Supervised Variable Selection - Backward Elimination

  Multiple Linear Regression에서의 Backward Elimination

  처음에는 모든 variables을 사용하고, 정확도에 영향을 미치지 않는 불필요한 variable을 sequentially 제거함
  한번 제거된 variable은 절대 다시 선택하지 않음

  8개 variables 예시

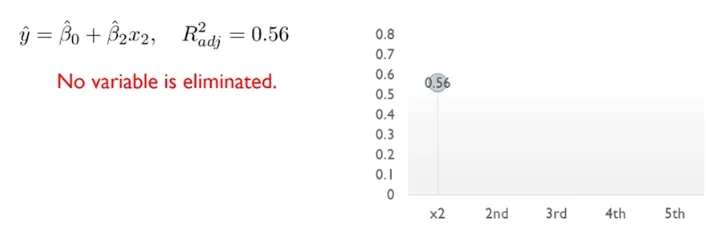
• Supervised Variable Selection - Stepwise Selection

  Forward Selection과 Backward Elimination을 번갈아가며 수행함
  Forward Selection과 Backward Elimination보다 시간은 오래 걸릴 수 있지만, 최적 Variable Subset을 찾을 가능성이 높음

- Pnealty Term

• 전통적인 Feature Selection 방법의 단점

  전통적인 Feature Selection 방법은 Variables가 커짐에 따라 시간이 매우 오래 걸리게 됨
  Forward Selection, Backward Elimination, Stepwise Selection의 경우 최적 Variables Subset을 찾기 어려움
  즉, 가성비가 떨어짐 (Computing Power, Time, Result …)

  Model이 Error를 Minimize하는 과정에서 Feature를 Selection 해줄 수 있는 방법은 없을까?

• Feature Selection 종류

  Filter Method : X’s와 Y의 Correlation, Chi-Square Test, Anova, Variance Inflation Factor 등 간단한 기법으로 Filtering 수행

  Wrapper Method : Forward Selection, Backward Elimination, Stepwise Selection을 활용한 Feature selection

  Embedded Method : Regularization Approach를 활용하여 Model이 스스로 Feature Selection을 진행하는 방법

• Embedded Method 장점

  Wrapper Method와 같이 Features의 상호작용을 고려함
  다른 방법보다 상대적으로 시간을 save할 수 있음
  Model이 Train하면서 Feature의 Subset을 찾아감

• Penalty Term 기본 사상

  Penalty는 축구 경기에서 반칙을 했을 때 부여하는 “벌”의 개념임
  Model에서는 불필요한 Feature에게 “벌”을 부여해서 학습하지 못하게 해야함
  Error를 Minimize하는 제약 조건에서 필요없는 Feature의 β(계수)에 Penalty를 부여함

• Penalty Term 극단적 예시

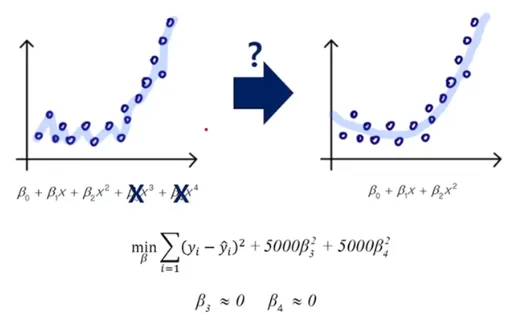
- Regularized Model - Ridge

• Ridge Regression

  β^2에 Penalty Term을 부여하는 방식
  Penalty Term을 추가한 Regularized Model의 경우 Feature 간 Scaling 필수

  λ : regularization parameter that controls the tradeoff between two objectives. 즉, Hyperparameter

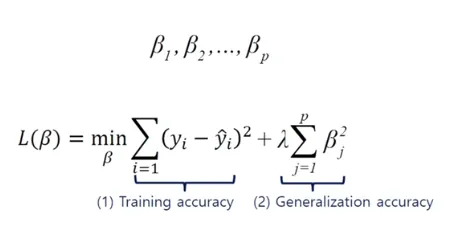
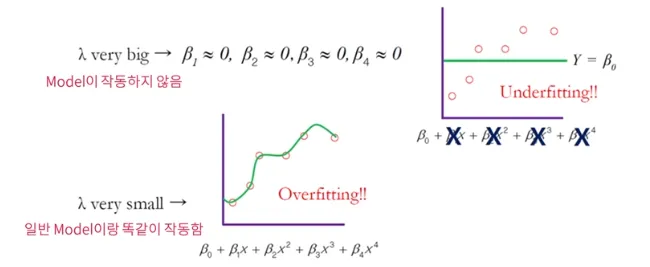
• β^2에 Penalty Term을 부여하는 방식 = L_2-norm = L_2 Regularization

  제곱 오차를 최소화하면서 회귀 계수 β^2을 제한함

• Ridge Regression (2)

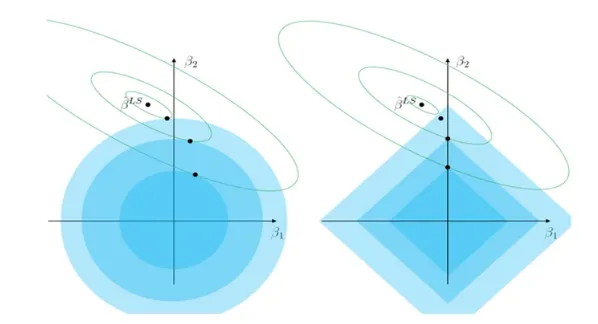
  MSE Contour : 중심에서 멀어질수록 Error 증가

  Train Error를 조금 증가시키는 과정 (Overfitting 방지)

  Ridge Estimator와 MSE Contour가 만나는 점이 제약 조건을 만족하며 Error가 최소가 됨

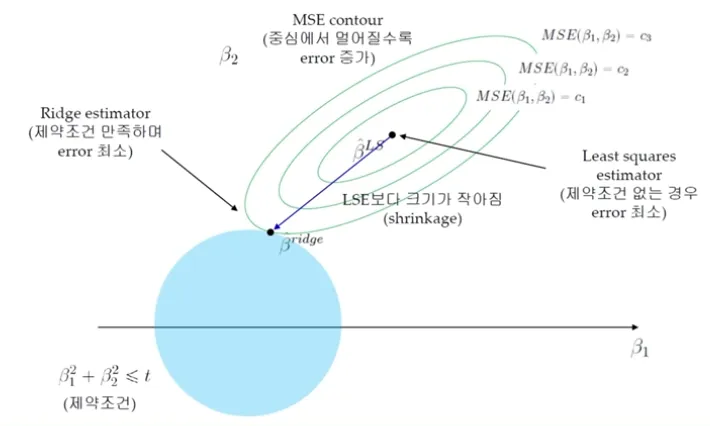
• Ridge Regression (3)

  Ridge는 미분이 가능하기 때문에 Closed Form Solution을 구할 수 있음
  빠르게 해를 찾을 수 있다는 장점

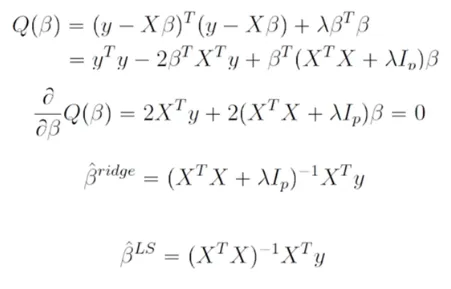
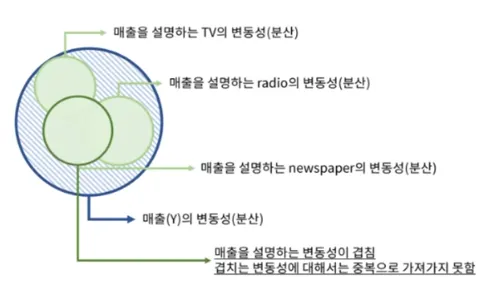
• Ridge Regression 특징

  Ridge는 해 공간에서도 볼 수 있뜻 Feature Selection은 되지 않음
  하지만 불필요한 Feature은 충분히 0에 거의 수렴하게 만들어 버림
  Ridge Regression은 Feature의 크기가 결과에 큰 영향을 미치기 떄문에 Scaling이 중요함
  다중공선성 (Milticollinearity) 방지에 가장 많이 쓰임

- Regularized Model - LASSO

• LASSO Regression

  Least Absolute Shrinkage and Selection Operator
  |β| = L_1-norm = L_1 Regularization에 Penalty Term을 부여하는 방식

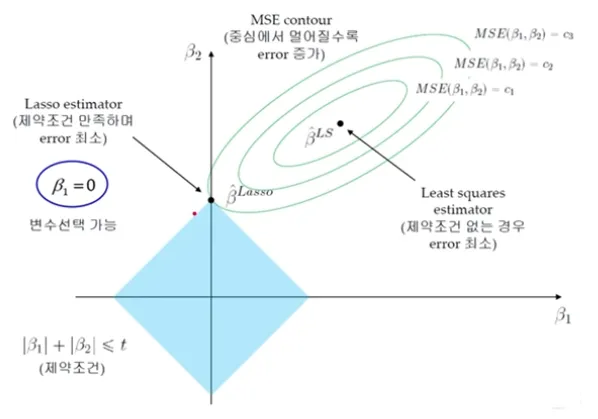
• LASSO Regression (2)

  MSE Contour : 중심에서 멀어질수록 Error 증가
  → Train Error를 조금 증가시키는 과정 (Overfitting 방지)

  LASSO Estimator와 MSE Contour가 만나는 점이 제약조건을 만족하며 Error가 최소가 됨

• LASSO Regression (3)

  Ridge Regression과 달리 Lasso Formulation은 Closed Form Solution을 구하는 것이 불가능

  절대값이기 때문에 미분 불가능

  Numerical Optimization Methods 필요

  Quadratic Programming techniques (1996, Tibshirani)
  LARS Algorithm (20224, Efron et al.)
  Coordinate descent Algorithm (2007, Fridman et al.)
  Semi-differentible

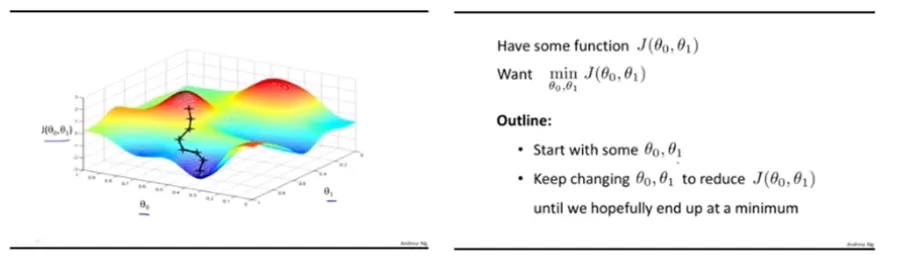
• Lasso Regression (4)

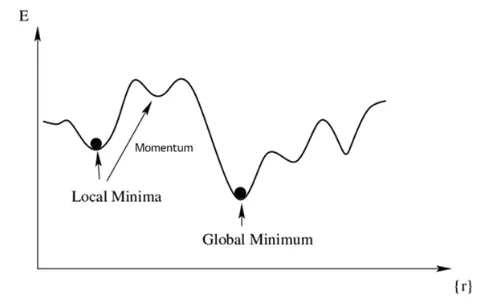
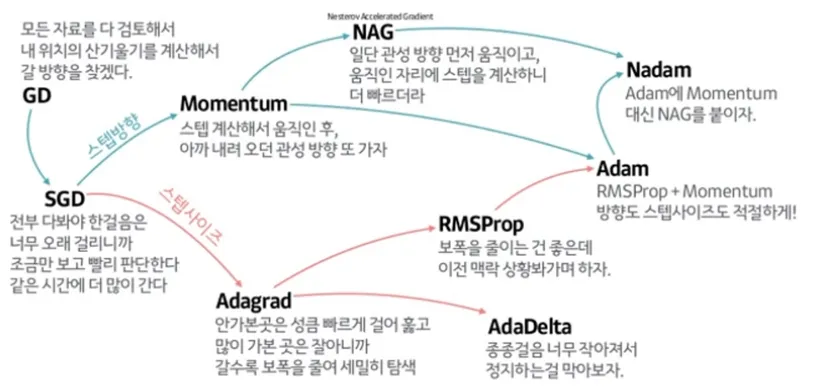
  Gradient Descent : 경사 하강법

  Non-convex 경우 Gradient Descent를 활용하여 해(Loss가 가장 낮은)를 찾아 감

  non-convex → closed form (X) → 미분 (X)
  대부분의 non-linear regression 문제는 closed form solution이 존재하지 않음
  Closed form solution이 존재해도 수많은 parameter가 있을 때 Gradient Descent로 해결하는 것이 효율적
  시작점이 중요하기에 동시에 시작하는 경우가 많다

  Local Minima에 빠질 수 있음
  우리는 Global Minimum이 있는지 알 수 없음

  Global Minimum을 보장하지 않기 때문에 현재까지도 다양한 연구가 이루어지고 있음
  Deep Learning의 Loss Function 최적화 시 매우 중요한 개념 (시작점이 중요, 병렬 처리 가능)

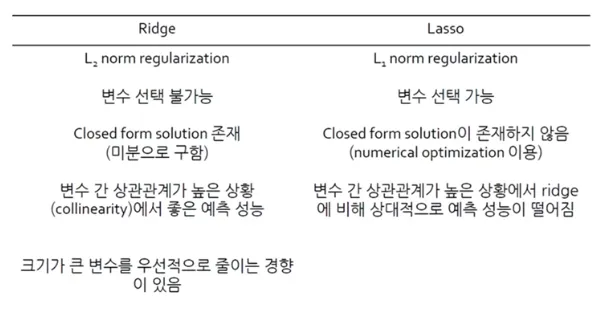
• LASSO Regression

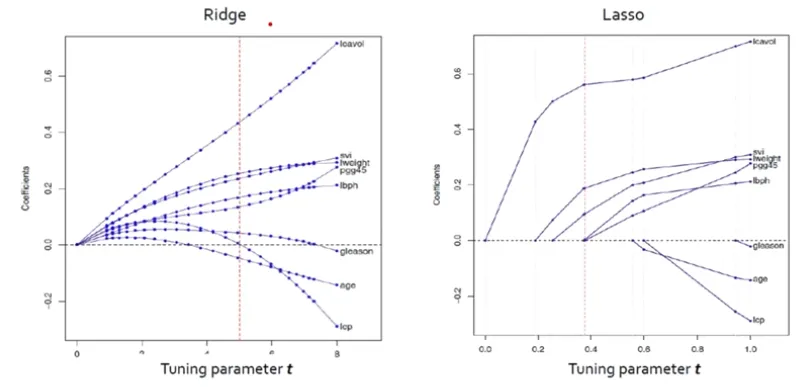
  Ridge와 LASSO 모두 t가 작아짐에 따라 (λ가 커짐에 따라) 모든 계수의 크기가 감소함
  Ridge : 크기가 큰 변수가 더 빠르게 감소하는 경향을 보임
  LASSO : 예측에 중요하지 않은 변수가 더 빠르게 감소, t가 작아짐에 따라 예측에 중요하지 않은 변수는 0이 됨

- Regularized Model - ElasticNet

• Ridge + LASSO = ElasticNet

  Ridge와 LASSO의 장단점은 분명하게 있음
  ElasticNet은 Ridge의 L_2-norm과 LASSO의 L_1-norm을 섞어 놓았음 (두 개의 장점 사용 가능)

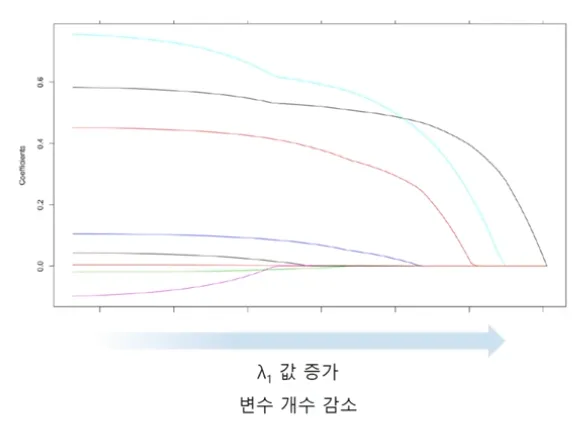
• Ridge + LASSO = ElasticNet (2)

  λ_1 : LASSO Penalty Term (Feature Selection)
  λ_2 : Ridge Penalty Term (다중공선성 방지)

  ElasticNet은 Correlation이 강한 변수를 동시에 선택/배제하는 특징을 갖고 있음

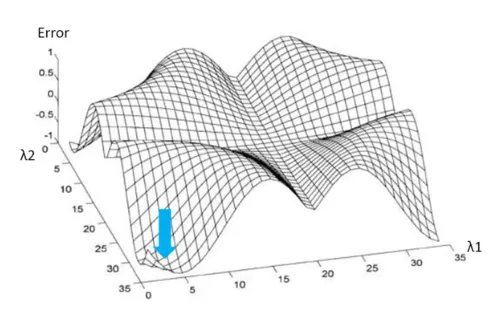
• Ridge + LASSO = ElasticNet (3)

  일정 범위 내로 λ_1, λ_2를 조정하여, 가장 좋은 예측 결과를 보이는 λ_1, λ_2를 선정함
  Ridge, LASSO보다 더 많은 실험이 필요하다는 단점이 존재함
  조절해야하는 파라미터가 2개로 늘어난 것이다

• Ridge + LASSO = ElasticNet (4) 해공간

  마름모와 원 사이가 ElasticNet 경계선

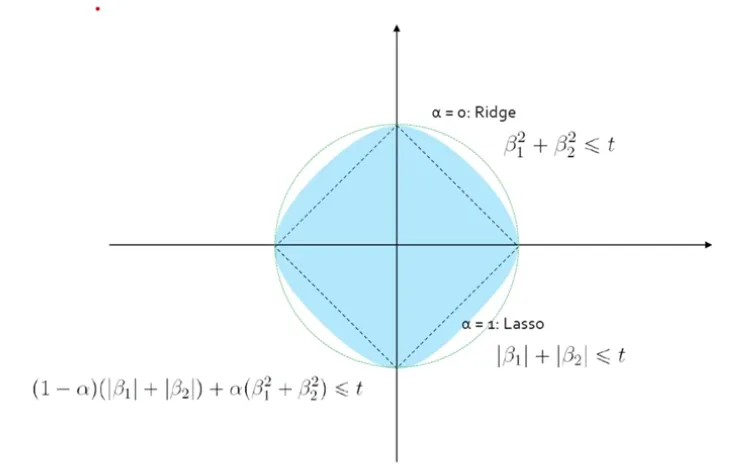
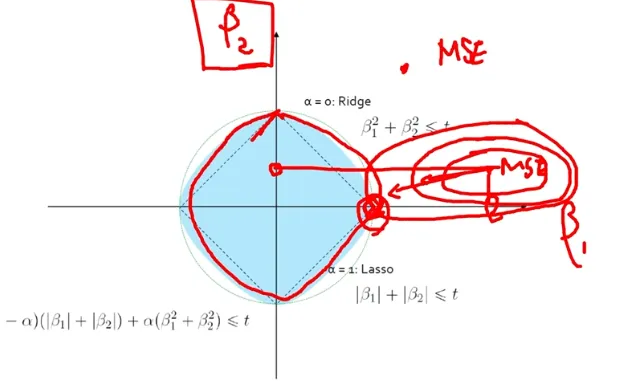
• Ridge + LASSO = ElasticNet (5) Penalty Term

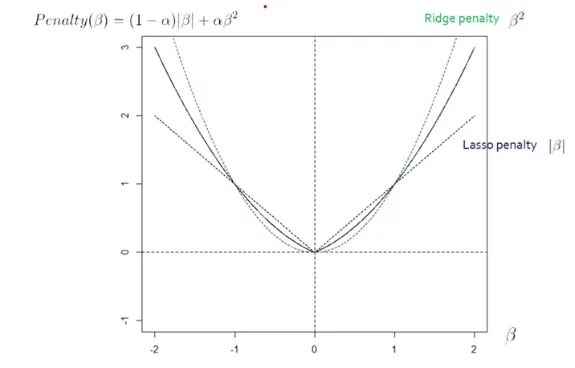
• Ridge, LASSO, ElasticNet 외

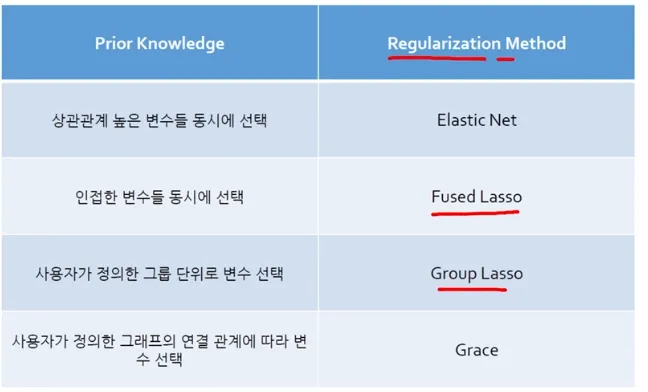
챕터02. Classification Problem

- Loss Function 설명

• Regression Loss Function Remind

  Regression Loss Function은 Error의 크기를 측정할 수 있었음
  하지만 Classification Loss Function은 옳고 그름 2가지 밖에 없음

  단 Class가 2개 이상일 수 있음

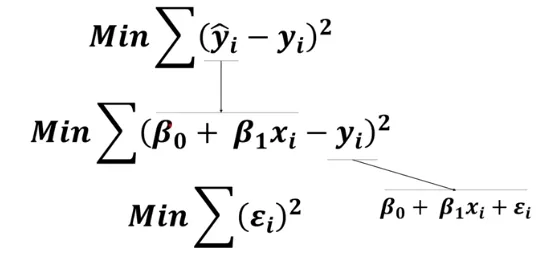
• Decision Tree

  가장 기본적인 Classification Model
  Decision Tree는 Regression Problem도 함께 적용 가능함

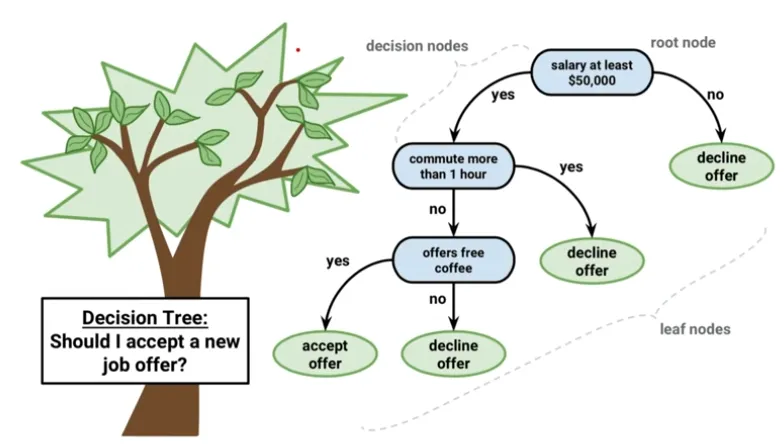
• Classification Measuring Impurity for Split

  순도(Homogeneity)를 최대로 증가시키는 방향
  불순도(Impurity) 혹은 불확실성(Uncertainty)을 최소로 감소시키는 방향

  Measuring Impurity 1 : Gini Index (Max 0.5, 0일 때 가장 잘 나누어진 것)

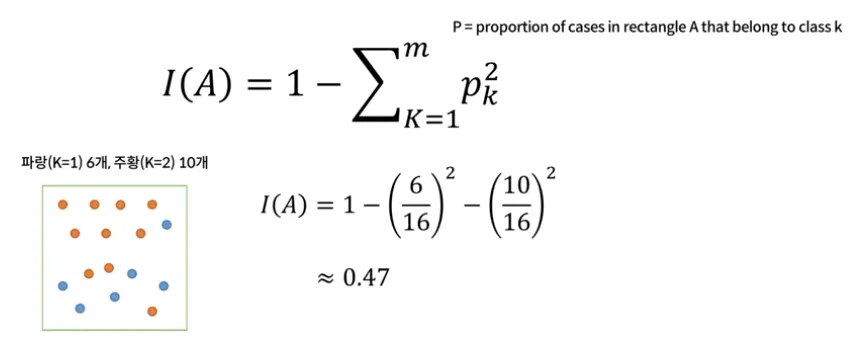
• Measuring Impurity 2 : Entropy (0일 때 가장 잘 나누어진 것)

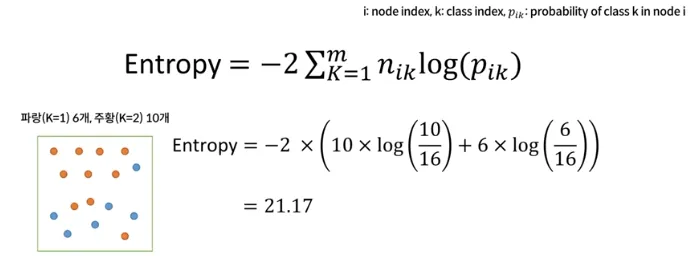
• Measuring Impurity 3 : Misclassification Error (잘 사용하지 않음)

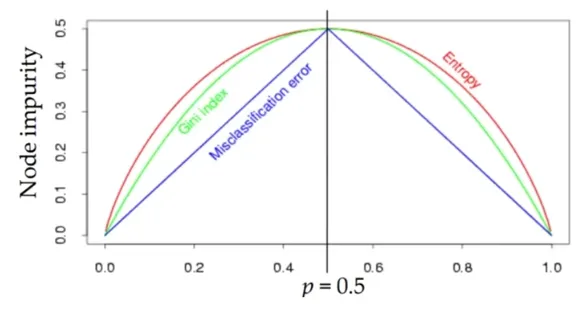
• Classification Loss Function

  기본적으로 Classification Model을 학습할 때 사용하는 Binary Cross Entropy

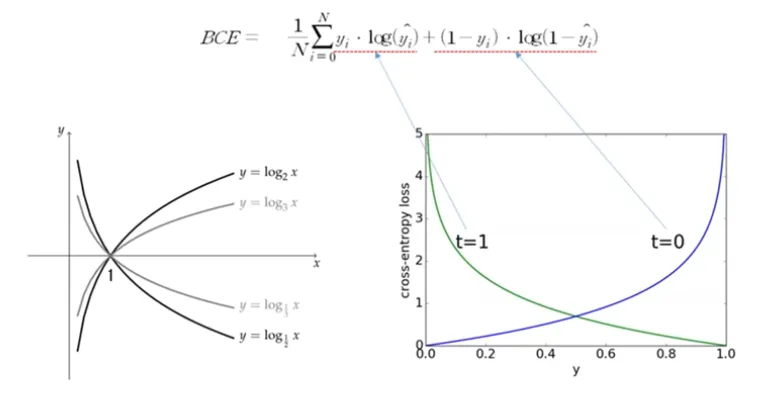
- Decision Tree 원리

• Decision Tree 기본적인 원리

  데이터를 분석하여 이들 사이에 존재하는 패턴을 예측 가능한 규칙(Rules)들의 조합으로 나타냄
  모양이 ‘나무’와 같다고해서 의사결정나무라고 불림
  질문을 던져서 대상을 좁혀 나가는 ‘스무고개’ 놀이와 비슷한 개념

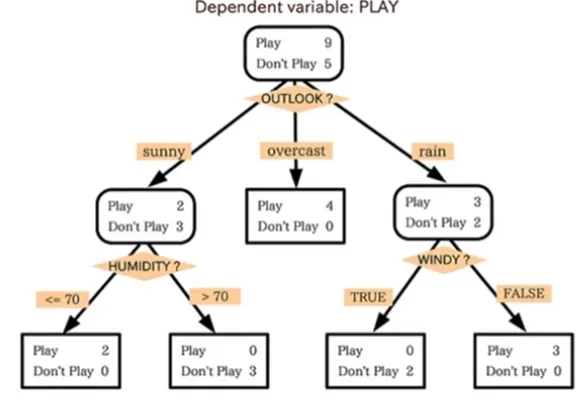
• Decision Tree 기본적인 원리 (2)

  Linear Regression과 다르게 Model의 Complexity를 극한으로 높일 수 있음( Overfitting이 일어날 수 있음)
  아래 예제와 같이 만약 Terminal node 수가 3개 뿐이라면 새로운 데이터가 100개, 1000개가 주어진다고 해도 의사결정나무는 정확히 3종류의 답(Rule)만을 출력하게 됨

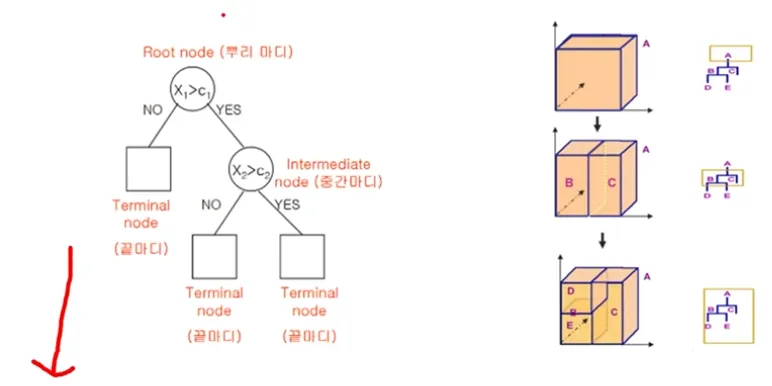
• Split을 통해 순도를 최대한 증가시키고 불순도를 낮춰야한다

  Gini Index 예시

• Decision Tree Split하는 원리

  First Step은 불순도가 가장 낮은 Feature와 포인트를 찾음

  이 포인트가 Root Node가 되는 것
  그 후 Information Gain이 가장 큰 포인트를 찾아서 Split을 진행함
  각 x의 scale은 독립적이다 (각 변수의 스케일이 달라도 되며 서로 영향x, 스케일링 필요x) 즉, 병렬적이라 엄청 빠르다

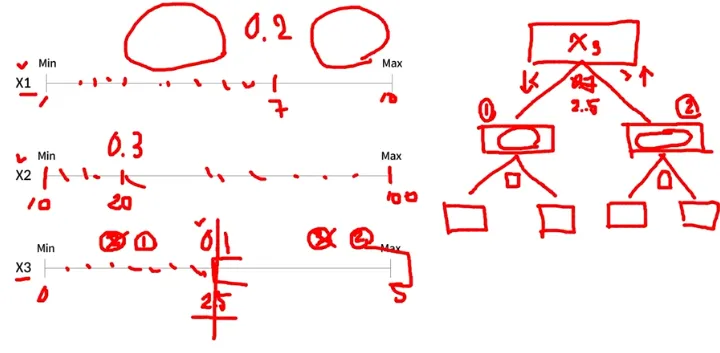
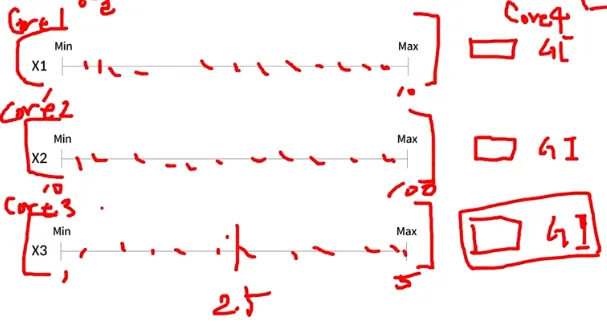
• Decision Tree 100% Purity, 0% impurity

  무한히 Partitioning (Split)을 하게 되면 100% Purity, 0% Impurity가 됨
  Overfitting 발생

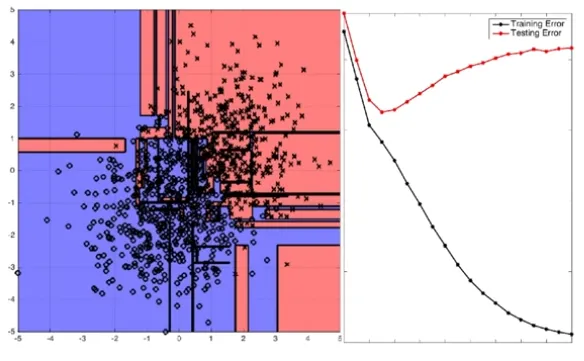
• Decision Tree Pruning

  모든 Terminal node의 불순도가 0, 순도가 100%인 상태를 Full Tree라고 정의함
  Full tree를 생성한 뒤 적절한 수준에서 Terminal node를 잘라줘야함

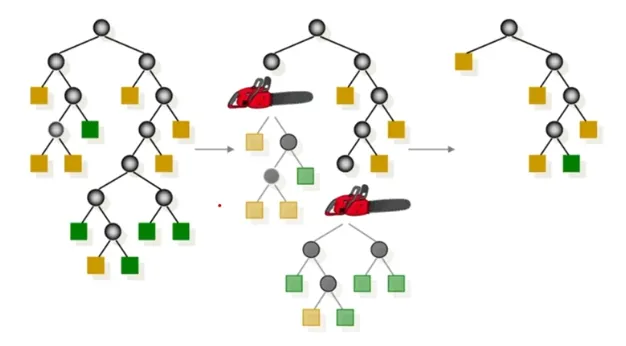
• Decision Tree

  Rule Extraction : 가장 중요하고 강력한 해석력을 가짐
  Simple 하지만 직관력이 있음 : Simple is the Best
  Model이 복잡해질수록 해석력은 현저히 떨어지게 됨

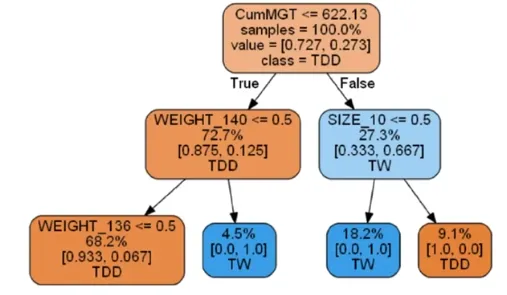
- Model 평가 및 지표 해석

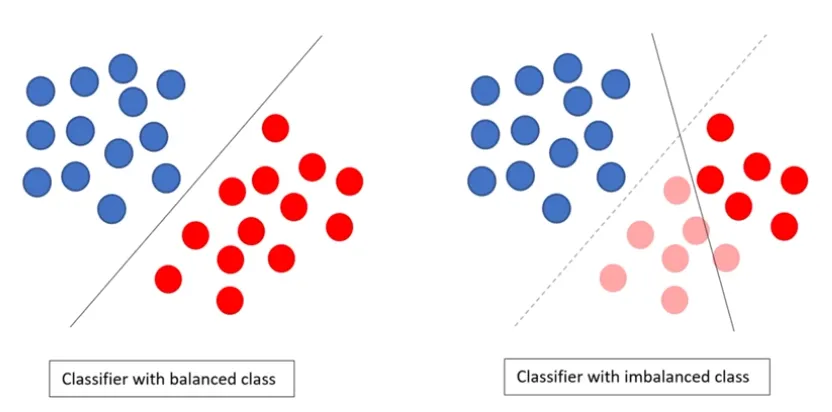
• Classification Model 평가 및 지표 해석 (1)

  고려사항 : Class의 Balance가 맞는가?
  → 평가 지표가 달라지게 됨

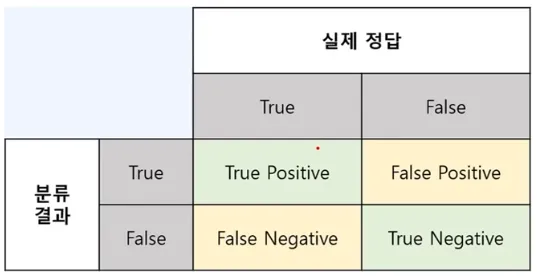
• Classification Model 평가 및 지표 해석 (2) - Confusion Matrix

  TP(True Positive), 참양성 : 예측한 값이 Positive이고 실제값도 Positive인 경우

  FN(False Negative), 거짓음성 : 예측한 값이 Negative이고 실제값은 Positive인 경우

  FP(False Positive), 거짓양성 : 예측한 값이 Positive이고 실제값은 Negative값인 경우

  TN (True Negative), 참음성 : 예측한 값이 Negative이고 실제값도 Negative인 경우

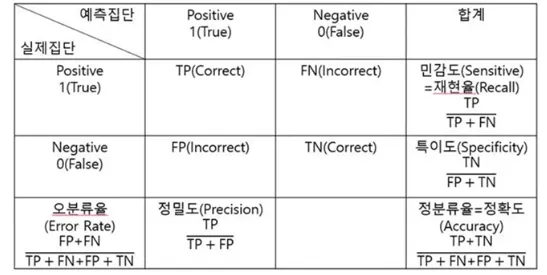
• Classification Model 평가 및 지표 해석 (3)

  정분류율(Accuracy) : 정확도는 직관적으로 모델 예측 성능을 나타내는 지표

  정밀도(Precision) : 예측 Positive 중 실제도 Positive를 찾아낸 비율
  (미처 잡아내지 못한 개수가 많더라도 더 정확한 예측이 필요한 경우)

  재현율(Recall) : 실제 Positive 중 올바르게 Positive를 예측해 낸 비율
  (잘못 걸러내는 비율이 높더라도 참값을 놓치는 일이 없도록 하는 것. 주예제 : 의학, 불량)

  특이도(Specificity) : 실제 Negative 중 올바르게 Negative를 찾아낸 비율

  Classification Model 평가 시 confusion matrix와 F1 Score 보는 것이 좋음

- Ensemble 정의

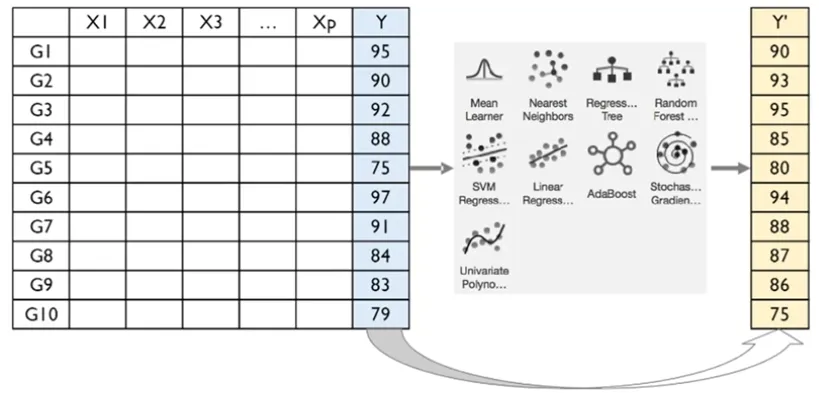
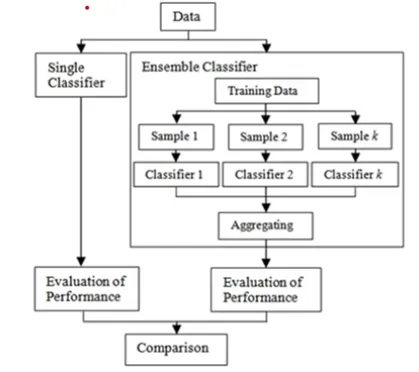
• Ensemble (앙상블)

  어떤 데이터를 학습할 때, 여러 개의 모델을 조화롭게 학습시켜 그 모델들의 예측 결과들을 이용하여 더 정확한 예측값을 구할 수 있음

• Ensembles almost always work better

  앙상블이 싱글모델보다 효과가 좋은 이유 수식 정리
  하지만 앙상블은 결과가 mix되어 있기 때문에 싱글모델보다 해석이 어렵다 (앙상블 대부분이 블랙박스 모델)
  블랙박스 모델을 파헤치는 과정 지속적 개발 중 : XAI(Explainable Artificial Intelligence), Interpretable 머신러닝

  앙상블 모델은 모델의 복잡성 올라가지만 (정확도는 높아지지만) 모델의 해상력이 떨어진다 → 도메인이나 데이터의 특성(복잡도)에 맞는 적절한 알고리즘을 사용해야 한다

• 2014년 179개 알고리즘 121개 Data Set에 적용한 실험 결과

  Random Forests (의사결정나무의 앙상블)과 SVM 계열이 상대적으로 분류 성능이 높게 나타남

• MLConf SF(샌프란시스코 머신러닝 컨퍼런스, 2016) - TOP10 main takeaways

  딥러닝이 전부가 아니다 (It’s (still) not all about Deep Learning)

  상황에 맞는 평가지표를 활용해라 (Choose the right problem to solve, with the right metric)

  Model tuning하는데 있어 시간을 많이 투자하지 마라 (Fine tuning your models in 5% of a project)

  Ensembles almost always work better

  개인화 혹은 초개인화가 트렌드 (The trend towards personalization)

  널리 알려진 컨텐츠들은 아직도 잘 먹힌다 (Manual curation of content is still used in practice)

  차원의 저주를 피해라, overfitting (Avoid the curse of complexity)

  잘 알려진 혹은 유명한 BP 사례를 배워라 (Learn the best practices from established players)

  오픈 소스를 잘 활용해라 (Everybody is using open source)

  프로젝트를 진행하기 전 경영진의 지원이 있는지 확인해라 (Make sure you have support from the executives)

• 앙상블은 항상 모델의 성능을 향상시킬까?

  어떤 알고리즘도 모든 상황에서 다른 알고리즘보다 우월하다는 결론을 내릴 순 없음
  문제의 목적, 데이터 형태 등을 종합적으로 고려하여 최적의 알고리즘을 선택할 필요가 있음

- Ensemble 종류 (Bagging, Boosting, Stacking)

• Ensemble 종류

  Bagging : Reduce the variance

  Stacking : Use another prediction model

  Boosting : Reduce the bias

• Bagging

  여러 데이터셋으로 샘플링 한 후 같은 알고리즘으로 여러 결론을 도출해 가장 많은 결론 도출

  Bootstrap Aggregating

  Bootstrap : 표본에서 추가적으로 표본을 복원추출하고 각 표본에 대한 통계량을 다시 계산하는 것
  N개의 Data가 있으면 N개를 Randomly하게 뽑아내서 새로운 Data Set을 구성함
  Bootstrap을 진행하면 확률상 뽑히지 못한 데이터는 36.8%가 됨

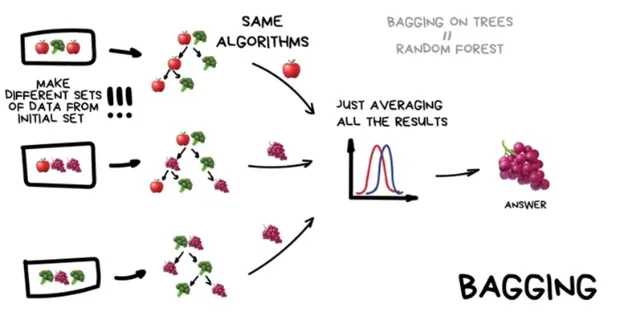
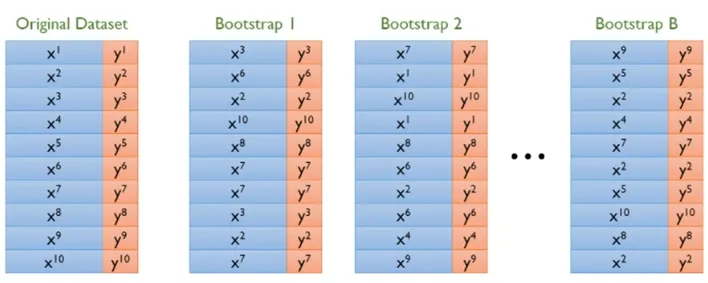
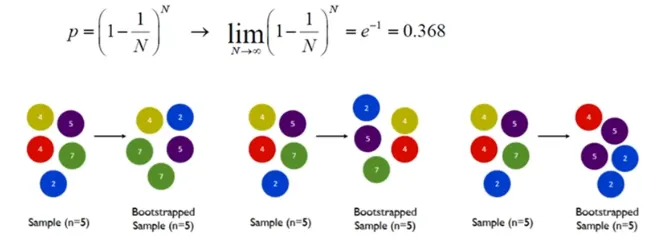
• Bagging Model Result Aggregating Method 1 : Majority voting

• Bagging Model Result Aggregating Method 2 : Weighted voting 1

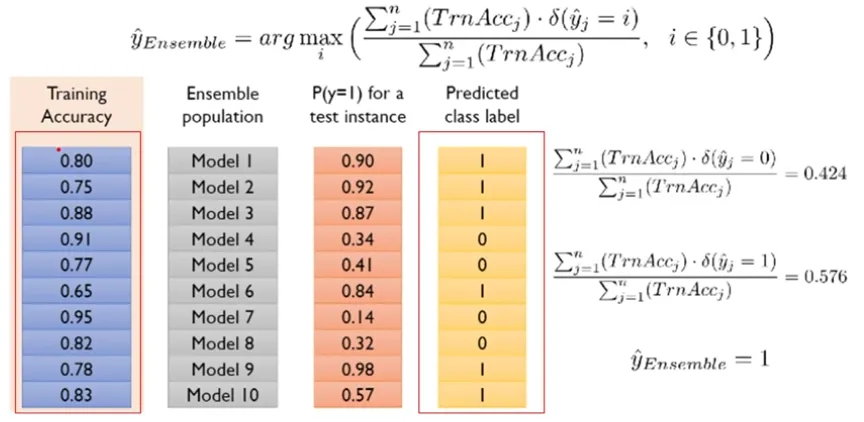
• Bagging Model Result Aggregating Method 2 : Weighted voting 2

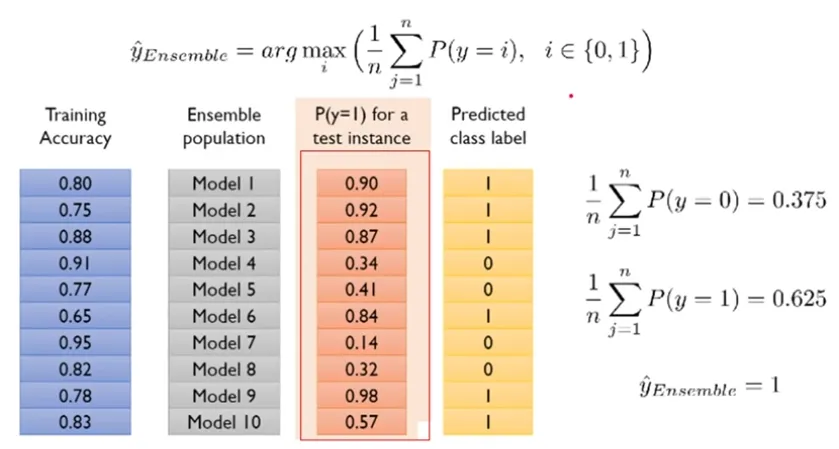
• Bagging Model Result Aggregating Method의 다양한 Rule

  도메인에 맞게 활용

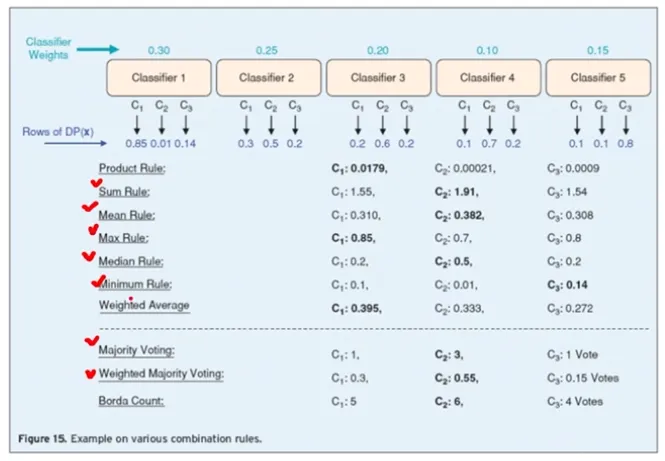
• Stacking

  같은 샘플 데이터 셋, 다른 알고리즘 모델

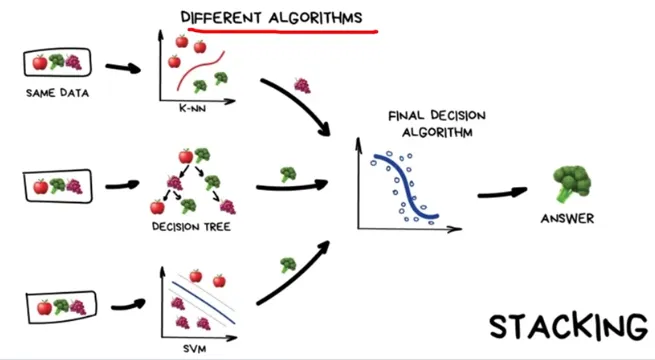
• Boosting

  처음 알고리즘 모델을 통해 맞추지 못한 데이터에 대해 학습 확률을 높여 새로운 데이터 셋을 만든다(우선순위 배정) → 맞출 때 까지 반복
  노이즈까지 학습해버릴 수 있으니 데이터 전처리 매우 중요

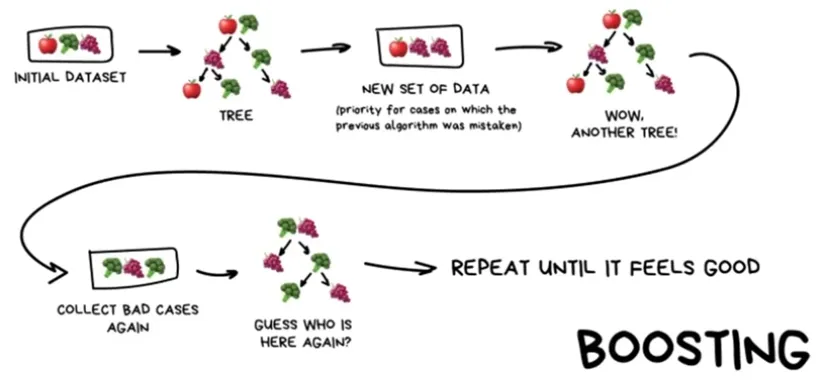
- Random Forest 설명 & 실습

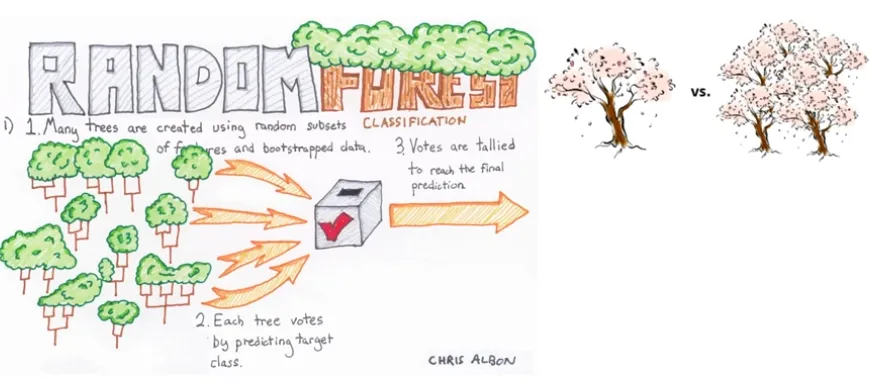
• Random Forest (1)

  Raodom decision forests (1995) - Bell Labs의 Tin Kam Ho 박사
  (단순 여러 개의 Decision Tree를 랜덤하게 고른 Feature로 학습한 후 조합)

  Random Forests (2001) - UC Berkeley 통계학과 Leo Breiman 교수
  (Random Decision Forests + Bagging 기법 추가)

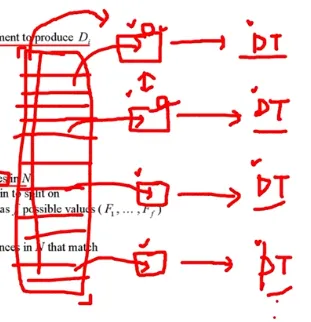
• Random Forest (2)

  A specialized bagging for decision tree algorithm
  Two ways to increase the diversity of ensemble

  else 는 행뿐 아니라 열로서도 나누는 것이므로 데이터 셋별로 상관성이 매우 낮아지게 되는 것 → 다양성 증가

• Random Forest - Two ways to increase the diversity of ensemble

  Bagging
  Randomly chosen predictor variables (x들)

  Tree는 작은 Bias와 큰 Variance를 갖기 떄문에, 매우 깊이 성장한(Depth가 깊은) 트리는 훈련 데이터에 의해 Overfitting하게 됨

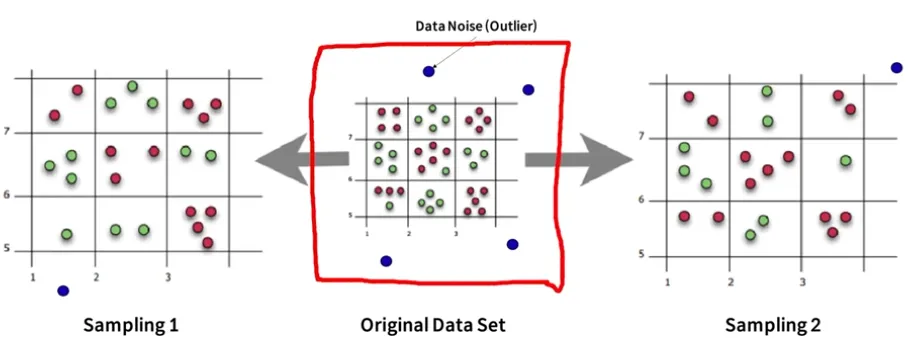
  한 개의 Tree의 경우 훈련 데이터에 있는 Noise에 대해 매우 민감함

  Tree들이 서로 상관화(correlated)되어 있지 않다면 여러 Tree들의 평균은 Noise에 대해 강인해짐
  상관화를 줄이는 방법은 Randomly Chosen (행 & 열 모두)
  반면, Forest를 구성하는 모든 Tree들을 동일한 데이터 셋으로만 훈련시키게 되면, Tree들의 상관성은 커짐

  따라서 Bagging은 서로 다른 데이터 셋들에 대해 훈련시킴으로서, Tree들을 비상관화 시켜주면 됨

  Bias는 유지하면서 Variance를 낮춤

  복잡한 noise한 데이터도 학습하지 않기 떄문에 variance가 낮아지는 거

• Random Forest - Out Of Bag (OOB)

  Bootstrap을 진행하면서 확률 상 뽑히지 못한 데이터는 36.8%가 됨
  뽑히지 못한 Data를 활용하여 Model의 성능을 측정함
  대게 Model의 성능을 측정할 때, Train set과 Valid set을 나눔
  하지만 Random forest의 경우 Valid set을 나눌 필요가 없음
  → 뽑히지 못한 36.8% OOB Data를 활용!

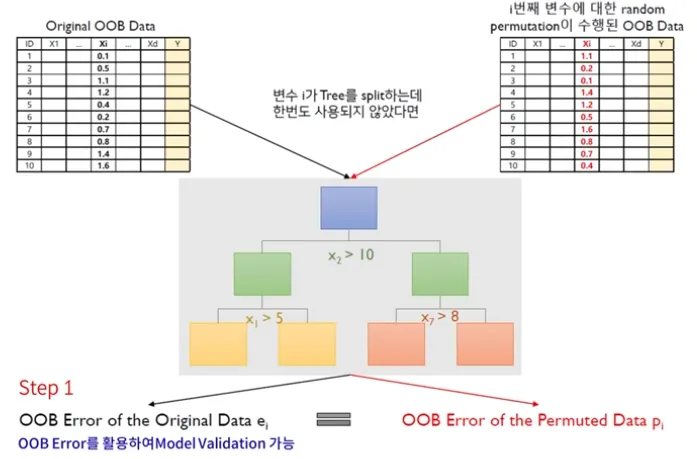
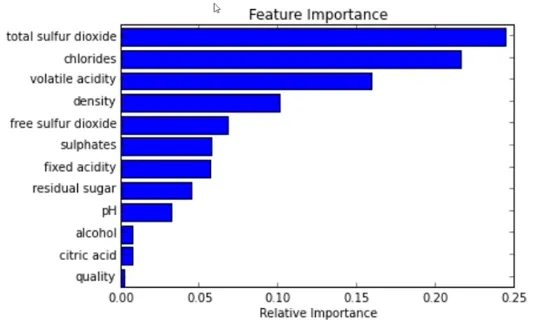
• Random Forest - Out Of Bag 활용 Feature Importance Score

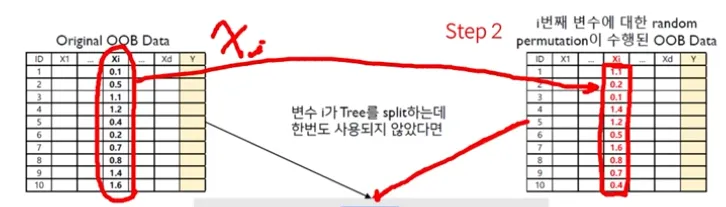
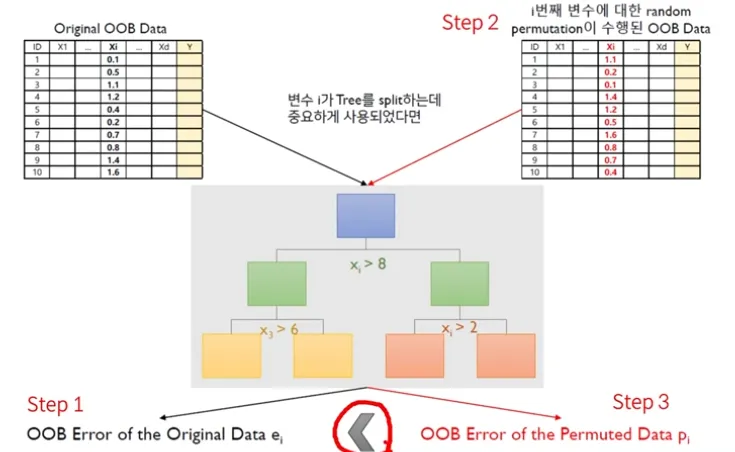
  Step 1 : Compute the OOB error for the original dataset

  Step 2 : Compute the OOB error for the dataset in which the variable x_i is permuted p_i

  Step 3 : Compute the variable importance based on the mean and standard devision of over all trees in the population

  만약 작거나 같으면 OOB Error of the permuted data는 중요하지 않은 데이터가 된다

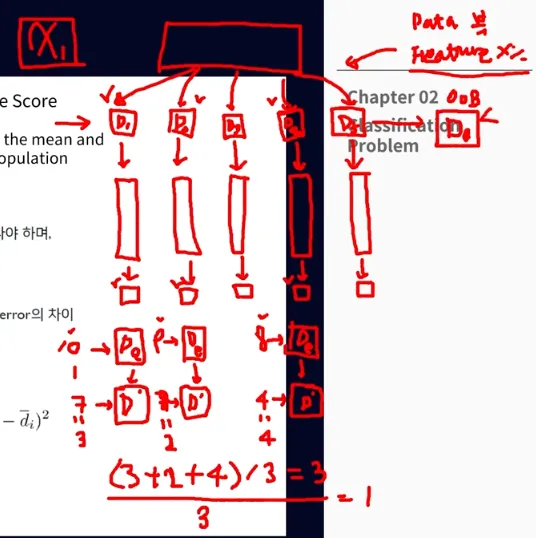
• 랜덤 포레스트에서 변수의 중요도가 높다면

  1) Random permutation 전-후의 OOB Error 차이가 크게 나타나야 하며

  2) 그 차이의 편차가 적어야 함

  큰 인사이트를 얻진 못한다

  가장 큰 영향력을 주는 건 알겠는데 어떻게 주는데?
  드릴다운 분석을 계속 하며 밀접 관계를 파악해야 함 (비선형적이라 상관관계를 파악하긴 어렵지만) → 분석의 해석력을 높여야 한다

• 요즘엔 배깅 연구는 조금 더디고 Boosting이 활발한 상황

  Ada boost → GBM - > XG Boost → Light GBM → Cat Boost → N Boost 등

    "이 글은 제로베이스 데이터 분석 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다."