DFS & BFS
그래프
1. 그래프 용어
1. 그래프(Graph)
- 현실 세계의 사물이나 추상적인 개념간의 연결관계를 표현
- 일반적이고 강력한 자료구조
- ex) 섬들을 연결하는 다리만들기
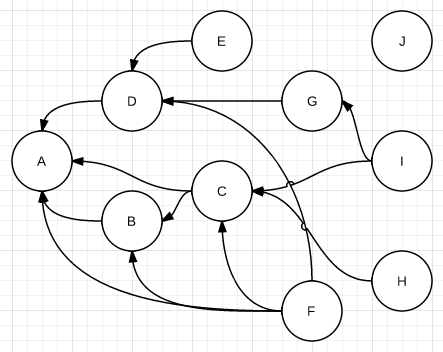
- 정점과 간선으로 구성
- 정점: Node, Vertex
- 간선: Edge ⇒ 정점간의 관계 표현
2. 경로(Path)
- 끝과 끝이 서로 연결된 간선들을 순서대로 나열한 것
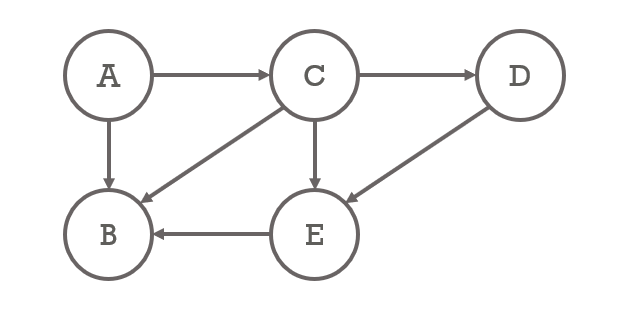
- A → E로 가는 경로
- A → C → D → E
- A → C → E
- 단순 경로: 경로 중 한 정점을 두 번 이상 방문하지 않는 경로
3. 사이클(Cycle)
- 시작한 점에서 끝나는 경로
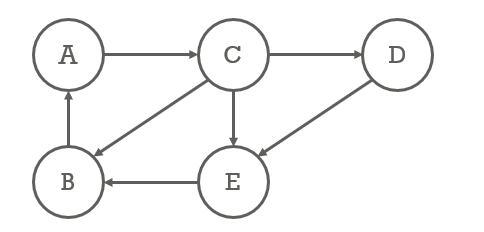
- 사이클
- A → C → B → A
- C → D → E → B → A → C
- ETC…
- 단순 사이클: 한 정점을 두 번 이상 방문하지 않는 사이클(시작점 제외)
4. 방향 그래프(Directed Graph)
- 간선에 방향성이 있는 그래프
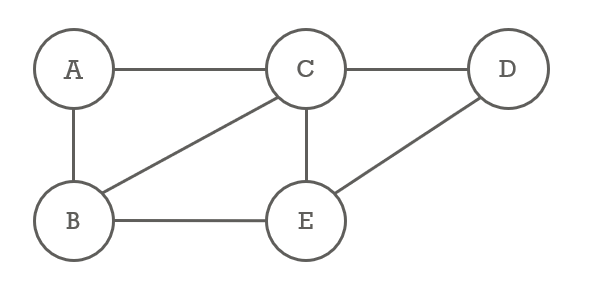
5. 무방향 그래프(Undirected Graph)
- 간선에 방향이 없는 그래프 = 양방향 그래프
6. 루프(Loop)
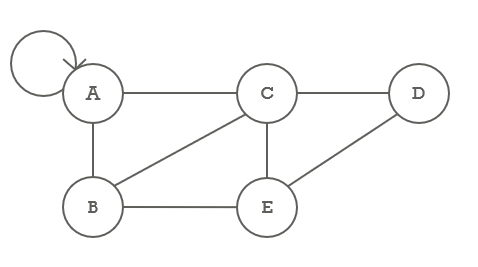
- A → A와 같이 사이클을 이루는 것
7. 가중치(Weight)

- 간선에 주어진 값
- A → C로의 시간, 비용, 거리 등등
- 가중치가 없는 경우 1이라고 생각하고 문제 풀이
8. 차수(Degree)
- 한 정점에 연결되어 있는 간선의 개수
- 방향 그래프의 경우에는
indegree와outdegree로 구분된다
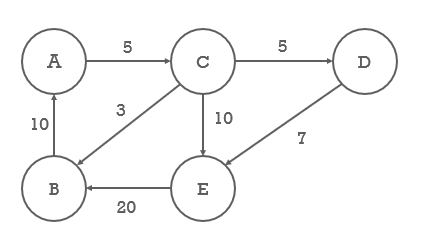
- C의 차수
- degree = 4
- indegree = 1
- outdegree = 3
9. 연결 성분(Connected Component)
- 연결된 덩어리

10. 인접 행렬(Adjacency Metrix)
- 정점의 개수가 n개일 때, 그래프의 연결관계를 n*n의 이차원 배열로 나타낸 것
- 공간 복잡도 O(N^2)
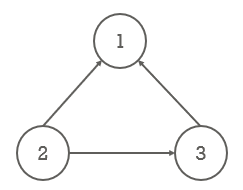
⇒

- 장점
- 구현이 쉽다
- 노드 i와 j의 연결 여부를 알고 싶을 때, adj[i][j]가 1인지 0인지 확인하면 되기에
O(1)즉, 상수의 시간 복잡도를 갖는다
- 단점
- i번 노드와 연결된 모든 노드를 방문하고 싶을 때, adj[i][1]부터 adj[i][n] 모두 확인해야 하기에
O(N)의 시간 복잡도를 갖는다 → N개의 노드 모두 연결된 노드를 방문할 때는O(N^2)의 시간복잡도 - 특히, 노드의 개수에 비해 간선의 개수가 적은 그래프일 경우에는 엄청나게 비효율적일 수 있다
- ex) 10000개의 노드에 간선의 개수가 1개
- i번 노드와 연결된 모든 노드를 방문하고 싶을 때, adj[i][1]부터 adj[i][n] 모두 확인해야 하기에
for(int i = 0; i < edge; i++)
{
int a, b;
a = sc.nextInt();
b = sc.nextInt();
adj[a][b] = 1;
//adj[b][a] = 1;
//무방향 그래프일 때는
//노드 a에서 노드 b로 가는 간선이 존재한다면
//노드 b에서 노드 a로 가는 간선도 존재한다고 생각할 수 있음
}11. 인접 리스트(Adjacency List)
- 리스트를 이용하여 구현
- 헤드 노드를 묶어 이차원 리스트로 구현
- 공간복잡도: O(V+E)
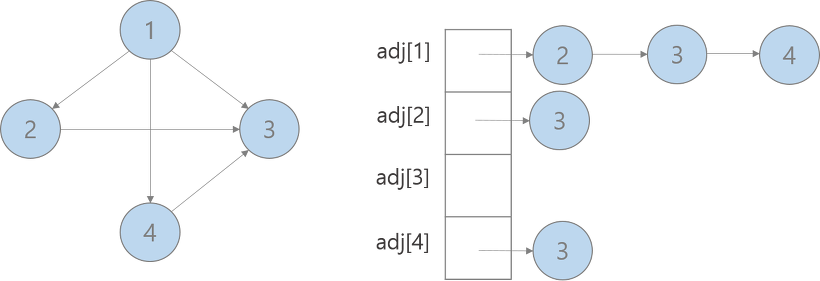
cf) 리스트에서 adj[1]에 있는 3개의 노드의 순서는 의미 X 4, 3, 2 순서여도 무관하다. 하지만 보기 좋게 오름차순으로 정렬한 것
- 장점
- 인접 행렬과 달리 실제로 연결된 정보만 저장하기 때문에 간선의 개수에 비례하는 공간복잡도
- 인접 행렬의 경우 2번 노드에서 연결된 노드를 방문하고 싶다면 adj[2][1]부터 adj[2][4]까지 방문해야 하지만 인접 리스트의 경우 adj[2]의 size만큼만 확인하면 된다
- 즉, 모든 노드에서 연결된 모든 노드를 방문하는 경우의 시간복잡도 = O(E)
- 단점
- 노드 i와 노드j가 연결되고 싶은지 확인해야 할 경우 인접행렬과 달리 adj[i][0] ~ adj[i]adj[i].size()-1] 까지 방문해야 하므로 O(V)의 시간 복잡도를 갖는다
ArrayList<ArrayList<Integer>> adj = new ArrayList<ArrayList<Integer>>();
for(int i=0;i<=n;i++) {
adj.add(new ArrayList<Integer>());
}
for(int i=0;i<m;i++) {
int a = sc.nextInt();
int b = sc.nextInt();
adj.get(v1).add(v2);
adj.get(v2).add(v1); //무방향 그래프의 경우
}2. 그래프 탐색 알고리즘
- DFS(Depth First Search):
Stack이용 - BFS(Breadth First Search):
Queue이용
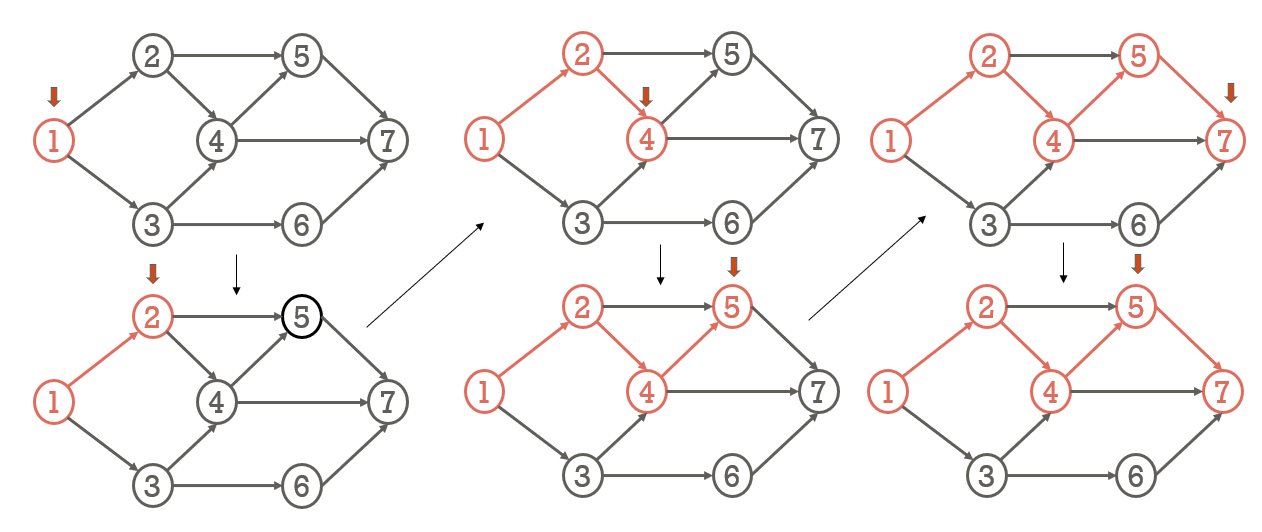
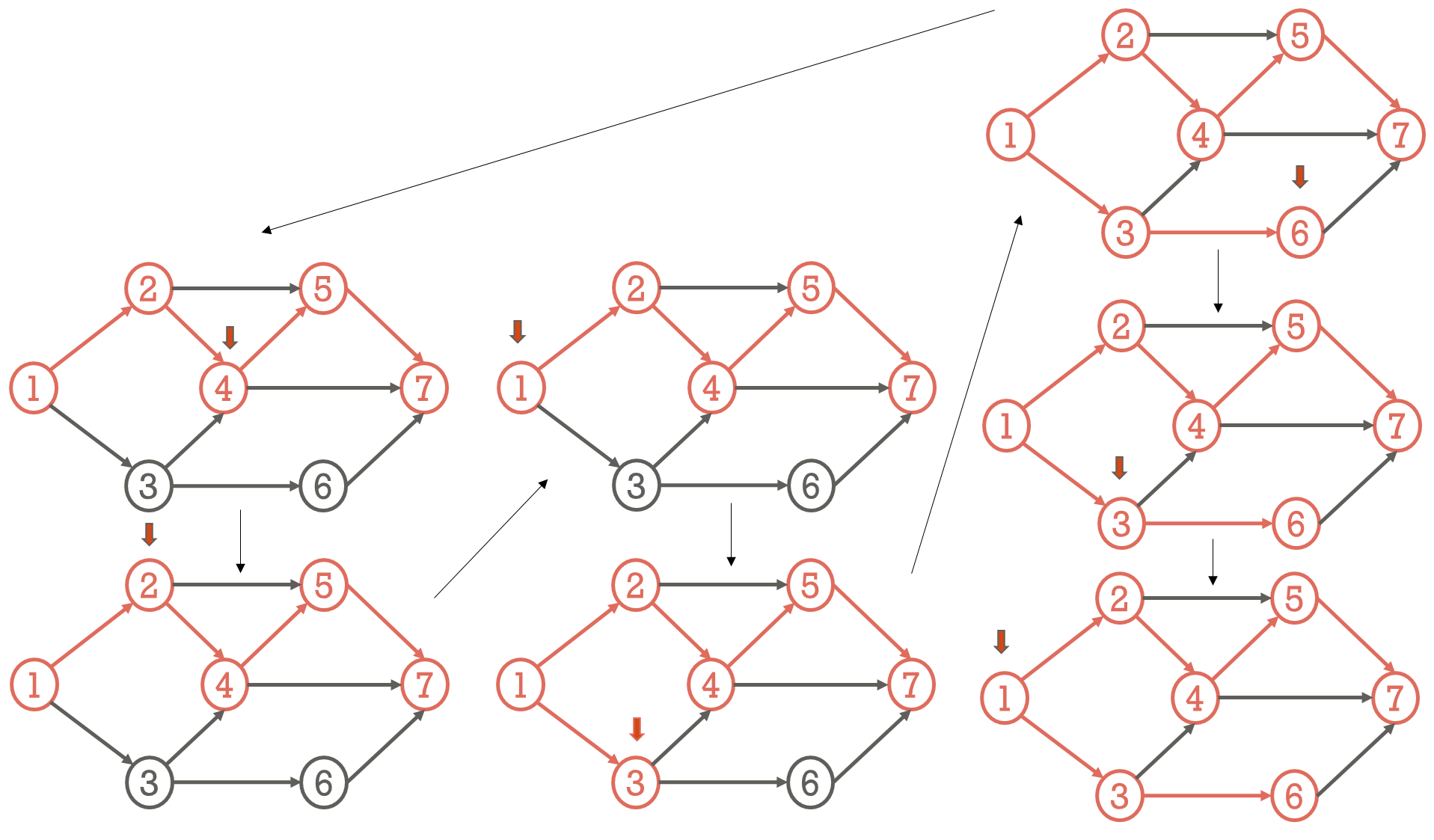
(1) DFS
- 동작 방식 (정점 v 시작)
- v 방문
- v에 인접한 정점들 중 아직 방문하지 않은 정점 w 방문
- w에 인접한 정점들 중 아직 방문하지 않은 정점 x 방문
- 재귀적으로 모든 정점을 방문할 때 까지 DFS 수행
void dfs(ArrayList<ArrayList<Integer>> adj, boolean[] check, int now) {
if(check[now] == true) return; // 재귀호출 종료 부, 방문한 적이 있으면 메소드 종료
check[now] = true; // 방문한 적 없는 정점이라면 방문 처리
System.out.println(now+"번 노드 방문"); // 방문한 정점 출력
// 바깥쪽 ArrayList의 인덱스인 정점과 연결된 정점을 탐색
for(int i = 0; i < adj.get(now).size(); i++) {
int next = adj.get(now).get(i);
if(!check[next]) // 연결된 정점이 방문한 적 없다면
dfs(adj, check, next); // 재귀호출로 깊이 우선 탐색 실행
}
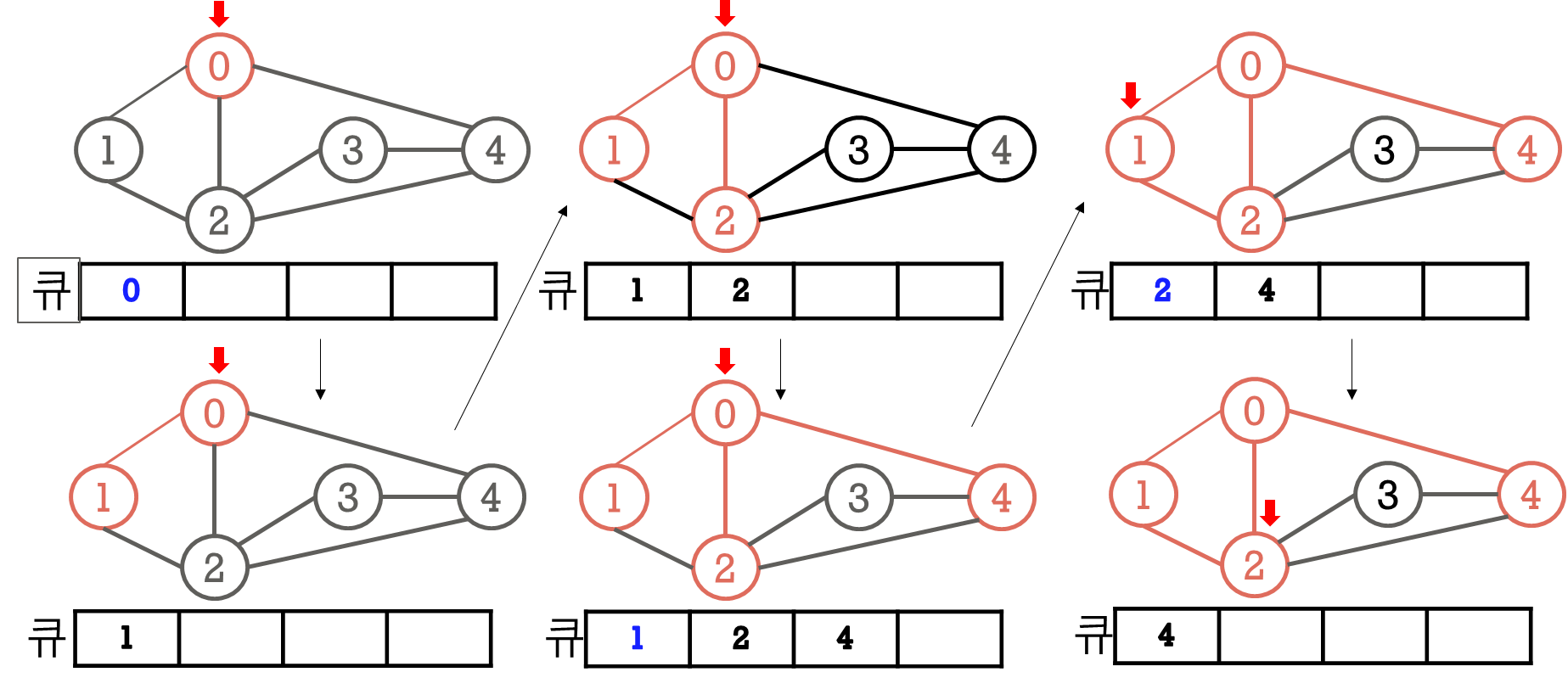
}(2) BFS
- 동작 방식 (정점 v 시작)
- v 방문
- v에 인접한 정점 차례로 방문
- 2번에서 방문한 순서대로 각 정점에서 인접한 정점 방문
- 위 과정을 모든 정점을 방문할 때 까지 반복
- 적합한 자료구조:
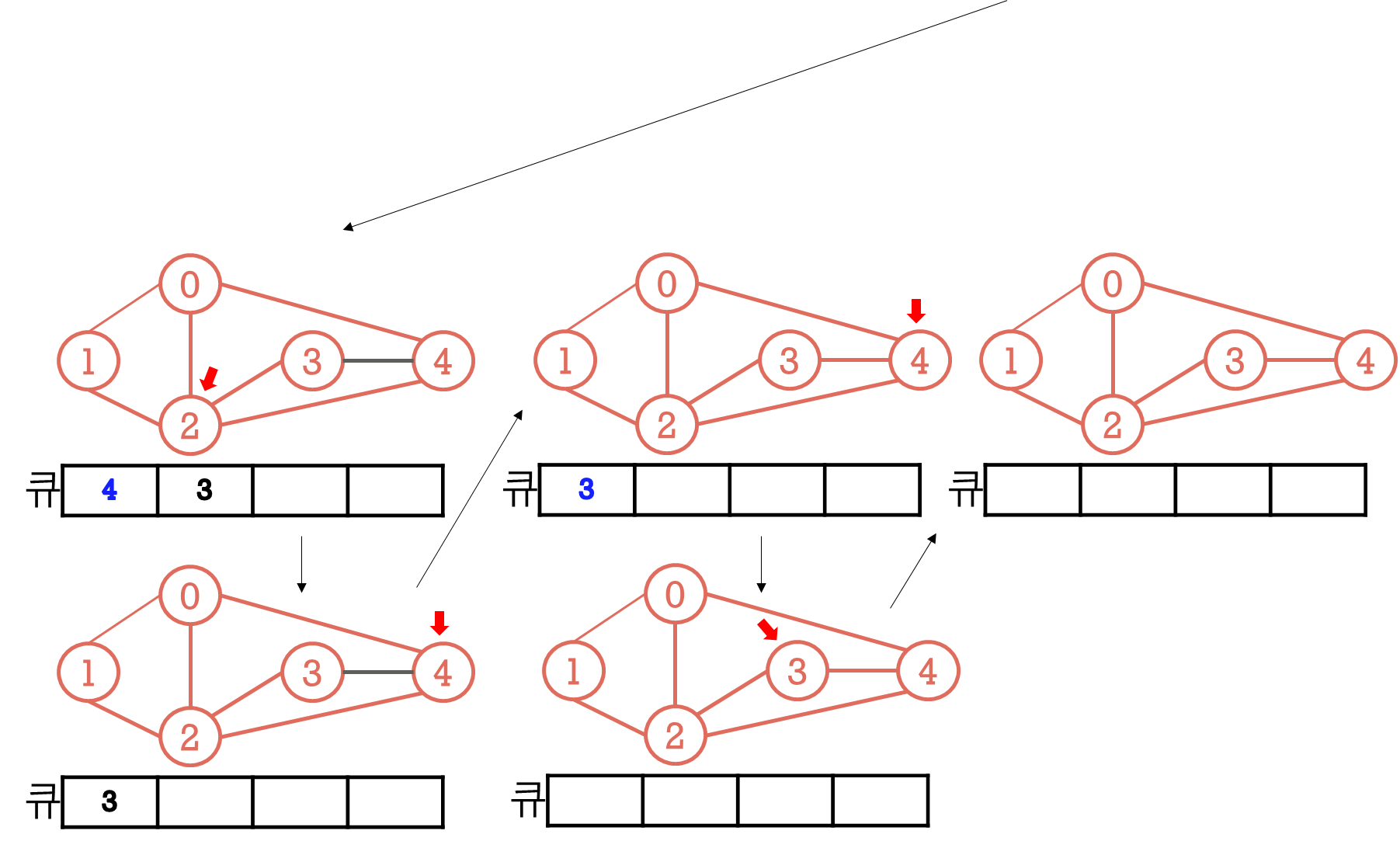
Queue- 방문한 정점의 인접한 정점들을 Queue에 push
- 다음으로 방문 할 정점을 Queue에서 pop하여 얻음
void bfs(ArrayList<ArrayList<Integer>> adj, boolean[] check, int start) {
Queue<Integer> q = new LinkedList<>(); // BFS를 위한 큐 객체
q.add(start); // 시작 정점을 큐에 삽입
check[start] = true; // 방문처리를 한다.
while(!q.isEmpty()) { // 큐가 빌 때 까지 반복
int now = q.poll(); // 큐에 삽입되어 있는 정점을 하나 가져온다.
System.out.println(now+"번 노드 방문"); // 해당 정점을 출력
// 바깥쪽 ArrayList의 인덱스인 정점과 연결된 정점을 탐색해 모두 큐에 삽입
for(int i = 0; i < adj.get(now).size(); i++) {
int next = adj.get(now).get(i);
if(!check[next]) { // 방문하지 않았던 정점이라면
q.add(next);
check[next] = true; // 해당 정점을 방문 처리한다.
}
}
}
}3. 예제
- Code
import java.util.*; class Main { static void dfs(ArrayList<ArrayList<Integer>> adj, boolean[] check, int now) { if(check[now] == true) return; check[now] = true; System.out.print(now+" "); for(int i = 0;i<adj.get(now).size();i++) { int next = adj.get(now).get(i); if(!check[next]) dfs(adj, check, next); } } static void bfs(ArrayList<ArrayList<Integer>> adj, boolean[] check, int start) { Queue<Integer> q = new LinkedList<>(); q.add(start); check[start] = true; while(!q.isEmpty()) { int now = q.poll(); System.out.print(now+" "); for(int i = 0;i<adj.get(now).size();i++) { int next = adj.get(now).get(i); if(!check[next]) { q.add(next); check[next] = true; } } } } public static void main(String[] args) { Scanner sc = new Scanner(System.in); int n = sc.nextInt(); int m = sc.nextInt(); int start = sc.nextInt(); ArrayList<ArrayList<Integer>> adj = new ArrayList<ArrayList<Integer>>(); boolean check[] = new boolean[n+1]; for(int i=0;i<=n;i++) { adj.add(new ArrayList<Integer>()); } for(int i=0;i<m;i++) { int v1 = sc.nextInt(); int v2 = sc.nextInt(); adj.get(v1).add(v2); adj.get(v2).add(v1); } for(int i=1;i<=n;i++) { Collections.sort(adj.get(i)); } dfs(adj,check,start); Arrays.fill(check, false); System.out.println(); bfs(adj,check,start); } }
행렬 문제 접근법
static int[] dx = {0, -1, 0, 1};//우 상 하 좌
static int[] dy = {1, 0, -1, 0};
static void bfs(int x, int y) {
Queue<int[]> q = new LinkedList<int[]>();
q.add(new int[]{x, y});
while (!q.isEmpty()) {
x = q.peek()[0];
y = q.peek()[1];
visit[x][y] = true;
q.poll();
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (0 <= nx && nx < M && 0 <= ny && ny < N) {
if (!visit[nx][ny] && map[nx][ny] == 1) {
q.add(new int[]{nx, ny});
visit[nx][ny] = true;
}
}
}
}
}