Merge Sort(병합정렬)

Merge Sort도 quick Sort처럼 분할 정복 알고리즘에 해당하는 알고리즘입니다. Merge Sort는 정확히 반으로 나누어서 서로 비교하여 하나로 합쳐가는 정렬 방식입니다.

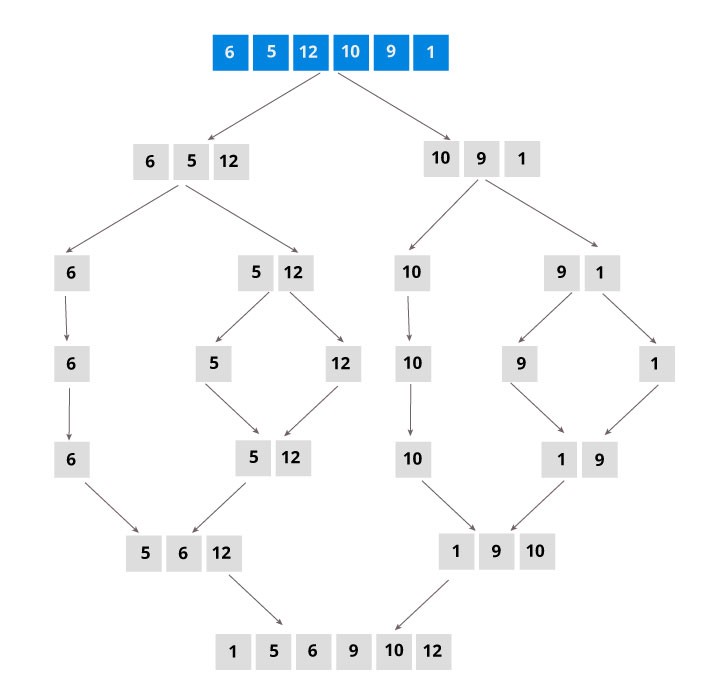
Quick Sort는 pivot 값으로 인하여 최악의 경우 O(N^2)의 알고리즘 성능이 나올 수 있지만 Merge Sort는 O(N*logN)을 보장합니다.

Merge Sort Code

#include<iostream>

int number = 9;
int sorted[9];
int size;
int count = 0;

void merge(int a[], int m, int middle, int n)
{
	int i = m;
	int j = middle + 1;
	int k = m;
	
	while(i <= middle && j <= n)
	{
		if(a[i] <= a[j])
		{
			sorted[k] = a[i];
			i++;
		} else {
			sorted[k] = a[j];
			j++;
		}
		k++;
	}
	
	if(i > middle) {
		for(int t = j; t<= n; t++)
		{
			sorted[k] = a[t];
			k++;
		}
	} else {
		for(int t= i ; t <= middle ; t++)
		{
			sorted[k] = a[t];
			k++;
		}
	}
	
	for(int t = m ; t <= n ; t++)
	{
		a[t] = sorted[t];
	}
}

void mergeSort(int a[], int m, int n)
{
	if(m < n) 
	{
		int middle = (m + n) / 2;
		mergeSort(a, m, middle);
		mergeSort(a, middle + 1, n);
		merge(a, m, middle, n);
	}
}

int main()
{
	int data[] = {5, 8, 2, 7, 4, 1, 9, 6, 3};
	mergeSort(data, 0, number - 1);
	
	
	for( int i = 0 ; i < 9 ; i++)
		std::cout<< data[i] << " ";
	
	return 0;

}

이미지 출처
자료 출처