그래프(Graph)

개념

노드(Node)와 그 노드를 연결하는 간선(Edge)을 하나로 모아놓은 자료구조. 즉, 연결되어 있는 객체 관계를 표현할 수 있는 자료구조 이다.

• 예: 지도, 지하철 노선도 등

특징

• 그래프는 네트워크 모델이다.
• 두 개 이상의 경로가 가능하다.(양방향 경로 가능)
• selp-loop 뿐 아니라 loop/circuit 모두 가능하다.
• 루트 노드의 개념이 없다.
• 부모-자식 개념이 없다.
• 순환 혹은 비순환이 존재한다.

종류

무방향 그래프

• 간선을 통해 양 방향으로 갈 수 있다.
• 정점 A와 B를 연결하는 간선은 (A, B) 혹은 (B, A) 로 표현한다.

방향 그래프

• 간선에 방향성이 존재한다.
• A에서 B로 가는 간선은 <A, B> 로 표현한다.(<A, B> 와 <B, A>는 다름)

가중치 그래프

• 간선에 가중치(비용 등)가 할당된 그래프

연결 그래프

• 무방향 그래프의 모든 정점쌍에 대해, 항상 경로가 존재

비연결 그래프

• 무방향 그래프에서 특정 정점쌍 사이에 경로가 존재하지 않음

완전 그래프

• 그래프에 속해 있는 모든 정점이 서로 연결되어 있는 그래프
• 정점의 수가 n일 경우, 간선의 수는 n*(n-1)/2

해시 테이블

개념

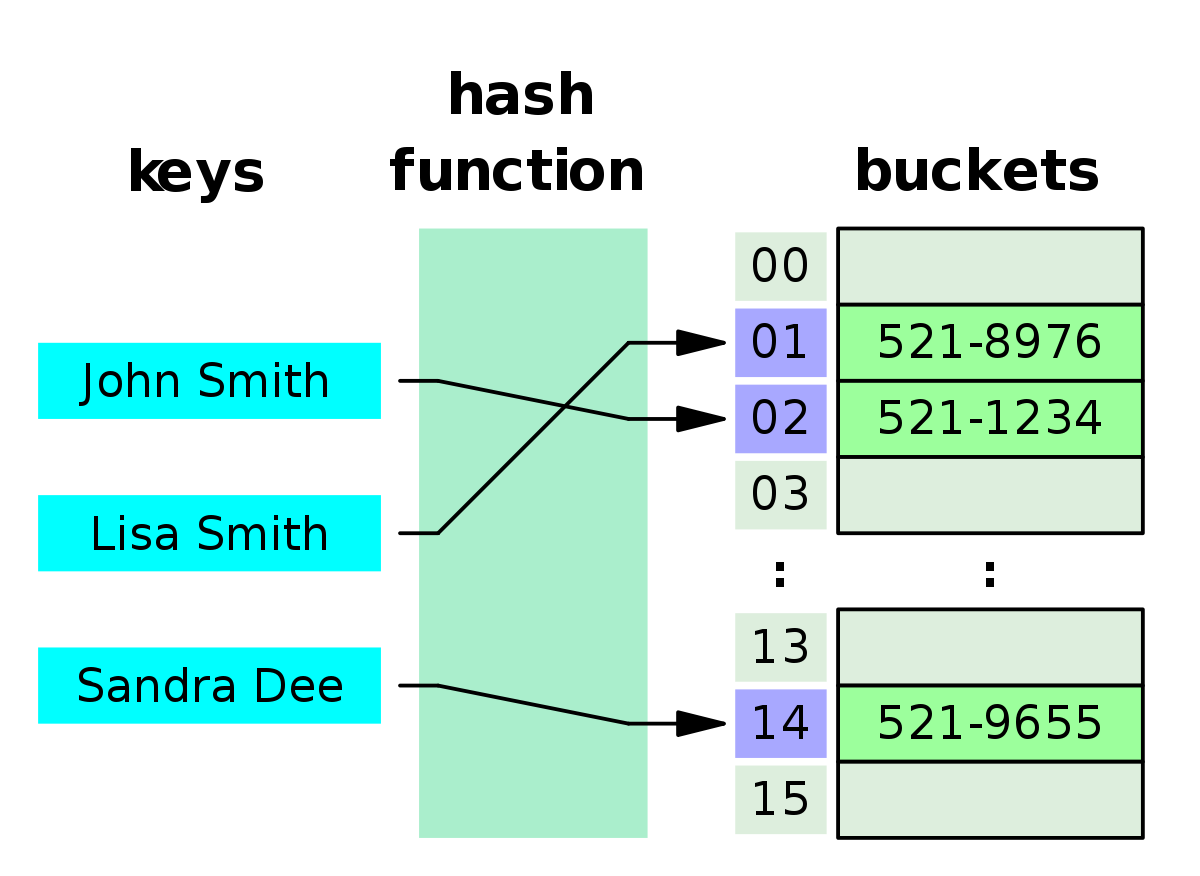
• 해시 테이블은 (Key, Value)로 데이터를 저장하는 자료구조 중 하나로, 빠른 데이터 검색이 가능하다.
• 해시 테이블의 검색이 빠른 이유는 버킷이라는 배열을 사용하여 데이터를 저장하기 때문이다.
• 해시 테이블은 각각의 key값에 해시함수를 적용해 배열의 고유한 index를 생성하고, 이index를 활용해 값을 저장하거나 검색하게 된다. 이 때, 실제 값이 저장되는 장소를 버킷 혹은 슬롯 이라고 한다.
  

충돌

• 해시 테이블에서 동일 인덱스에 두 개의 값이 충돌할 수 있다. 이를 해결하기 위해 해시 테이블은 분리 연결법과 개방 주소법을 사용한다.

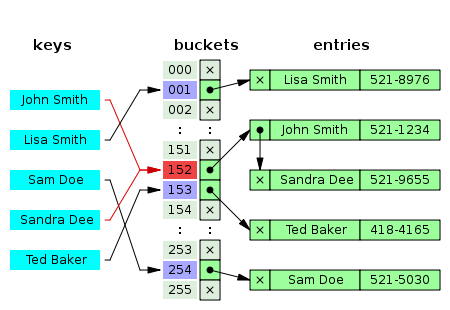
분리 연결법(Separate Chaining)

• 동일한 버킷의 데이터에 자료구조를 활용해 추가 메모리를 사용하여 다음 데이터의 주소를 저장한다.
• Chaining 방식은 해시 테이블의 확장이 필요없고 구현,삭제가 쉽다. 그러나, 데이터 수가 많아지면 동일 버킷에 chaining되는 데이터가 많아지며, 캐시의 효율성이 감소한다.
  

개방 주소법(Open Addressing)

• 비어있는 해시 테이블의 공간을 활용한다. 이를 구현하기 위해 다음 세 가지의 기법을 사용한다.
  1) Linear Probing : 현재 버킷의 index로부터 고정폭 만큼 이동하여 차례대로 검색해 비어 있는 버킷에 데이터를 저장한다.
  2) Quadratic Probing : 해시의 저장순서 폭을 제곱으로 저장하는 방식이다.(충돌 발생 시, 1만큼 이동하고, 계속 충돌 발생 시 2^2, 3^2 ... 의 증가값으로 이동)
  3) Double Hashing Probing : 해시된 값을 한번 더 해싱하여 해시의 규칙성을 없앤다. 다른 기법보다 많은 연산을 요구한다.

• Open Addressing에서 데이터를 삭제하면 삭제된 공간은 dummy space로 활용된다. 그렇기 때문에 해시 테이블을 재정리 해주는 작업이 필요하다.

참고

https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html
https://mangkyu.tistory.com/102