1. 중복순열 구하기
입력값
N:3, M:2 // N은 원소의 개수, M은 뽑을 개수
원소:3,6,9
출력
3 3
3 6
3 9
6 3
6 6
6 9
9 6
9 9
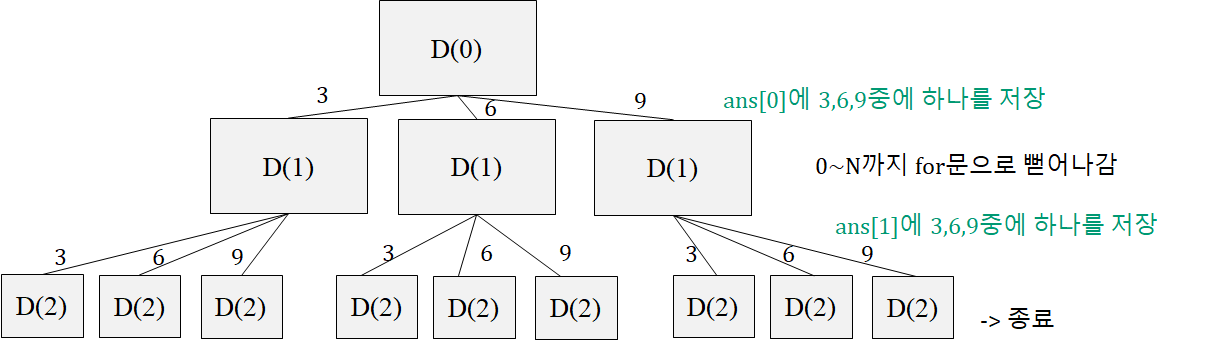
해결방법
- DFS를 활용
- 필요사항
1. arr[n] // 전체 원소를 담을 배열
2. ans[m] // 정답을 넣을 배열
3. static in n;
4. static in m;
5.static ArrayList<ArrayList<Integer>(); - 해결방법 : If (l==m)까지 도착하면 종료, else 안에는 for문을 돌려서 ans배열에 값을 넣어주면 됨.
코드
package inflearn.section8_dfs순열조합;
import java.lang.reflect.Array;
import java.util.*;
public class 중복순열 {
static int arr[];
static int ans[];
static int n;
static int m;
static ArrayList<ArrayList<Integer>>arraylist;
void dfs(int l) {
if (l==m) {
// 출력
ArrayList<Integer>templist= new ArrayList<>();
for (int i=0;i<m;i++) {
templist.add(ans[i]);
}
arraylist.add(templist);
}
else{
for (int i=0;i<n;i++) {
ans[l]=arr[i];
dfs(l+1);
}
}
}
public static void main(String[] args) {
Scanner scan=new Scanner(System.in);
n=scan.nextInt();
m=scan.nextInt();
arr=new int[n];
for (int i=0;i<n;i++) {
arr[i]=scan.nextInt();
}
ans=new int[m];
arraylist=new ArrayList<>();
중복순열 m1=new 중복순열();
m1.dfs(0);
// 정답 출력하는 arraylist
for (int i=0;i< arraylist.size();i++) {
System.out.println(arraylist.get(i));
}
}
}2. 순열 구하기 (순서가 보장된)
입력값
N:3, M:2 // N은 원소의 개수, M은 뽑을 개수
원소:3,6,9
출력
3 6
3 9
6 3
6 9
9 6
해결방법
-
DFS를 활용
-
필요사항
1. arr[n] // 전체 원소를 담을 배열
2. ans[m] // 정답을 넣을 배열
3. check[n] // 체크 배열 필요 사용한것은 또 for문에서 안뻗어 나가기 위해
4. static in n;
5. static in m;
6.static ArrayList<ArrayList<Integer>(); -
해결방법 : If (l==m)까지 도착하면 종료, else 안에는 for문을 돌린다. 이때 주의 점은 If (check[i]==0)를 이용해서 사용하지 않은 원소이면 check[i]=1로 변경해주고 dfs를 돌린다. 그리고 사용한 원소는 다른곳에서 사용되어야 하기 때문에 check[i]=0으로 풀어준다.
-
for문이 도는것은 똑같지만 check배열만 사용한다는 것을 주의하자
방법
-
초기값
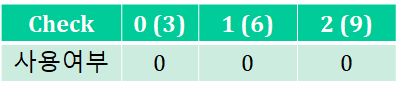
-
D(0)에서 for문으로 뻗어나간다. (사용했으면 1로 체크)
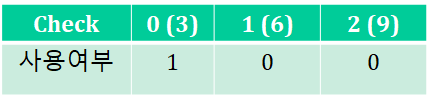
-
D(1)에서 이때 check[0]은 체크되어있으므로 건너뛰고 check[1]을 사용하고 dfs

- 레벨이 2가 되었으므로 출력
- 출력 후 check(1)을 0으로 변경 (다시 사용하게)
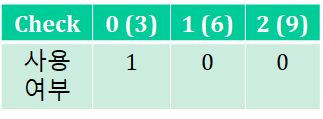
- for문에서 다음꺼를 도는것은 2이므로 2를 체크하고 dfs

- 또 레벨이 2가 되었으므로 출력
- 맨 위 스택으로 가서 6부터 반복적으로 진행
코드
package inflearn.section8_dfs순열조합;
import java.util.ArrayList;
import java.util.Scanner;
public class 순열 {
static int arr[];
static int ans[];
static int check[];
static int n;
static int m;
static ArrayList<ArrayList<Integer>>arraylist;
void dfs(int l) {
if (l==m) {
// 출력
ArrayList<Integer>templist= new ArrayList<>();
for (int i=0;i<m;i++) {
templist.add(ans[i]);
}
arraylist.add(templist);
}
else{
for (int i=0;i<n;i++) {
if (check[i]==0) {
check[i]=1;
ans[l]=arr[i];
dfs(l+1);
check[i]=0; // 다 사용했으면 다시 풀어줌.
}
}
}
}
public static void main(String[] args) {
Scanner scan=new Scanner(System.in);
n=scan.nextInt();
m=scan.nextInt();
arr=new int[n];
for (int i=0;i<n;i++) {
arr[i]=scan.nextInt();
}
ans=new int[m];
check=new int[n];
arraylist=new ArrayList<>();
순열 m1=new 순열();
m1.dfs(0);
// 정답 출력하는 arraylist
for (int i=0;i< arraylist.size();i++) {
System.out.println(arraylist.get(i));
}
}
}3. 조합
입력값
N:3, M:2 // N은 원소의 개수, M은 뽑을 개수
원소:3,6,9
출력
3 6
3 9
6 9
해결방법
- DFS를 이용
- 필요사항
1. arr[n] // 문제 담을 배열- ans[m] // 정답 담을 배열
- 주의사항은 dfs(int l, int s)로 한다. 이유는 s에는 for문이 다음 s+1부터 시작하기 위해 s(start)라는 변수를 넣는다.
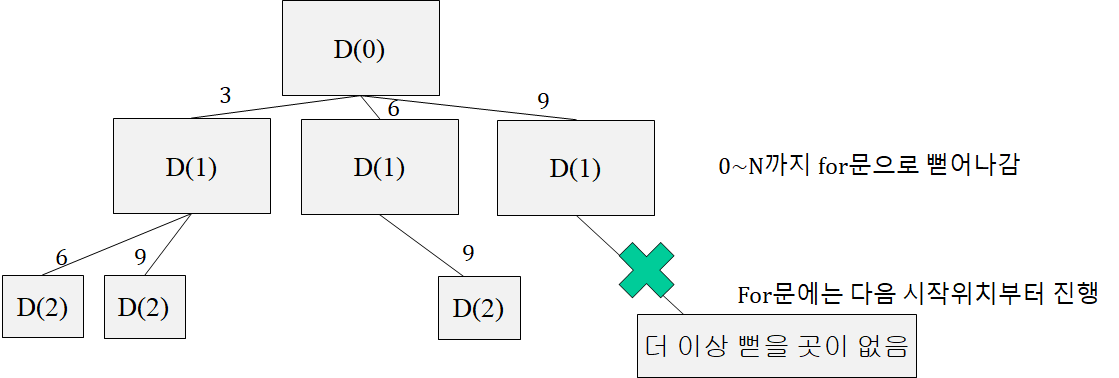
코드
package inflearn.section8_dfs순열조합;
import java.util.*;
public class 조합 {
static int n;
static int m;
static int arr[]; // 문제 담을 배열
static int ans[]; // 정답 담을 배열
static ArrayList<ArrayList<Integer>> arrayList;
void dfs(int l, int s) {
// 출력
ArrayList<Integer> templist=new ArrayList<>();
if (l==m) {
for (int i=0;i<m;i++) {
templist.add(ans[i]);
}
arrayList.add(templist);
}
else {
for (int i=s;i<n;i++) {
ans[l]=arr[i];
dfs(l+1,i+1);
}
}
}
public static void main(String[] args) {
Scanner scan=new Scanner(System.in);
n =scan.nextInt(); //3
m=scan.nextInt(); //2
arr=new int[n]; //n개 담을 문제 담을배열 담음
ans=new int[m]; //m개 담을 정답 배열
for (int i=0;i<n;i++) {
arr[i]=scan.nextInt(); //3,6,9
}
arrayList=new ArrayList<>();
조합 m1=new 조합();
m1.dfs(0,0);
// 출력
for (ArrayList a:arrayList) {
for (int i=0;i<m;i++) {
System.out.print(a.get(i)+" ");
}
System.out.println();
}
}
}4. 조합의 수 구하기
입력
5 3 //
출력
10 //5C3 구하기
해결방법
- Combination의 공식을 이용함
- nCr=n-1Cr-1 + n-1Cr -> DFS에 적용
EX) 5C3=4C2+4C3 ==> 어떻게 이해하냐면 {1,2,3,4,5}가 있을때 5번이 들어간다 안들어간다로 생각, 5번이 들어가면 4명중에 2명을 뽑는 경우 + 5번이 안들어가면 4명중에 3명을 뽄는경우의 수와 같다. - 메모제이션 이용 (2차원 배열을 만들어서 저장한값을 더 뻗지 않고 사용하기 위해 사용)
코드
package inflearn.section8_dfs순열조합;
import java.util.*;
// 12345 // 5C2-> 2개 선택 -> 5는 뽑혔다고 가정 4C1+ 5가 안뽑혔을때 4C2
// nCr= n-1Cr-1 + n-1Cr
public class 조합의경우의수 {
static int n; // n개중에
static int r; // 뽑을 개수
static int dy[][]; // 메모제이션을 기록하기 위한 2차원 배열
static ArrayList<ArrayList<Integer>> arrayList;
public int combi(int n, int r) {
// 메모제이션을 이용해서 이미 수가 차있다면 그대로 사용
if (dy[n][r]>0) return dy[n][r];
// nC0=1, nCn=1이기 때문에 종료 조건
if (r==0 || n==r) return 1;
else {
// return combi(n-1,r-1)+combi(n-1,r);
// 메모제이션 이용
dy[n][r]= combi(n-1,r-1)+combi(n-1,r);
return dy[n][r];
}
}
public static void main(String[] args) {
Scanner scan=new Scanner(System.in);
n=scan.nextInt();
r=scan.nextInt();
dy=new int[35][35]; //최대한 많이 생성
조합의경우의수 m1=new 조합의경우의수();
System.out.println(m1.combi(n,r));
}
}
5. 수열 추측하기

해결방법
-
이항갯수 구하기 : combination의 경우의 수 구하기
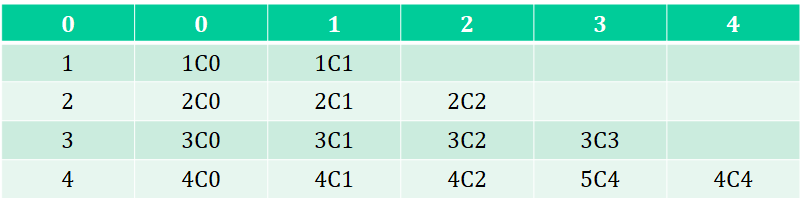
-
모든 순열 만들기 (DFS를 이용해서)
ex)
-
곱해서 m인지 확인
필요사항
- 이항개수
1. dy[][] - 순열
1. check배열 (들어간것을 중복하지 않게 하기 위해
2. arr 배열 (원소가 들어가 있는 배열)
3. ans 배열 (정답이 들어가 있는 배열)
코드
package inflearn.section8_dfs순열조합;
import java.util.*;
public class 수열추측하기 {
// 이항 개수 (combi)
static int bin[][]; //메모제이션
static int b[]; //이항개수를 저장하는 곳 3C0 , 3C1, 3C2, 3C3을 저장하는 곳
static int n;
static int f;
// 순열
static int ans[];
static int[] check;
int combi(int n,int r) {
if (bin[n][r]>0) return bin[n][r];
if (n==r || r==0) return 1;
else {
bin[n][r]=combi(n-1,r-1)+combi(n-1,r);
return bin[n][r];
}
}
void dfs(int l,int sum) {
// 출력
if (l==n) {
if (sum==f) {
// 이 수열이 정답
for (int i=0;i<n;i++) {
System.out.print(ans[i]+" ");
}
System.out.println();
}
else return;
}
else {
for (int i=1;i<=n;i++) {
if (check[i]==0) {
check[i]=1;
ans[l]=i;
dfs(l+1,sum+ans[l]*b[l]);
check[i]=0;
}
}
}
}
public static void main(String[] args) {
Scanner scan=new Scanner(System.in);
n=scan.nextInt();
f=scan.nextInt();
bin=new int[35][35]; // 최대한 크게
b=new int[n+1];
// 3C0, 3C1, 3C2, 3C3을 구해야 됨
수열추측하기 m1=new 수열추측하기();
for (int i=0;i<n;i++) {
b[i]=m1.combi(n-1,i); // 수열을 추측할때는 이항 개수는 3C0 + 3C1 +3C2 +3C3 이기 때문에 1개 적게해서 만들어줌
// System.out.println(m1.combi(n-1,i));
}
// 순열
check=new int[n+1]; // 1부터 시작하므로 +1개 잡음
ans=new int[n+1];
m1.dfs(0,0);
}
}
