약수와 소수

---

약수 : 어떤 수를 나누어 떨어지게 하는 수!
소수 : 1과 그 수를 자신만을 약수로 가지는 수!

소인수분해

---

약수(인수) 중에서 소수인 숫자를 소인수라고 한다.

inputNumber = int(input('1보다 큰 정수 입력: '))

n = 2
while n <= inputNumber:
	if inputNumber % n == 0:
		print('소인수: {}'.format(n))
		inputNumber /= n
	else:
		n += 1

최대공약수

---

두개 이상의 수에서 공통된 약수를 공약수라고 한다.

num1 = int(input("1보다 큰 정수 입력: "))
num2 = int(input("1보다 큰 정수 입력: "))

maxNum = 0

for i in range(1, (num + 1)):
	for num1 % i == 0 and num % i == 0:
			print('공약수: {}'.format(i))
			maxNum = i

print(maxNum)

유클리드호제법

x, y의 최대공약수는 y, r(x%y)의 최대공약수와 같다.

num1 = int(input("1보다 큰 정수 입력: "))
num2 = int(input("1보다 큰 정수 입력: "))

temp1 = num1
temp2 = num2

while temp2 > 0:
	temp = temp2
	temp2 = temp1 % temp2
	temp1 = temp

print(temp1)

최소공배수

---

두 개 이상의 수에서 공통된 배수를 공배수라고 한다.

for문/유클리드호제법 으로 최소공배수 구하기

num1 = int(input("1보다 큰 정수 입력: "))
num2 = int(input("1보다 큰 정수 입력: "))

maxNum = 0

for i in range(1, (num1 + 1)):
		if num1 % 1 == 0 and num2 % i == 0:
				print('공약수: {}'.format(i))
				maxNum = i
print ('최대 공약수: {}'.format(maxNum))

minNum = (num1 * num2) // maxNum
print('최소공배수: {}'.format(minNum))

진법

---

진법이란, 특정 숫자 몇개를 사용하여 수를 표시하는 방법:

기존 함수:

• bin(): 2진수 변환 → 결과는 문자열(0b.....)
• oct(): 8진수 변환 → 결과는 문자열 (0o.....)
• hex(): 16진수 변환 → 결과는 문자열 (0x.....)

#아래 처럼 출력할 수도 있다
print('{0:#b}, {0:#o}, {0:#x}'.format(dNum))

#--------------------------------
print('{}'.format(int('0b11110',2)))
print('{}'.format(int('0o36',8)))
print('{}'.format(int('0x1e',16)))

수열

---

규칙성을 가지고 나열되어 있는 수들

등차 수열:

연속된 두 항의 차이가 일정한 수열

inputN1 = int(input("a1 입력: "))
inputD = int(input("공차 입력: "))
inputN = int(input("n 입력: "))

valueN = 0
n = 1
while n<= inputN:
	if n == 1:
		valueN = inputN1
		print('{}번째 항의 값: {}'.format(n, valueN))
		n += 1
		continue

	valueN += inputD
	print('{}번째 항의 값: {}'.format(n, valueN))
	n += 1

print('{}번째 항의 값: {}'.format(inputN, valueN))

등차 중항

연속된 세 항에서 가운데 항

등차 수열의 합 :

→ Sn = n(a1 + an) / 2

등비 수열 :

연속된 두 항의 비가 일정한 수열

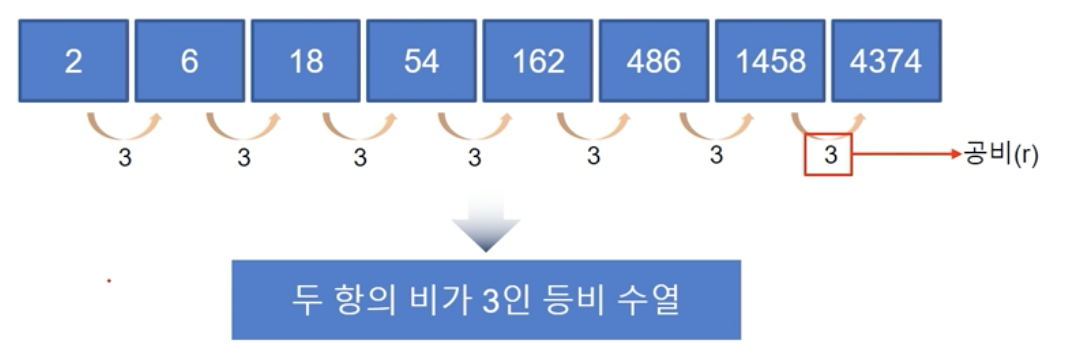
등비수열의 일반항:

등비수열의 합:

a1 = int(input("a1 입력: "))
r = int(input("공비 입력: "))
inputn = int(input("n 입력: "))

valueN = 0
sumN = 0
n = 1
while n <= inputn:
    if n == 1:
        valueN = a1
        sumN += valueN
        print('{}번째 합까지의 합: {}'.format(n, sumN))
        n += 1
        continue
    valueN = valueN * r
    sumN = sumN + valueN
    print('{}번째 합까지의 합: {}'.format(n, sumN))
    n += 1

계차수열

두 항의 차이로 이루어진 또 다른 수열
어떤 수열의 인접하는 두 항의 차로 이루어진 또 다른 수열

inputAN1 = int(input("a1 입력: "))
inputAN = int(input("an 입력: "))

inputBN1 = int(input("b1 입력: "))
inputBD = int(input("bn 공차 입력: "))

valueAN = 0
valueBN = 0

n = 1
while n <= inputAN:
    if n == 1:
        valueAN = inputAN1
        valueBN = inputBN1
        #print('an의 {}번째 항의 값: {}'.format(n, valueAN))
        #print('bn의 {}번째 항의 값: {}'.format(n, valueBN))
        n += 1
        continue

    valueAN = valueAN + valueBN
    valueBN = valueBN + inputBD
    #print('an의 {}번째 항의 값: {}'.format(n, valueAN))
    #print('bn의 {}번째 항의 값: {}'.format(n, valueBN))
    n += 1

print('an의 {}번째 항의 값: {}'.format(n, valueAN))
print('bn의 {}번째 항의 값: {}'.format(n, valueBN))

피보나치 수열

inputN = int(input("n 입력: "))

valueN = 0
sumN = 0

n = 1
while n <= inputN:
    if n == 1 or n == 2:
        valueN = 1
        valuePreN2 = valueN
        valuePreN1 = valueN
        sumN += valueN
        n += 1
    else:
        valueN = valuePreN2 + valuePreN1
        valuePreN2 = valuePreN1
        valuePreN1 = valueN
        sumN += valueN
        n += 1
print('{}번째까지의 총 합: {}'.format(inputN, valueN))

군수열

여러 개의 항을 묶었을 때, 규칙성을 가지는 수열

inputN = int(input("N항 입력: "))

flag = True
n = 1;
nCnt = 1;
searchN = 0

while flag:
    for i in range(1, (n+1)):
        if i == n:
            print('{}'.format(i), end='')
        else:
            print('{}'.format(i), end='')

        nCnt += 1
        if (nCnt > inputN):
            searchN = 1
            flag = False
            break
    print()
    n += 1

---