[Algorithm] 이분 탐색 2

백준 10816 숫자 카드 2

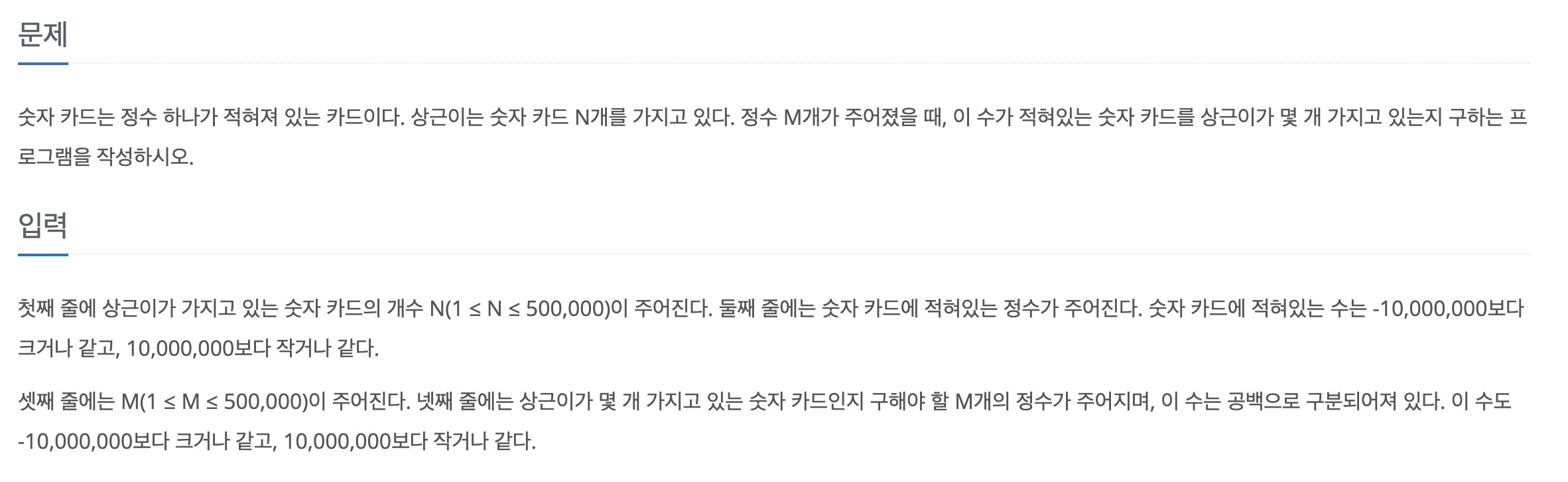
위 문제를 지난번 포스팅때 다룬 기초 이분 탐색을 통해 풀려고 했다. 만약 중복된 수가 있을경우에는 중복된 수의 시작점과 끝지점을 초과하는 지점을 빼서 길이를 제공하면 찾으려는 수의 개수를 구할 수 있는 문제이다.

여기서 궁금한 점은 어떻게 찾는 수의 시작점과 끝점을 초과하는 index 값을 찾는것이였다.

그래서 문제를 풀던 도중 궁금한 점이 생겼다.

int low = 0;
int high = list.size() - 1;

------

int low = 0;
int high = list.size();

지난번 포스팅에는 이분 탐색을 통해 원하는 수의 위치를 찾을땐 전자 경우를 썻다. 하지만 이번 경우에는 후자 선택을 하였다. 왜 이러한 방식을 선택했어야 했을까?

이분탐색의 종료조건

   static int lower_case(List<Integer> numList1, int K) {

        int low = 0;
        int high = numList1.size();


        while (low < high) {
            int mid = low + ((high - low) / 2);

            if (numList1.get(mid) < K) {
                low = mid + 1;
            } else {
                high = mid;
            }
        }

        return low;
    }
    
        static int upper_case(List<Integer> numList1, int K) {

        int low = 0;
        int high = numList1.size();
        while (low < high) {
            int mid = low + ((high - low) / 2);

            if (numList1.get(mid) <= K) {
                low = mid +1;
            } else {
                high = mid;
            }
        }
        return low;
    }

위 코드를 보면 거의 비슷하지만 잘 보면 차이점은 if문안에 등호가 있냐 없냐 차이이다. 내가 이해한바로는 없다면 가장 처음 부분을 찾게 되고 등호가 있다면 중간 값과 찾으려는 값이 같아도 low 를 mid+1로 증가하여 3 3 3 4이 있을경우 0 1 2 번 인덱스에서 0번에서 1번, 1번에서 2번까지 그리고 2번에서 3번까지 인덱스를 찾으며 3번인덱스는 찾으려는 값보다 크므로 찾는값의 초과 인덱스를 반환해준다.

이부분이 핵심인데 만약 high를 size() -1을 하게 된다면 초과 값을 반환하지 못하는 오류를 발생시킬 수 있다. 그렇기에 마지막 인덱스를 넘은 인덱스를 반환할 수 있기때문에 이처럼 반환하는 것이다. 아직 생소한 개념이지만 여러 문제를 풀며 복습하는 시간을 가져보겠다.