[swift] 가장 먼 노드

📌 프로그래머스 LV 3

오늘도 챌린지 성공..! 주말이라 벌써 위기가 찾아왔다...

📝 KeyWord

⇢ BFS : [너비 우선 탐색]
⇢ Graph
⇢ 인접리스트

인접행렬과 인접리스트의 시간복잡도를 체감할 수 있는 문제였다.
Edge를 행렬로 표현할 경우, N개의 노드의 연결 상태를 표현하기위해 "NxN" 배열의 완전탐색이 요구된다. 따라서, Dictionary를 활용한 인접리스트를 구현하여 문제를 해결하였다.

📌 문제풀이

---

⇢ node와 edge의 개수가 큰 범위일 때, 어떻게 해결할 것인가?
⇢ 인접리스트를 어떻게 구현할 것인가?

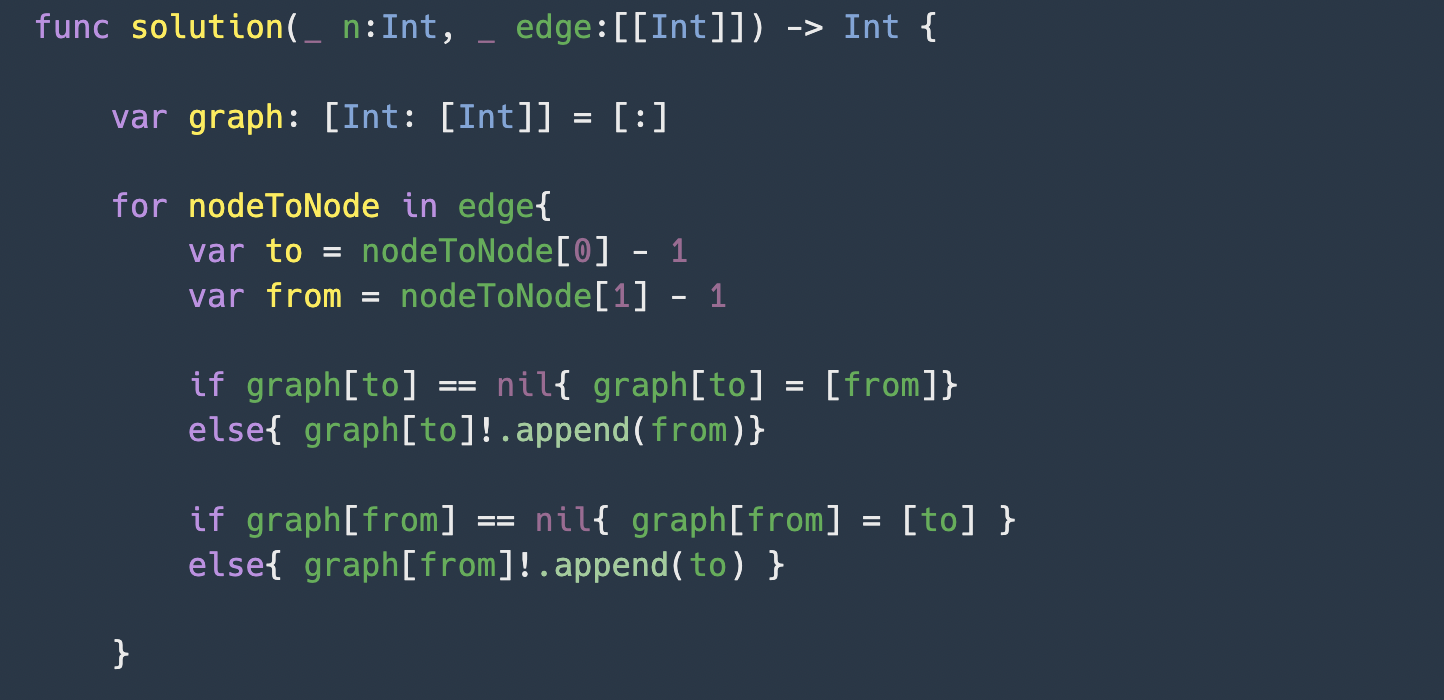
(1) swift의 인접리스트를, graph : [ 노드 : [연결노드]] 형식으로 구현하였다.
(2) 양방향 그래프이므로, "to"와 "from"으로 구분하여 양쪽 노드의 연결관계를 추가.
해당 과정을 통해, 그래프의 인접리스트를 생성하였다. 이제 시작노드부터
인접리스트를 탐색하면서 가장 먼 노드의 개수가 몇 개인지 체크하면 해결할 수 있다.

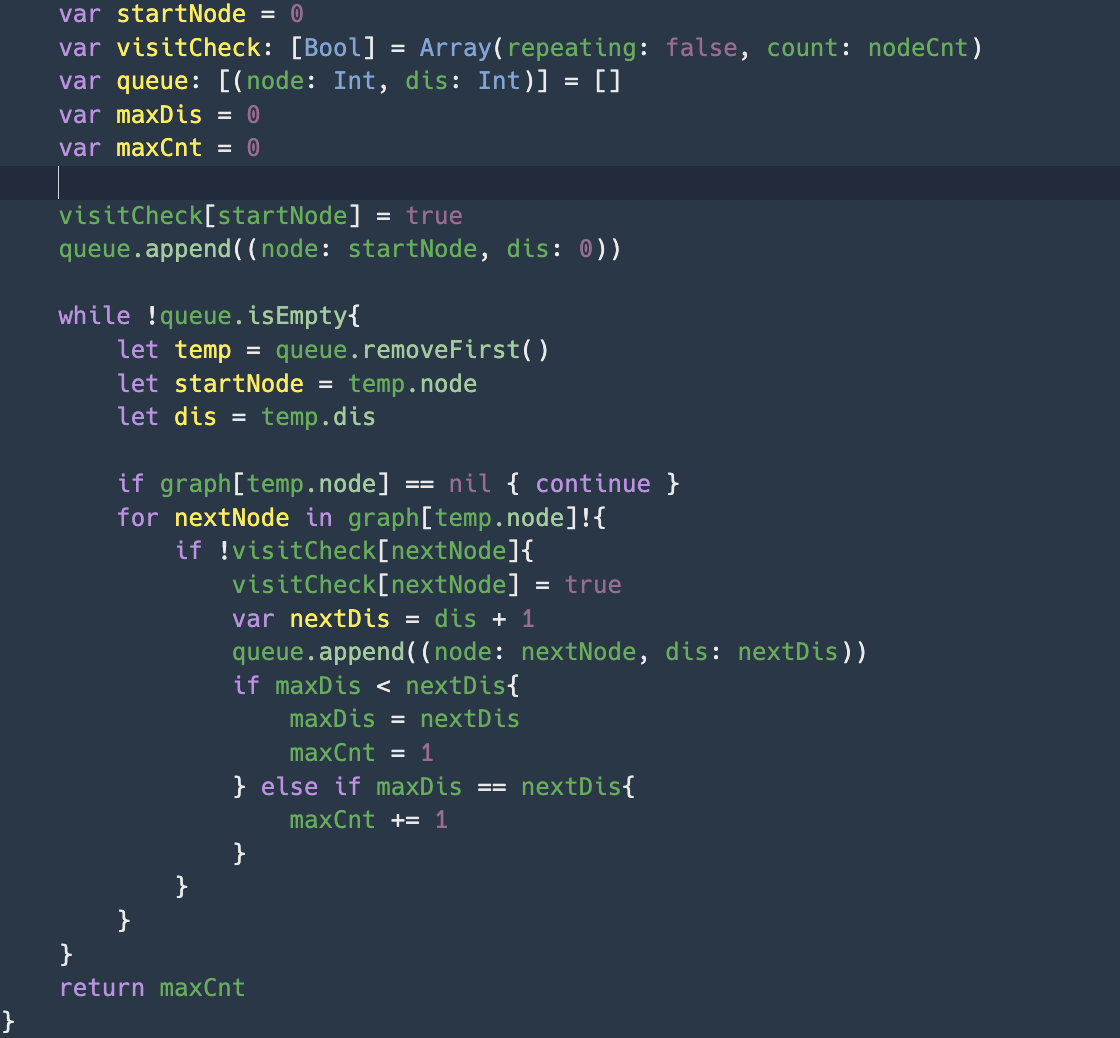
위의 코드는 인접리스트를 탐색하는 BFS 함수 부분이다.
(1) 조건에 따라, 시작노드(startNode)와 초기 거리를 설정한다.
(2) 가장 먼 거리를 측정하기 위한, "maxDis"와 "maxCnt"를 설정한다.
(3) BFS 탐색을 위한 Queue([노드: 시작노드로 부터의 거리])를 설정한다.
(4) 현재 노드로 부터 연결된 노드 거리를 저장하면서, 거리 비교를 통해 노드 개수를 저장.
(5) 가장 먼 노드 개수를 반환한다.

📝 전체코드

import Foundation

func BFS(_ graph: [Int:[Int]], _ nodeCnt: Int) -> Int
{
    var startNode = 0 
    var visitCheck: [Bool] = Array(repeating: false, count: nodeCnt)
    var queue: [(node: Int, dis: Int)] = []
    var maxDis = 0
    var maxCnt = 0
    
    visitCheck[startNode] = true
    queue.append((node: startNode, dis: 0))
    
    while !queue.isEmpty{
        let temp = queue.removeFirst()
        let startNode = temp.node
        let dis = temp.dis
        
        if graph[temp.node] == nil { continue }
        for nextNode in graph[temp.node]!{
            if !visitCheck[nextNode]{
                visitCheck[nextNode] = true
                var nextDis = dis + 1
                queue.append((node: nextNode, dis: nextDis))
                if maxDis < nextDis{
                    maxDis = nextDis
                    maxCnt = 1
                } else if maxDis == nextDis{
                    maxCnt += 1
                }
            }
        }
    }
    return maxCnt     
}



func solution(_ n:Int, _ edge:[[Int]]) -> Int {
    
    var graph: [Int: [Int]] = [:]
    
    for nodeToNode in edge{
        var to = nodeToNode[0] - 1
        var from = nodeToNode[1] - 1
        
        if graph[to] == nil{ graph[to] = [from]}
        else{ graph[to]!.append(from)}
        
        if graph[from] == nil{ graph[from] = [to] }
        else{ graph[from]!.append(to) }
        
    }
    
    
    return BFS(graph, n)
}