문제설명
좌표평면을 좋아하는 진수는 x축과 y축이 직교하는 2차원 좌표평면에 점을 찍으면서 놀고 있습니다. 진수는 두 양의 정수 k, d가 주어질 때 다음과 같이 점을 찍으려 합니다.
- 원점(0, 0)으로부터 x축 방향으로
a*k(a = 0, 1, 2, 3 ...), y축 방향으로b*k(b = 0, 1, 2, 3 ...)만큼 떨어진 위치에 점을 찍습니다. - 원점과 거리가
d를 넘는 위치에는 점을 찍지 않습니다.
예를 들어, k가 2, d가 4인 경우에는 (0, 0), (0, 2), (0, 4), (2, 0), (2, 2), (4, 0) 위치에 점을 찍어 총 6개의 점을 찍습니다.
정수 k와 원점과의 거리를 나타내는 정수 d가 주어졌을 때, 점이 총 몇 개 찍히는지 return 하는 solution 함수를 완성하세요.
제한사항
- 1 ≤
k≤ 1,000,000 - 1 ≤
d≤ 1,000,000
입출력 예
| k | d | result |
|---|---|---|
| 2 | 4 | 6 |
| 1 | 5 | 26 |
입출력 예 설명
입출력 예 #1
- 본문의 예시와 같습니다.
입출력 예 #2
- (0, 0), (0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (1, 0), (1, 1), (1, 2), (1, 3), (1, 4), (2, 0), (2, 1), (2, 2), (2, 3), (2, 4), (3, 0), (3, 1), (3, 2), (3, 3), (3, 4), (4, 0), (4, 1), (4, 2), (4, 3), (5, 0) 위치에 점을 찍을 수 있으며, 총 26개 입니다.
설계 과정
- 가능한 좌표를 넣을 Set만들어두기
- dfs함수를 만들어서 이를 통해 구동
1) 좌표를 넣었을때 원점으로부터의 거리가 d보다 크거나 set에 기존에 있는 것이라면 패스
2) 그게 아니라면 set에 그 좌표 추가하고 answer++해줌.
3) 바로 x+k, y 좌표와 x, y+k 좌표를 dfs 재귀함수를 불러줌,- 만든 함수에 초기값 0,0을 대입
초기 코드
function solution(k, d) {
var answer = 0;
var set = new Set();
function distance(x,y){
return Math.sqrt(x * x + y * y)
}
function dfs(dx,dy){
if(distance(dx,dy)>d || set.has(dx+","+dy)){
return;
}
else{
set.add(dx+","+dy);
answer++;
dfs(dx+k,dy);
dfs(dx,dy+k);
}
}
dfs(0,0);
return answer;
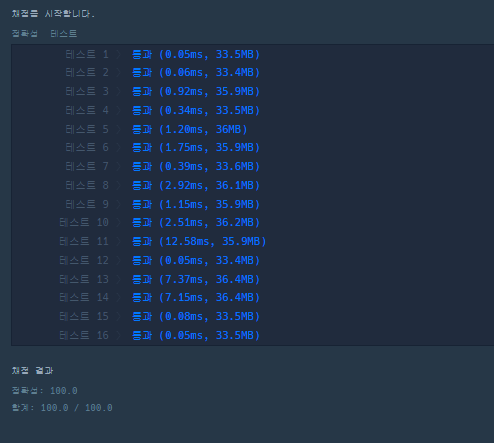
}결과
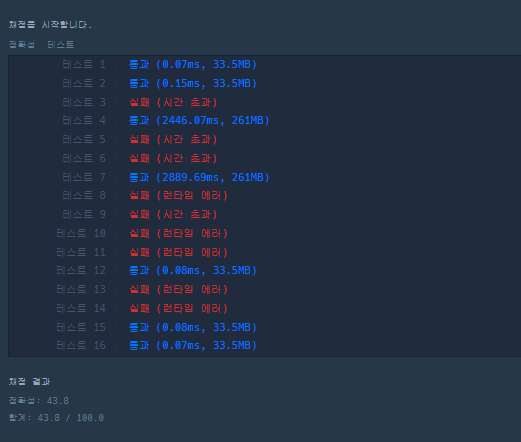
결과는 시간초과가 발생했다...
좀 더 시간복잡도를 개선하는 코드가 필요했다.
재설계 과정
- 우선 yFun을 만들자. 이는 x값을 넣었을때 y가 될 수 있는 최대의 길이를 리턴하는 함수.
- x를 0부터 d까지 k만큼 더해지는 for문 정의
- 여기에 yFun에 x값을 넣어서 최대길이를 뽑아낸 후, 이를 k로 나눈다. 이것이 가능한 점이며, 0일때도 고려하여 1도 추가로 더해준 값을 answer에 더해간다.
정답 코드
function solution(k, d) {
var answer = 0;
function yFun(x){
return (Math.floor(Math.sqrt(d*d-x*x)));
}
for(var x = 0;x<=d;x+=k){
answer+=((Math.floor(yFun(x)/k))+1);
}
return answer;
}결과