선형 회귀 모델

선형 회귀 모델 : 한 선을 먼저 찾기

경사하강법 (Gradient descent) : 경사를 조절하며 최저점(기울기 0)인 점을 찾는 방법

• 한 점을 잡아 미분할 시 그 기울기가 양수인 경우, 점을 왼쪽으로 이동시켜서 기울기를 줄인다
• 만약 그 기울기가 음수인 경우, 점을 오른쪽으로 이동시켜서 기울기를 늘린다

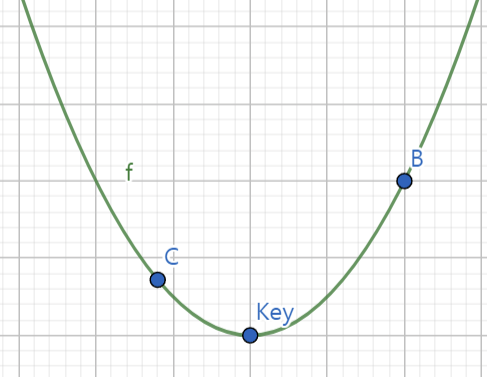
Epoch : 한 그래프의 최소점을 찾기 위해서 움직이는 횟수

• epoch가 클 경우 : 비용이 많이 듦
• epoch가 작을 경우 : 정확도가 낮음

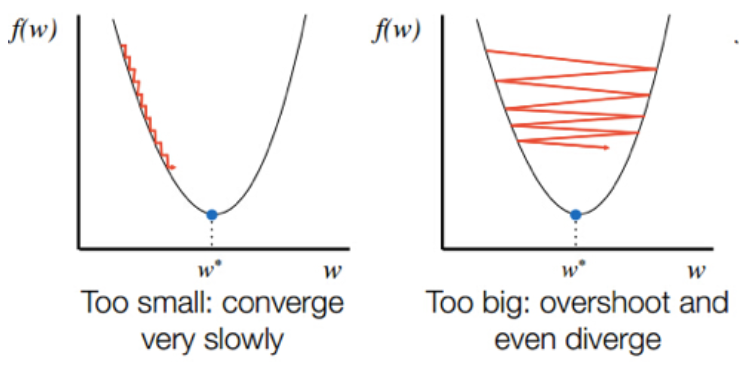
Learning rate : 학습 모델이 학습하는 속도(학습률)

• 학습률이 높은경우 : Cost loss가 발산한다
• 학습률이 낮은 경우 : epoch가 큰 경우와 같이 비용이 많이 듦

경사하강법 코드

#선형 회귀 모델
import numpy as np
import matplotlib.pyplot as plt
x = np.array([2,4,6,8])
y = np.array([81,93,91,97])

plt.scatter(x,y)
plt.show()

a = 0
b = 0

lr = 0.03
epochs = 2001

n = len(x)

for i in range(epochs) :
  y_pred = a * x + b
  error = y - y_pred

  a_diff = (2/n) * sum(-x * (error))
  b_diff = (2/n) * sum(-(error))

a = a - lr * a_diff
b = b - lr * b_diff

if(i % 100 == 0) :
  print("epoch : %.f, 기울기 : %.04f, 절편 : %.04f" % (i,a,b))

y_pred = a * x + b

plt.scatter(x,y)
plt.plot(x, y_pred, 'r')
plt.show()

결과 :

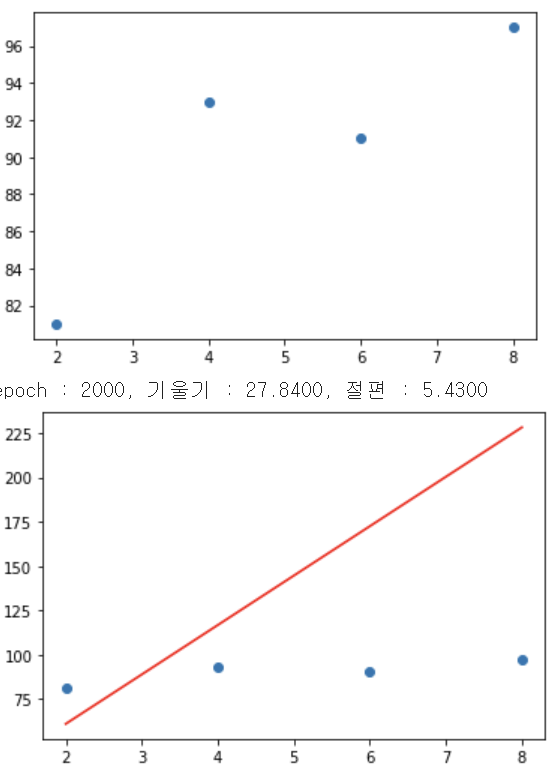
Tensorflow를 사용한 선형회귀

import numpy as np
import matplotlib.pyplot as plt

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

x = np.array([2,4,6,8]) #feature
y = np.array([81,93,91,97]) #target

model = Sequential()

model.add(Dense(1, input_dim = 1, activation = 'linear'))
#출력, 입력, 모델 순으로 입력
model.compile(optimizer='sgd', loss='mse')
#경사하강법(sgd), 평균 제곱 오차(mse) 사용
model.fit(x,y,epochs=2000)

plt.scatter(x,y)
plt.plot(x,model.predict(x),'r')
plt.show()

hour = 7
prediction = model.predict([hour])
print('%.f 시간을 공부할 경우의 예장 점수는 %.2f,점입니다' % (hour,prediction))

결과 :

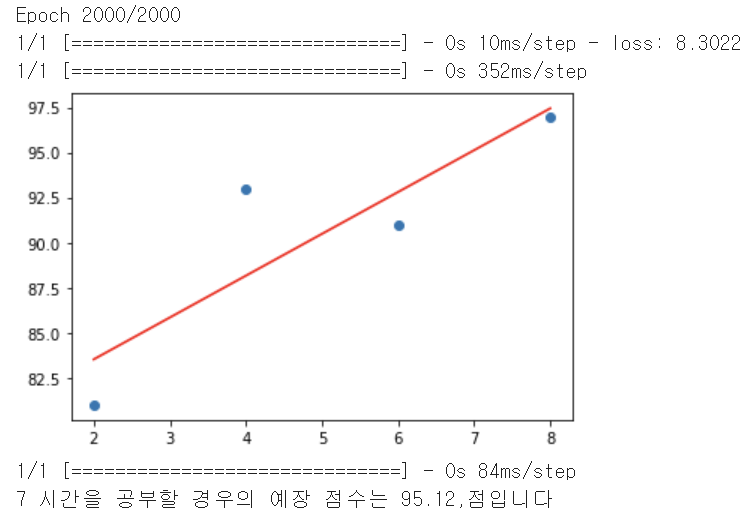
로지스틱 회귀분석(Logistic Regression)

로지스틱 회귀분석(Logistic Regression)

로지스틱 회귀는 수학을 사용하여 두 데이터 요인 간의 관계를 찾는 데이터 분석 기법

이진분류 : 규칙에 따라 입력된 값을 두 그룹으로 분류하는 작업

sigmoid 함수 : 실수 전체를 정의역으로 가지며, 반환값은 단조증가하는 것이 일반적이지만 단조감소할 수도 있다

• cross-entropy error(딥러닝 손실함수, 정보량이 0에 가까워져서 정답확률이 1에 수렴하는 것을 목표로 함)를 사용

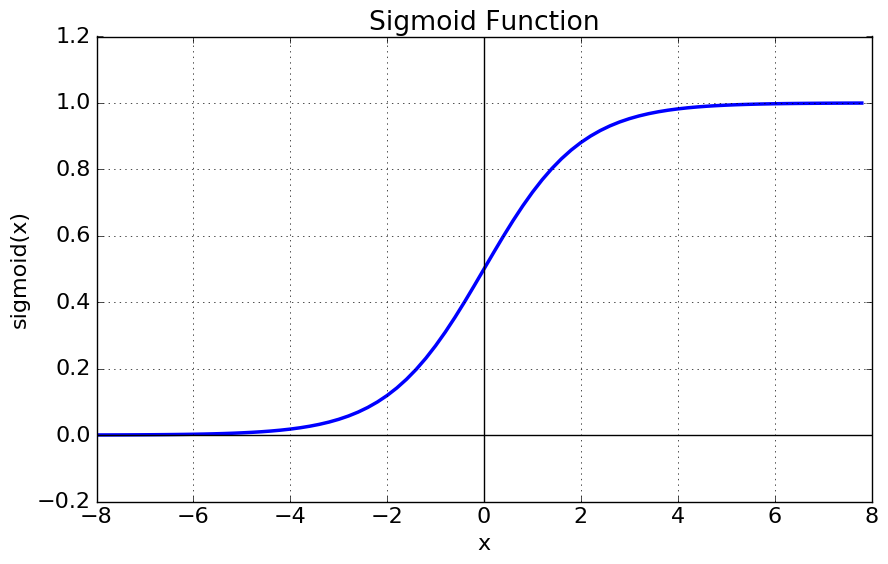
시그모이드 함수 코드

import numpy as np
import matplotlib.pyplot as plt

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

x = np.array([2, 4, 6, 8, 10, 12, 14]) #Feature
y = np.array([0, 0, 0, 1, 1, 1, 1]) #Target

model = Sequential()

model.add(Dense(1, input_dim = 1, activation='sigmoid'))

model.compile(optimizer='sgd', loss='binary_crossentropy') 

model.fit(x, y, epochs = 5000) 

plt.scatter(x, y)
plt.plot(x, model.predict(x), 'r')
plt.show()

hour = 7
prediction = model.predict([hour])

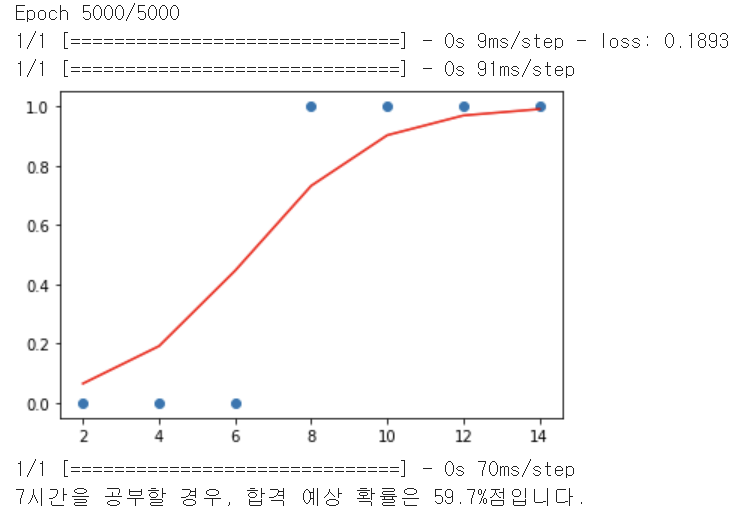
print("%.f시간을 공부할 경우, 합격 예상 확률은 %.01f%%점입니다." %(hour, prediction * 100))

결과 :