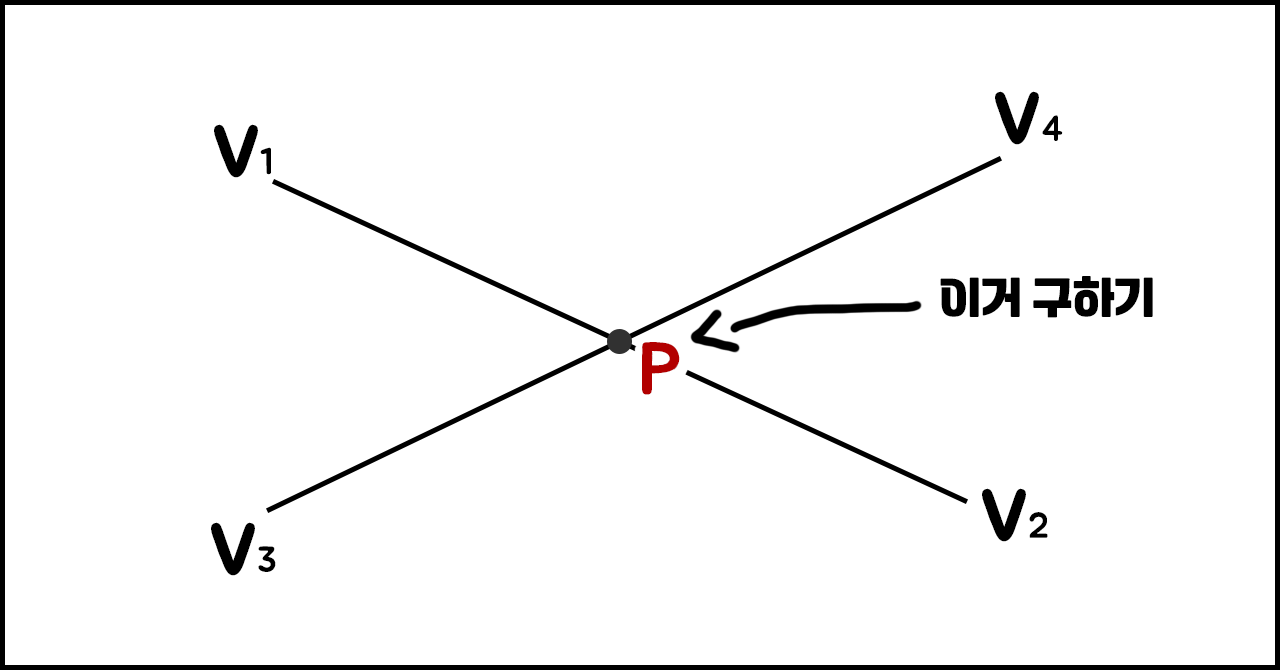
선분의 교점 구하기
게임을 개발하다 기능 구현을 위해 두 벡터(시점과 종점)로 이루어진 두 선분의 교점을 구해야 하는 상황이 생겼다. 여러 가지 방법들 중 벡터의 외적을 사용한 방법이 인상 깊어 이에 대해 이해해 보고 정리해 보려 한다.
문제 분석
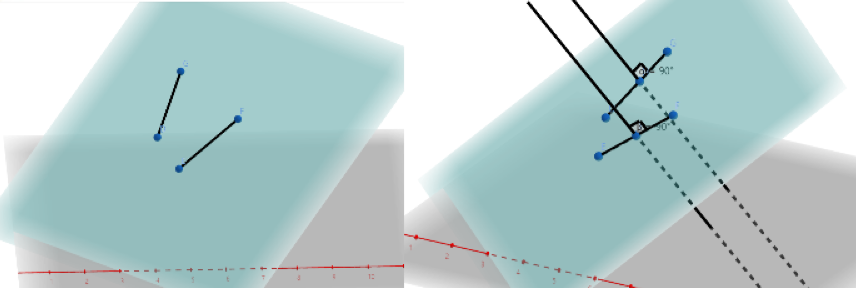
시점과 종점으로 이루어진 두개의 선분 I와 J가 주어진다.
선분 I는 두 벡터 a와 b, 선분 J는 두 벡터 c와 d로 이루어져 있다.
이 때 I와 J가 만나는지, 만약 만난다면 그 교점을 구하시오.이 문제의 중점은 '선분'의 교점이다.
선분 I와 J를 직선으로 본다면 이 두 직선의 평행하지 않은 경우 교점은 무조건 존재하기 때문이다.
따라서 다음과 같은 순서로 문제를 해결한다.
- 직선 I'과 직선 J'의 교점 구하기
- 해당 교점이 선분 I와 J위에 있는지 판별하기
두 직선의 교점 구하기
1. 아핀 공간 활용
계산을 보다 편하게 하기 위하여 '아핀 공간'을 활용할 것이다.
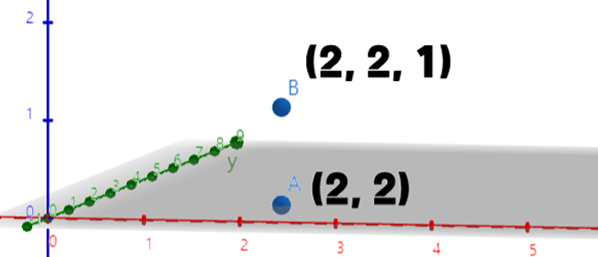
두 직선의 교점을 구하는 과정에선 아핀 공간에 대해 세세하게 알 필요까진 없음으로 그냥 한 차원을 증가시켜 1로 고정시킨다는 것만 알아두자.
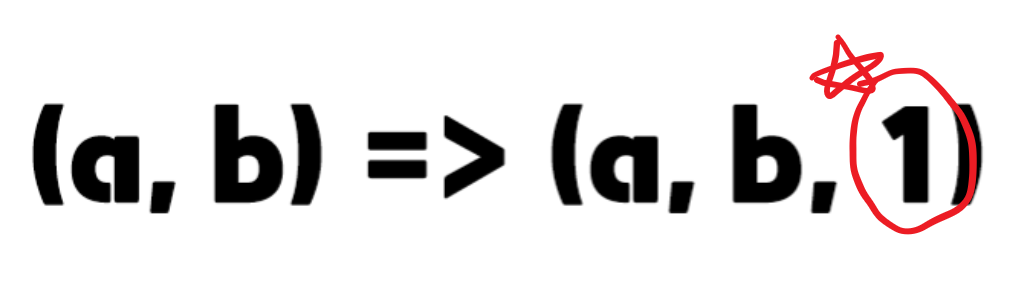
그림으로 보았을 땐 다음과 같다.
코드
a.z = 1; b.z = 1; c.z = 1; d.z = 1;
2. 두 점과 두 점의 수직벡터가 이루는 평면
두 점과 평면의 방향을 알면 평면을 그릴 수 있다.
이 때 선분을 이루는 두 벡터를 두 점으로,
그 두 벡터의 외적, 즉 두 벡터의 수직 벡터를 방향으로 두어 평면을 그리면 다음과 같이 나온다.
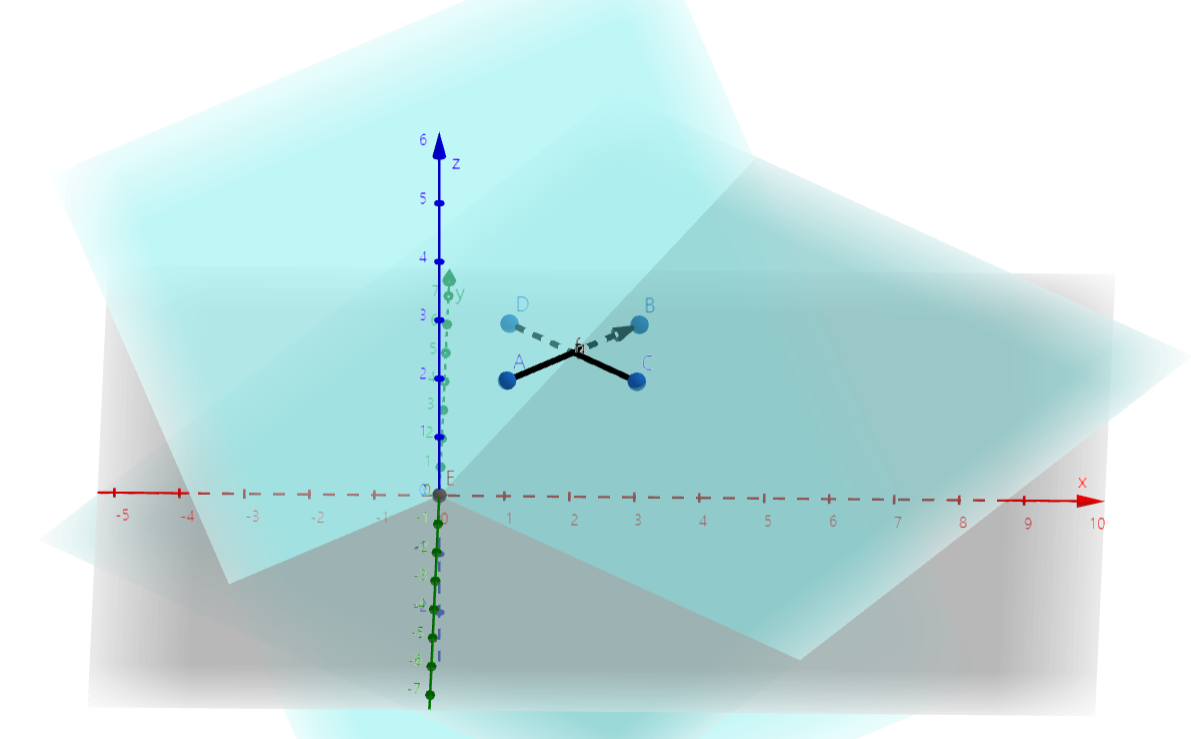
A, B, C, D 모두 아핀 공간이라는 개념을 활용하기 위해 한 차원 증가시켜 1로 고정시켰기에 다음과 같은 두 평면이 그려진다.
그림에서 알 수 있듯이 우리가 구해야 하는 것은 저 두 평면의 교선이다.
해당 교선은 원점과 두 선분의 교점을 지나는 직선이다.
저 교선을 구하기 위해선 평면의 성질과 외적에 대해 알아야 한다.
코드
plane1 = cross(a, b); plane2 = cross(c, d);
3. 평면 위의 선분, 그리고 외적
평면 위에 어느 선을 긋던 평면의 방향인 벡터와는 무조건 수직일 수 밖에 없다.
교선이라 함은 두 평면에 모두 속해있는 직선이다.
따라서 앞서 언급한 평면의 성질을 생각해보면 교선이라는 것은 두 평면의 방향과 동시에 수직인 직선이라 말할 수 있다.
따라서 해당 교선을 구하기 위해선 두 평면의 방향과 동시에 수직인 직선을 구하면 된다.
두 평면의 방향은 앞서 외적을 통해 구한 두 수직 벡터이다.
그럼 두 벡터와 동시에 수직인 직선(벡터)은 어떻게 구할까?
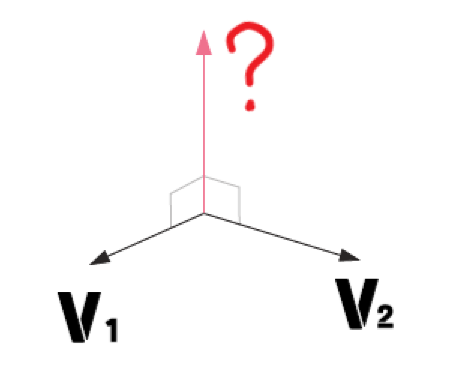
바로 외적을 사용하면 된다.
두 벡터를 외적하면 두 벡터의 수직인 벡터를 구할 수 있다.
따라서 두 평면의 방향을 외적하면 두 평면과 동시에 수직인, 즉 구하고자 하는 교선을 얻을 수 있다.
코드
lineIntersection = cross(plane1, plane2);
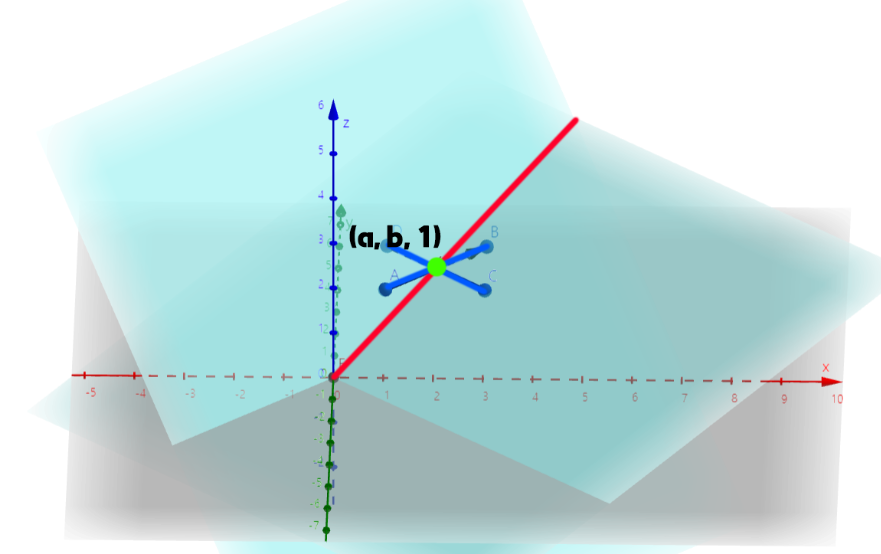
4. 직선과 z = 1 평면의 교점
우린 2차원 벡터를 한 차원 증가시켜 3차원의 관점으로 계산을 진행했기에 앞서 구한 교선은 3차원 상에서의 직선일 것이다.
하지만 우린 2차원 벡터를 무작정 한 차원 증가시킨 것이 아닌 마지막 차원, 즉 z 좌표를 1로 고정했다.
따라서 구한 교선이 z = 1 을 지날 때의 점이 바로 두 직선의 교점이다.
코드
// 얘가 1인 시점을 구해야 함. 즉 모든 원소를 z로 나눈다. z = lineIntersection.z; x = lineIntersection.x / z; y = lineIntersection.y / z; pointIntersection = (x, y);
위와 같은 과정을 통해 두 선분을 직선으로 보았을 때의 교점을 구했다.
구한 두 직선의 교점이 두 선분의 교점인지 확인하기 위해선 해당 교점이 두 선분 위에 있는지만 확인하면 된다.
교점이 선분 위에 있는지 판별하기
1. 방향 판별
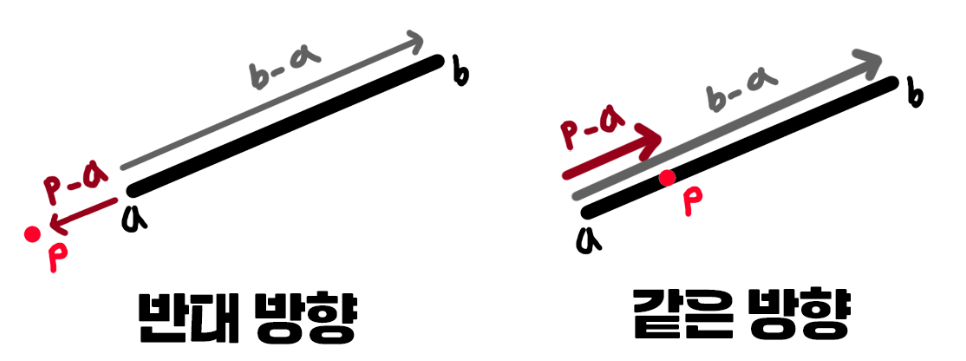
두 벡터 a, b로 이루어진 선분과 점 p가 있다고 하자.
우선 점 p가 선분 ab에 위에 있기 위해선
p - a 의 방향과 b - a 의 방향이 같아야 한다.
(a와 b가 바뀌어도 무관)
코드
distance = p - a; length = b - a; if (distance.normalized != length.normalized) return false;
2. 거리 판별
하지만 방향이 같더라도 선분 밖에 점인 경우를 판별해야 한다.
점이 선분 안에 존재하기 위해선 a와 p의 거리가 선분의 길이를 넘지 않아야 한다.

코드
if(distance.magnitude > length.magnitude) return false;
전체 코드
위 과정을 코드로 나타내면 다음과 같다.
(UNITY + C#)
// 0 근사값
public const float EPSILON = 0.01f;
// 두 선분의 교점을 찾는 함수
public bool GetSegmentIntersection(Vector3 a, Vector3 b, Vector3 c, Vector3 d, out Vector3 intersection)
{
// false 가 반환된 경우 두 선분이 평행 또는 동일하다
// 두 선분 동일한 경우 => 교점을 찾을 수 없음
// 두 선분 평행한 경우 => 한 점에서 닿았을 때만 교차한다 O
if(GetLineIntersection(a, b, c, d, out intersection) == false)
return GetParallelTangent(a, b, c, d, out intersection); // 한 점에 닿았을 경우 교점을 구하는 함수
// 직선의 교점이 선분 A와 선분 B 위에 있으면 true 반환
return (intersection.InnerSegment(a, b) && intersection.InnerSegment(c, d));
}
// 두 직선의 교점을 찾는 함수
public bool GetLineIntersection(Vector3 a, Vector3 b, Vector3 c, Vector3 d, out Vector3 intersection)
{
a.z = b.z = c.z = d.z = 1;
Vector3 plane1 = Vector3.Cross(a, b);
Vector3 plane2 = Vector3.Cross(c, d);
Vector3 line = Vector3.Cross(plane1, plane2);
if (Mathf.Abs(line.z) < EPSILON)
{
intersection = Vector3.zero;
return false; // 두 선분이 평행 또는 동일할 때는 false 반환
}
// line(두 평면의 교선) = (x, y, w)
// 교점 = (x / w, y / w)
intersection = new Vector3(line.x / line.z, line.y / line.z);
return true; // 교점이 찾아지면 true 반환
}
private bool GetParallelTangent(Vector3 a, Vector3 b, Vector3 c, Vector3 d, out Vector3 intersection)
{
intersection = Vector3.zero;
// a를 시점으로 b를 종점으로 고정
if(b.x < a.x && b.y < a.y)
{
Vector3 temp = b;
b = a;
a = temp;
}
// c를 시점으로 d를 종점으로 고정
if(d.x < c.x && d.y < c.y)
{
Vector3 temp = d;
d = c;
c = temp;
}
// 점 c를 기준으로 a와 b를 외적했을 때 값이 0이 아니면 평행하지 않다
// 그렇게 됐을 때 선분 A와 선분 B는 동일선상에 있지 않다
if(c.CCW(a, b) != EPSILON)
return false; // 선분 A와 선분 B는 동일선상에 있지 않을 때 교점을 찾을 수 없기 때문에 false 반환
// 동일선상에 있지만 모든 꼭짓점들이 같은 경우 동일한 직선이다
if(b == c && d == a)
return false; // 동일한 직선일 경우 교점을 찾을 수 없기 때문에 false 반환
if(b == c) // 선분 A의 종점과 선분 B의 시점이 같을 경우 교점은 b(선분 A의 종점)와 c(선분 B의 시점)
intersection = b;
if(d == a) // 선분 B의 종점과 선분 A의 시점이 같을 경우 교점은 d(선분 B의 종점)와 a(선분 A의 시점)
intersection = d;
Debug.Log(intersection);
return true; // 교점이 찾아졌을 때 true 반환
}
public static bool InnerSegment(this Vector3 point, Vector3 a, Vector3 b)
{
Vector3 v1 = point - a; // a -> point 벡터
Vector3 v2 = b - a; // a -> b 벡터
if (v1.normalized == v2.normalized)
{
if(v1.sqrMagnitude <= v2.sqrMagnitude)
return true; // true 반환
}
return false; // 점이 선분 밖에 위치한다면 false 반환
}
// 원점으로 부터 a -> b 반시계방향 판별
public float CCW(Vector3 a, Vector3 b) => Vector3.Cross(a, b).z;
// point로 부터 a -> b 반시계방향 판별
public static float CCW(this Vector3 point, Vector3 a, Vector3 b) => Vector3.Cross(a - point, b - point).z;