<재귀>

자기 자신을 다시 호출하는 형식

• 큰 문제를 해결하기 위해 동일한 유형의 더 작은 문제로 나누는 방식
• 완전탐색을 잘 하기 위해 재귀를 배운다~!
  
  
• 기저 조건(base case) : 더 이상 나눌 수 없는 가장 작은 문제, 재귀 호출X, 직접 결과 반환
• 재귀 호출(recursive call) : 더 작은 문제로 나누고 그 문제를 해결하기 위해 함수를 다시 호출
  • 재귀를 구현할 때 점화식을 세우는 것이 중요

1) 예시

팩토리얼

public static int factorial(int n) {
    if(n == 1) {
        return 1;
    }
    return n * factorial(n - 1);
}

피보나치 수열

public static int fibonacci(int n) {
   if(n == 1 | n == 2) {
       return 1;
   }
   return fibonacci(n - 1) + fibonacci(n - 2);
}

2) 문제적용

• 완전 탐색
  
• 동적 계획법(DP)
  
• DFS

---

<✨완전 탐색>

가능한 모든 경우의 수를 탐색

• 시간 복잡도가 매우 높아질 수 있음

1) 문제 적용

• 모든 가능성 탐색(브루트 포스)
  
• 백트래킹
  
• 순열/조합/부분집합
  
• 격자 탐색(DFS, BFS)
  • 격자 내의 모든 위치 탐색하여 특정 조건을 만족하는 위치 찾기

2) 백트래킹

모든 가능성을 의사결정 트래 형태로 구성하여 재귀적으로 탐색

• 가능성 없는 경로는 미리 가지치기(pruning)하여 성능 향상
• 보통 백트랙킹은 조건문으로 표현, 특정 조건을 만족하면 return

Q. 가로/세로를 이어서 "CAT"이라는 글자 만들기

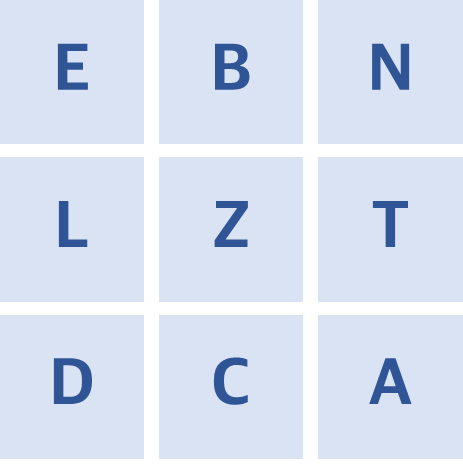
//슈도코드
function backtrack(상태):
	if 특정 조건 만족 : //base case
    	해답O -> 결과 저장 / 출력
        return
   	for 가능한 모든 선택지 in 현재 상태:
    	if 선택지 가능성 X:
        	continue //가지치기
        선택지 적용
        backtrack(새로운상태) //재귀
        선택지 되돌리기

---

<순열(Permutation)>

n개의 원소 중 r개의 원소를 선택하여 순서있게 선택
$P(n,r)=\frac{n!}{(n-r)!}$

import java.util.*;
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        boolean[] visited = new boolean[nums.length];

        backtrack(new ArrayList<>(), nums, visited, result);

        return result;
    }

    // 순열 만들어서 result에 추가
    void backtrack(List<Integer> current, int[] nums, boolean[] visited, List<List<Integer>> result) {
        //basecase
        if(current.size() == nums.length) {
            result.add(new ArrayList<>(current)); //배열: 참조, current를 추가하면 current값 바뀔 때 얘도 바뀜
            return;
        }

        //recursive call
        for(int i = 0; i < nums.length; i++) {
            if(visited[i]) {
                continue; //방문했으면 건너뛰기
            }
            current.add(nums[i]); //추가
            visited[i] = true;
            backtrack(current, nums, visited, result);
            current.remove(current.size() - 1); //마지막 원소 제거
            visited[i] = false;
        }
    }
}

---

<조합(Combination)>

n개의 원소 중 r개의 원소를 순서 상관없이 선택
$C(n,r)=\begin{pmatrix}n\\r\\ \end{pmatrix}=\frac{n!}{r!\times(n-r)!}$

• visited? ➔ X - 중복되면 안되고 i보다 큰 숫자들만 선택하면 됨

import java.util.*;
class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> result = new ArrayList<>();
        boolean[] visited = new boolean[n];

        backtrack(1, new ArrayList<>(), n, k, result);

        return result;
    }

    void backtrack(int start, List<Integer> current, int n, int k, List<List<Integer>> result) {
        //basecase
        if(current.size() == k) {
            result.add(new ArrayList<>(current));
            return;
        }

        //recursive call
        for(int i = start; i <= n; i++) {
            current.add(i);
            backtrack(i + 1, current, n, k, result);
            current.remove(current.size() - 1);
        }
    }
 }

Two Sum