🧐 문제 설명

😍 나의 풀이
처음에 무방향성 그래프인 줄 모르고 방향을 고려하다가 좀 헤맸다..🤣
DFS나 BFS로 풀이하기 위해서 node 간 연결관계를 표현하는 방법은 크게 두가지인 것 같다. 그래프로 표현하기 혹은 딕셔너리로 표현하기.
노드 연결관계만 표현되고 나면 DFS는 재귀를 이용해서 방문하지 않은 곳이면, 방문 처리를 해주면 된다!
위 문제에서는 입출력 예시로 노드가 1~7번이기 때문에 인덱스와 노드 이름을 같게 매칭하기 위해서 방문 처리할 리스트인 visited와 그래프 리스트 모두 (노드 크기+1)만큼의 사이즈로 만들었다.
→ 인덱스 0부터 시작이 아니라 1~7 인덱스로 만들기 위해서~
웜 바이러스에 감염된 컴퓨터의 수는 시작 노드는 제외하기 때문에 방문 처리된 것들 중에 1을 빼주면 정답이다.
node = int(input())
edge = int(input())
visited = [False] * (node+1)
graph = [[] for i in range(node+1)]
for i in range(edge):
start, end = map(int, input().split())
graph[start].append(end)
graph[end].append(start)
def dfs(start, graph, visited):
visited[start] = True
for i in graph[start]:
if (visited[i] == False):
dfs(i, graph, visited)
return visited.count(1) - 1
print(dfs(1, graph, visited))👏 다른 사람의 풀이
BFS 풀이
from _collections import deque
def bfs(vertex):
# 속도가 빠른 디큐를 사용해서 BFS 탐색
q = deque()
q.append(vertex)
# 시작점 방문 체크를 True로 해준다음
visit[vertex] = True
while q:
# 큐에 쌓인 노드들 중에서 하나를 꺼내고
current = q.popleft()
# 노드에 인접한 이웃들중
for neighbor in adj[current]:
# 방문하지 않은 노드를
if visit[neighbor] is False:
# q에 쌓고, 방문 체크를 True로 해준다.
q.append(neighbor)
visit[neighbor] = True
return
n = int(input())
m = int(input())
adj = [[] for _ in range(n+1)]
# 인접 리스트 생성 | 방향없는 그래프
for _ in range(m):
a, b = map(int, input().split())
adj[a].append(b)
adj[b].append(a)
# 방문 배열 사용
visit = [False]*(n+1)
cnt = 0
# 1번부터 시작
bfs(1)
# 결과는 visit 배열에 True의 갯수를 세준다.
print(visit.count(True)-1)🥇 Today I Learn
그래프 (Graph)
- 정점(node)과 간선(edge)으로 각 정점들의 관계를 나타낸 자료 구조
방향성 그래프
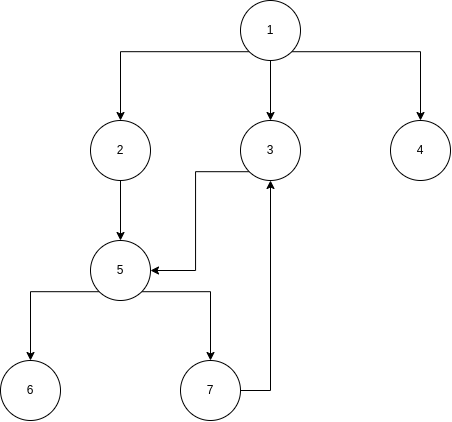
만약 위와 같이 그래프가 주어진다면,
1은 2, 3, 4 와 연결되어 있고,
2는 5와 연결되어 있고,
3도 5와,
5는 6, 7과,
7은 3과 연결되어 있음을 확인할 수 있다
graph = {1 : [2, 3, 4], 2 : [5], 3 : [5], 4 : [],
5 : [6, 7], 6 : [], 7 : [3]}→ 파이썬에서 그래프는 딕셔너리를 이용해서 풀이
무방향성 그래프
#만약 n개만큼의 정점이 존재하고, m개만큼의 입력을 받는다면
graph = [[] for _ in range(n+1)] # n+1개만큼의 공간을 만들어서 graph[n]이 n번 정점을 나타내도록 해 준다
for _ in range(m):
x,y = map(int,input().split()) #만약 1 2를 입력받으면
graph[x].append(y) # 1번 정점에 2를 넣어주고 -> graph[1] = [2]
graph[y].append(x) # 2번 정점에 1을 넣어준다 -> graph[2] = [1]→ 그래프는 (정점 수) 혹은 (정점 수 +1) 만큼의 공간을 미리 만들고,
무방향성이기 때문에 시작 정점에 요소가 추가되면 종료 정점에도 요소가 추가되어야 한다.

