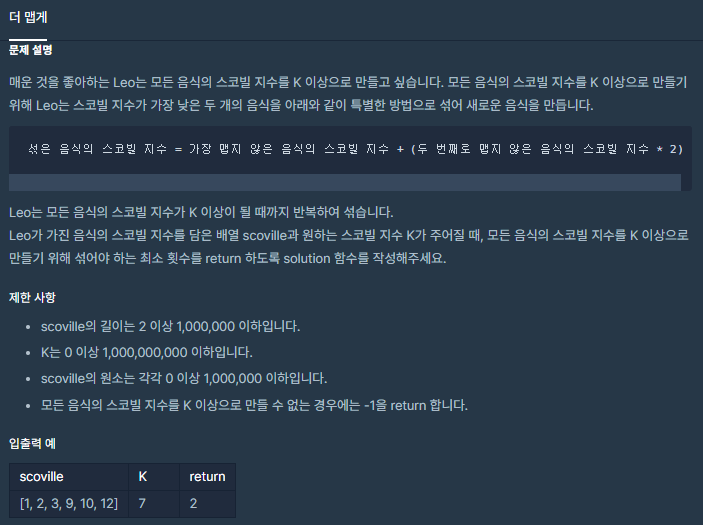
🧐 문제 설명
😍 나의 풀이
최소값과 그 다음 최소값을 이용하는 문제여서 힙정렬을 이용하기로 했다. 파이썬은 heapq 모듈(기본이 최소힙)을 제공하기 때문에 쉽게 힙을 만들 수 있다. 이 문제도 힙을 사용하는 방법만 알면 쉽게 문제를 풀 수 있는데 다음 조건은 생각해봐야하는 점이다.
- 모든 음식의 스코빌 지수를 K 이상으로 만들 수 없는 경우에는 -1을 return 합니다.
예를 들어, scoville 리스트가 [0,0,0,0] 으로 아무리 힙을 이용한 계산과정을 반복해도 K를 넘을 수 없는 case 혹은 K값이 너무 크게 주어져서 계산을 계속 해도 K를 넘을 수 없는 case가 존재한다.
즉 이 문제는 힙에서 최소 원소를 두 개 빼서 연산 후 그 계산 값을 힙에 넣는 과정을 반복하다보면, 힙의 원소가 1개씩 계속 줄어드는 상황이 발생한다. 이 때, 힙이 더 이상 연산을 할 수 없는 원소 갯수가 되었을 때도 남아 있는 원소들이 모두 K를 넘지 않으면 -1을 return하면 된다.
위 문제에서는 heappop()을 2번 수행해야하는데 힙의 길이가 2보다 작게 되면 더 이상 연산을 수행할 수 없으므로 그때도 최솟값이 K를 못 넘는다면 -1을 반환하도록 했다.
import heapq
def solution(scoville, K):
count = 0
heapq.heapify(scoville) #리스트를 힙으로 변환
while scoville[0] < K:
new = heapq.heappop(scoville) + heapq.heappop(scoville) * 2
heapq.heappush(scoville, new)
count +=1
if scoville[0] < K and len(scoville) < 2 :
return -1
return count👏 다른 사람의 풀이
대부분 heapq 모듈을 사용해서 풀어서 크게 다른 코드는 없지만, 위에서 말한 조건을 처리하는 과정에서 힙의 참조할 수 없는 인덱스에 대해서 try-except로 처리한 것이 깔끔해보여서 긁어왔다.
def solution(scoville, k):
import heapq
heap = []
for num in scoville:
heapq.heappush(heap, num)
mix_cnt = 0
while heap[0] < k:
try:
heapq.heappush(heap, heapq.heappop(heap) + (heapq.heappop(heap) * 2))
except IndexError:
return -1
mix_cnt += 1
return mix_cnt🥇 Today I Learn
heapq module
파이썬에서 제공하는 힙큐 모듈, 일반적인 리스트를 최소 힙처럼 다룰 수 있음
힙에 원소 추가 : heappush(힙, 원소)
heapq.heappush(heap, 4)
heapq.heappush(heap, 1)
heapq.heappush(heap, 7)
heapq.heappush(heap, 3)
print(heap)
-----------------------
[1, 3, 7, 4] # 결과힙에 원소 삭제 : heappop(힙)
원소를 삭제할 대상 리스트를 인자로 넘기면, 가장 작은 원소(최솟값)를 삭제 후에 그 값을 리턴
print(heapq.heappop(heap))
print(heap)
--------------------------
1
[3, 7, 4] # 결과힙의 최솟값 삭제없이 접근 : 힙[0]
print(heap[0])기존 리스트를 힙으로 변환 : heapify(리스트)
heap = [4, 1, 7, 3, 8, 5]
heapq.heapify(heap)
print(heap)
-------------------------
[1, 3, 5, 4, 8, 7][응용] K번째 최소값/최대값
K번째 최소값을 구하기 위해서는 주어진 배열로 힙을 만든 후, heappop() 함수를 K번 호출
[응용] 최대 힙
heapq 모듈은 최소 힙(min heap)만 동작하기 때문에 최대 힙(max heap)으로 활용하려면 힙에 튜플(tuple)를 원소로 추가하거나 삭제하면, 튜플 내에서 맨 앞에 있는 값을 기준으로 최소 힙이 구성되는 원리를 이용
따라서 최대 힙을 만들려면 각 값에 대한 우선 순위를 구한 후, (우선 순위, 값) 구조의 튜플(tuple)을 힙에 추가하거나 삭제! 힙에서 값을 읽어올 때는 각 튜플에서 인덱스 1에 있는 값 이용
import heapq
nums = [4, 1, 7, 3, 8, 5]
heap = []
for num in nums:
heapq.heappush(heap, (-num, num)) # (우선 순위, 값)
while heap:
print(heapq.heappop(heap)[1]) # index 1
--------------------------------------------
8
7
5
4
3
1 #결과
