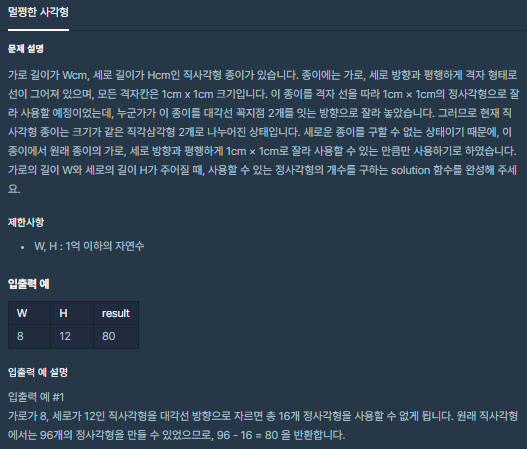
🧐 문제 설명
😍 나의 풀이
우선, 처음에는 좌표평면을 이용한 풀이를 고려했다. 대각선을 직선의 방정식으로 표현해서 x, y를 가로, 세로 크기만큼 반복문을 돌면서 교점을 파악하면 될 것 같았다.
하지만 이 방식은 W와 H가 1억 이하의 자연수였기 때문에, x, y에 대해 이중 for문이 돈다고 하면 100000000 * 100000000의 시간복잡도가 나와서 이렇게 푸는 방식은 안될거라고 생각했다.
그래서, W와 H로 그려지는 사각형에 어떤 규칙이 있을거라고 생각하고 접근했다.
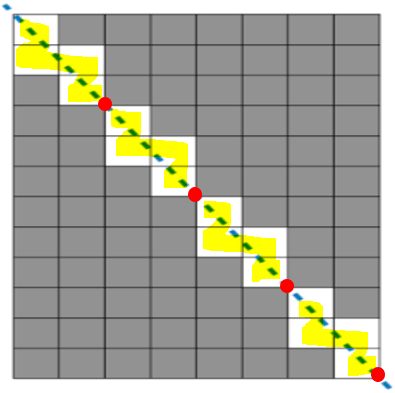
직선이 선이 아닌 교점을 지나는 사각형의 빨간점을 기준으로 비슷한 모양의 패턴이 계속 생겨났다. 이 빨간 점의 갯수는 4로 W:8, H:12의 최대공약수 값과 같았다.
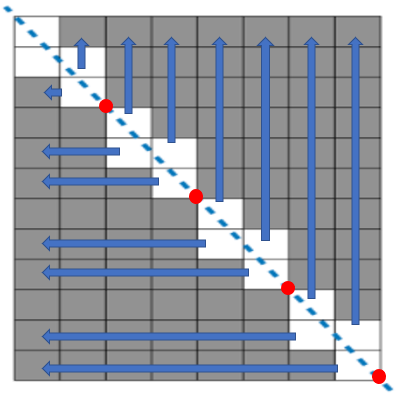
직선이 지나는 사각형들을 가로와 세로 끝으로 보내볼 수 있었다. 그런데, W와 H만큼 다 꽉차는 게 아니라 중간 중간 비어있는 공간이 생겼고 이것이 빨간색 교점과 유사한 위치에서 발견되었다.
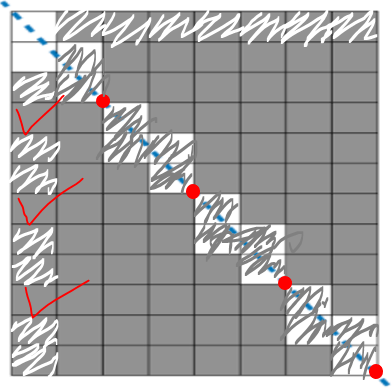
다음과 같은 모양이 되는데 가로, 세로에 안 채워지는 사각형이 3개 있었다. 직선이 지나는 사각형의 갯수를 수식으로 표현하면, W+H - 3 - 1(W와 H 중복으로 세지는 경우) 이었고 결국 빼는 값이 앞에서 유추한 W와 H의 최대공약수 4와 같다는 점을 발견했다.
→ (직선이 만나는 사각형 갯수) = (W + H) - gcd(W,H)
그래서 최대공약수가 1인 경우에도 유추한 규칙의 수식이 성립하는 지 알아보려고 했다. 최대공약수가 1일 때도 1을 빼야하는 이유는 앞에서 보았듯이 W와 H 중복으로 세어지는 경우이므로 위의 수식이 성립했다.
따라서, 전체 수식은 (전체 사각형 갯수)에서 (직선이 만나는 사각형 갯수)를 뺀 (W * H) - ((W + H) - gcd(W,H))이 사용할 수 있는 (멀쩡한 사각형의 갯수)이다.
import math
def solution(w,h):
return w*h - (w+h-math.gcd(w,h))👏다른 사람의 풀이
이 문제는 어떤 알고리즘을 풀이한다기보다는 수학적으로 규칙을 발견하는 문제에 가까운 것 같다.(좋은 문제인지는..잘..)
그래서 다른 사람들의 로직을 이해하는게 어렵기도 하고 도움이 될지는 잘 모르겠다. 그런데 보통 최대공약수를 이용하려고들 많이 한 것 같다.
에서 내가 생각한 것과 비슷하면서 다른 방식으로 잘 설명해주셨다.
🥇 Today I Learn
코딩 테스트 문제를 풀이할 때, 입출력 값의 제한 사항을 보다보면 문제를 어떻게 풀이해야 할지 대략적인 힌트를 얻을 수 있는 것 같다.
위 문제에서는 입력 값이 1억 이하의 자연수 였기 때문에 반복문을 사용한다면 시간복잡도가 상당해질 것으로 예상해서 규칙을 발견하는 것으로 방향을 바꾼 것이 도움이 되었다.