🧐 문제 설명

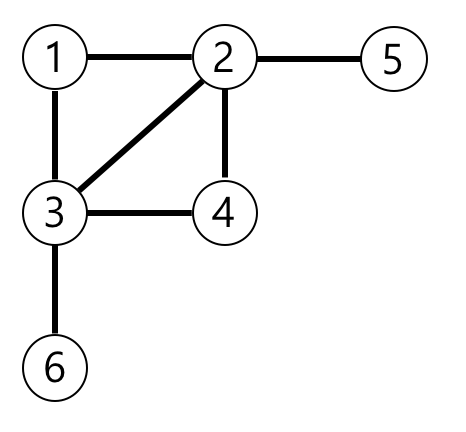
입출력 예 설명
😍 나의 풀이
그래프 문제를 보면 BFS 혹은 DFS가 바로 떠오른다. 이 문제는 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드의 갯수를 구하는 문제이므로 BFS를 선택했다.
1. 그래프 연결 관계 표현하기
주어진 간선(edge) 리스트를 그래프로 표현하는 것이 필요했다. 파이썬에서 그래프는 딕셔너리를 이용해서 쉽게 표현할 수 있으므로 {노드 번호(Key) : 연결 노드(Value)}인 딕셔너리를 만들었다. 무방향성 그래프이므로 예를 들어, [3,2] 간선은 [2,3]을 의미하기도 했다. 그래서 키, 값을 번갈아가며 넣어주었다.
2. BFS 구현하기
최단 경로로 탐색해야하기 때문에 이미 방문한 곳은 다시 방문하지 않도록 방문 처리를 할 수 있는 (노드의 갯수 + 1) 만큼의 visited 리스트를 생성했다.(+1을 한 이유는 노드 번호가 1부터 시작해서 노드 번호와 인덱스를 보기 좋게 일치시키기 위함 ㅎ)
이 후, deque을 이용해 BFS를 구현한다. 초기 값으로 1번 노드를 넣어주고 인접 노드를 체크하여 방문하지 않은 노드이면 덱에 노드를 삽입하고 방문처리한다.
이 과정에서 가장 멀리 있는 노드를 찾아야 하기 때문에 경로의 길이를 count 하기 위해 방문 처리를 1로 하는 것이 아니라 (방문 직전 노드까지의 경로길이 + 1)로 할당했다.
3. 정답
결과적으로 visited 리스트의 i번째 값은 1번 노드에서 출발하여 i번 노드까지의 경로 값이 나온다. 정확하게는 1번 노드가 방문처리 때문에 1로 초기화하고 시작하기 때문에 경로 + 1 값이긴 하다..ㅎㅎ 그래서 가장 먼 노드를 위해 최대값을 찾아서 그 갯수를 count해준다.
from collections import deque
def solution(n, edge):
graph = dict()
visited = [0] * (n+1)
for i in range(1, n+1): # 빈 딕셔너리 생성 {노드 번호: [연결노드]}
graph[i] = []
for i in edge: # 딕셔너리 키 - 값 할당
graph[i[0]].append(i[1])
graph[i[1]].append(i[0])
return bfs(graph, n, visited)
def bfs(graph, n, visited):
queue = deque([1]) # 큐에 시작 노드 1 삽입
visited[1] = 1
while queue:
v = queue.popleft()
for i in graph[v]:
if visited[i] == 0:
visited[i] = visited[v] + 1
queue.append(i)
return visited.count(max(visited))👏 다른 사람의 풀이
그래프 연결 상태를 딕셔너리가 아닌 리스트로 0~n-1까지 인덱스로 1~n번 노드의 연결상태를 표현했다.
또 나는 방문 처리를 위한 visited 리스트만 만들어서 이것만으로 경로의 길이까지 처리했는데 이사람은 경로의 길이만 기록하는 distances 리스트를 따로 만들어서 코드를 안 짠 사람이 봐도 더 가독성이 좋아보인다.
def solution(n, edge):
graph =[ [] for _ in range(n + 1) ]
distances = [ 0 for _ in range(n) ]
is_visit = [False for _ in range(n)]
queue = [0]
is_visit[0] = True
for (a, b) in edge:
graph[a-1].append(b-1)
graph[b-1].append(a-1)
while queue:
i = queue.pop(0)
for j in graph[i]:
if is_visit[j] == False:
is_visit[j] = True
queue.append(j)
distances[j] = distances[i] + 1
distances.sort(reverse=True)
answer = distances.count(distances[0])
return answer
