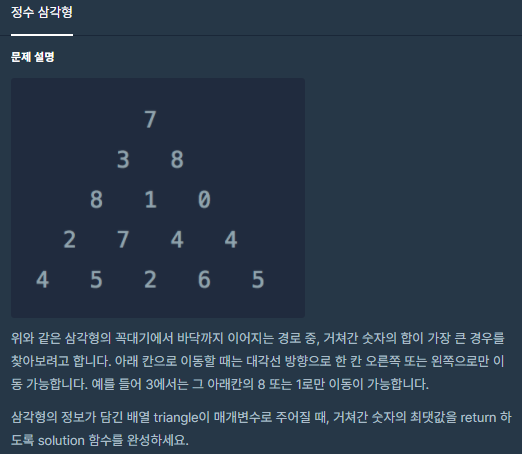
🧐 문제 설명
😍 나의 풀이
DP 문제를 처음 풀려고 하니까 조금 생소했다. DP 문제는 이전의 값들이 현재 값에 영향을 주는 경우가 많다. 그래서 low단계에서부터 하나씩 써보면서 규칙을 발견하면 쉽게 점화식 혹은 규칙을 발견할 수 있다.
이전의 값에서 한 단계 트리를 내려오려면 좌, 우 두 가지 방향으로 진행할 수 있다. 이 과정을 2가지의 경우로 나눌 수 있었다.
1. 왼쪽 끝 혹은 오른쪽 끝으로 진행하는 경우

→ 이 경우는 Max 값을 계속 저장하기 위해서 이전의 값 중 높은 것을 선택하는 고민을 할 필요가 없었다. 왜냐하면 현재 값은 이전에서 올 수 있는 방향이 1가지 뿐이라, 무조건 이전 값에 더한 값이기 때문이다.
2. 그 외 중간으로 진행하는 경우

→ 중간으로 진행한다면 트리의 직전 행에서 좌, 우에서 진행할 수 있다. 문제는 최댓값을 출력해야 하기 때문에 좌, 우에서 올 수 있는 값들 중 큰 값을 현재 값과 더하면 된다.
예시 풀이
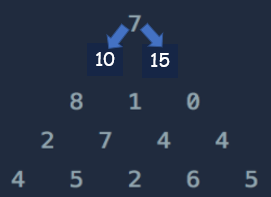
예시와 같은 삼각형이 있을 때, 처음에는 양쪽 끝으로 진행하는 경우밖에 없기 때문에 이전 값을 현재 값에 더한다.

이제 2번째 행에서 3번째 행으로 진행하기 위해서 8과 0은 양쪽 끝이므로 이전 값에서 더하면 된다. 하지만 1의 경우는 10과 15 좌, 우에서 진행되는 값이므로 최댓값을 가지기 위해 둘 중 큰 값인 15를 더해준다.

다음을 마지막 행까지 반복하다가 마지막 행의 가장 최대값을 출력하면 된다.
def solution(triangle):
for i in range(1, len(triangle)):
for j in range(i+1):
if j == 0: # 왼쪽 끝으로 진행
triangle[i][j] += triangle[i-1][j]
elif j == i: # 오른쪽 끝으로 진행
triangle[i][j] += triangle[i-1][j-1]
else: # 그 외 중간으로 진행
triangle[i][j] += max(triangle[i-1][j-1], triangle[i-1][j])
return max(triangle[-1])👏 다른 사람의 풀이
사실 내가 푼 풀이 방식이 DP 인지 잘 모르겠다. 어떻게 보면 Greedy한 것 같기도 하고 탐색 같기도 하고... 처음 풀이해보는 알고리즘이라서 DP가 뭐냐고 명확하게 설명하기가 힘든 것 같다.
이 풀이는 그래도 재귀를 통해 이전의 값이 반복적으로 영향을 주는 것이 분명하게 보이는 DP 코드 인 것 같아서 가져왔다.
def solution(triangle):
memo = {}
answer = f(triangle, 0, 0, memo)
return answer
def f(triangle, i, j, memo):
if i == len(triangle)-1:
return triangle[i][j]
if (i,j) in memo:
return memo[(i,j)]
a = f(triangle, i+1, j, memo)
b = f(triangle, i+1, j+1, memo)
x = triangle[i][j] + max(a, b)
memo[(i,j)] = x
return x🥇 Today I Learn
Dynamic Programming(DP)
DP 조건
1. 최적 부분 구조(Optimal Substructure)
- 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있음
2. 중복되는 부분 문제(Overlapping Subproblem)
- 동일한 작은 문제를 반복적으로 해결해야함
구현 방법(바텀업, 탑다운)
1. Bottom-Up
반복문을 주로 사용하며, 작은 문제에서부터 큰 문제로 나아가며 풀이.
int fibonacci(int n)
{
dp[0] = 0, dp[1] = 1;
for (int i = 2; i <= n; i++)
dp[i] = dp[i - 1] + dp[i - 2];
}2. Top-Down
재귀호출을 주로 사용하며, 큰 문제부터 풀이하며 작은 문제가 풀이되지 않았다면 그때 작은 문제를 해결.
int fibonacci(int n)
{
if (n == 0) return 0;
if (n == 1) return 1;
if (dp[n] != -1) return dp[n];
dp[n] = fibonacci(n - 1) + fibonacci(n - 2);
return dp[n];
}-
Top-down 방식은 점화식을 이해하기 쉽다(가독성이 좋다)는 장점
-
Bottom-up 방식은 함수를 재귀 호출하지 않기 때문에 시간과 메모리 사용량을 줄일 수 있다는 장점

