[BOJ/python] 1260: DFS와 BFS

문제

✔️ silver 2
그래프 이론
그래프 탐색
너비 우선 탐색
깊이 우선 탐색

문제 흐름

방향이 없는 그래프에서 DFS와 BFS 방식으로 각각 탐색한 결과를 출력하면 된다.
이전에 수강한 baaaaarkingdog님의 실전 알고리즘 강의 0x18강-그래프 에서도 나왔듯이 비재귀 방식의 DFS는 이론적으로 생각하는 방문 순서와 다르게 출력된다.
살짝 비효율적으로 작동하게 되지만 비재귀 방식에서도 푸는 방법을 찾고싶어서 고민을 했다.
BFS는 설명할 필요 없이 다른 부분이 없으니 생략하겠다.

💡 비재귀 방식

1. 스택 st에 시작 노드 s를 넣고 방문 확인 딕셔너리 vst에 s를 방문처리 한다. 그리고 탐색 결과를 담을 결과 리스트 res에 s를 넣는다.
2. st에서 한 정점 x를 꺼내 x가 방문하지 않은 정점이라면 방문처리 후 res에 삽입한다.
3. x와 연결된 모든 노드 리스트를 역순으로 정렬(n_lst)한다.
4. n_lst의 각 정점 n에 대해 4번을 진행한다.
5. 방문한 정점이라면 그냥 패스하고, 아니라면 st에 삽입한다.
6. 2번을 st이 빌 때까지 반복한다.

스택에 같은 정점이 여러 번 들어갈 수 있기 때문에 비효율적이고 코드의 직관성도 떨어진다.
재귀방식으로 구현하면 더 간단하게 구현할 수 있다.

💡 재귀 방식

1. res에 현재 입력받은 정점 x를 넣고 방문처리 한다.
2. x와 연결된 모든 정점을 정렬한 리스트 n_lst를 생성한다.
3. n_lst의 각 정점 n에 대해서 방문하지 않았다면 n을 x로 하는 dfs_recursive 함수를 실행시킨다.

코드

# DFS와 BFS 
# graph

import sys
from collections import deque
input = sys.stdin.readline

def bfs(s: int, g: dict):
    q = deque([s])
    vst = {node: 0 for node in range(1, len(g)+1)}
    vst[s] = 1
    res = []
    while q:
        x = q.popleft()
        res.append(x)
        n_lst = sorted(g[x])
        for n in n_lst:
            if vst[n]:
                continue
            q.append(n)
            vst[n] = 1
    return res

def dfs(s: int, g: dict):
    st = [s]
    vst = {node: 0 for node in range(1, len(g)+1)}
    vst[s] = 1
    res = [s]
    while st:
        x = st.pop()
        if not vst[x]:
            vst[x] = 1
            res.append(x)
        n_lst = sorted(g[x], reverse=True)
        # print(f"x={x}: {n_lst}")
        for n in n_lst:
            if vst[n]:
                continue
            st.append(n)
        # print(st)
    return res

def dfs_recursive(x: int, g: dict, vst: dict, res: list):
    res.append(x)
    vst[x] = 1
    n_lst = sorted(g[x])
    for n in n_lst:
        if not vst[n]:
            dfs_recursive(n, g, vst, res)



if __name__ == "__main__":
    n, m, v = map(int, input().split())
    g = {node: [] for node in range(1, n+1)}

    for i in range(m):
        x, y = map(int, input().split())
        g[x].append(y)
        g[y].append(x)

    # res = []
    # vst = {node: 0 for node in range(1, len(g)+1)}
    # dfs_recursive(v, g, vst, res)
    # print( *res )

    print( *dfs(v, g) )
    print( *bfs(v, g) )

마무리

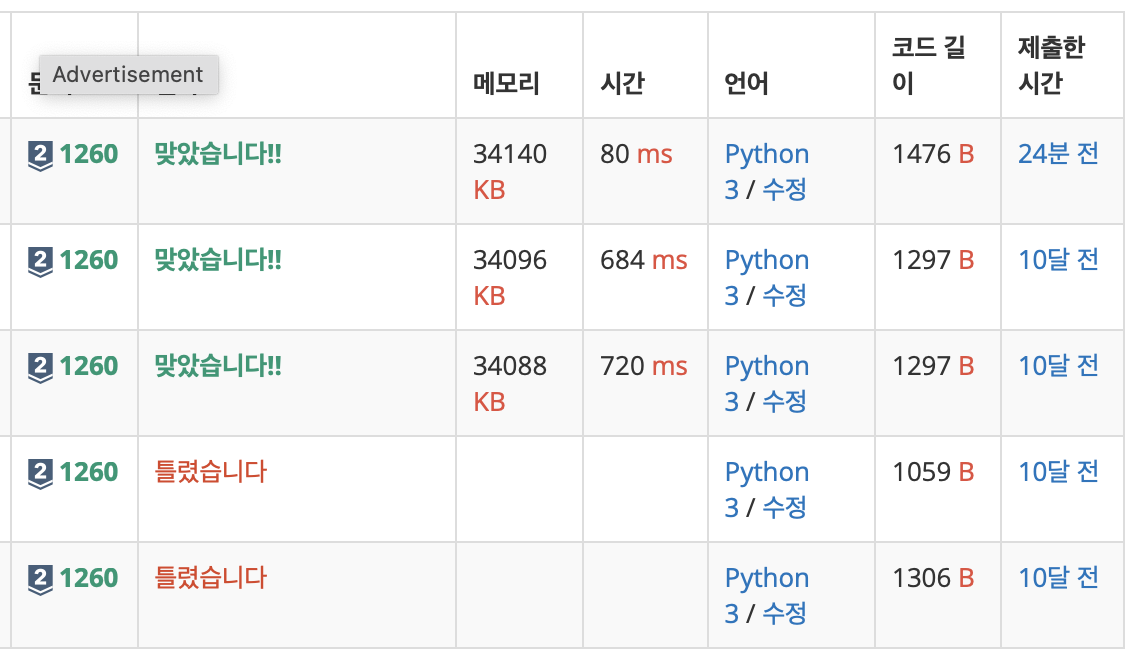
이전 제출 기록이 이번 제출 기록에 비해 시간이 굉장히 오래 걸렸길래 뭐가 문제였을지 살펴봤다.
방문기록을 list에 하나씩 삽입하고 list에 해당 원소가 들어있는가(in) 확인하는 방식으로 진행했던데, 이게 문제였을 것 같다.
과거에 짰던 코드를 보면서 뭐가 문제였었는지 어떻게 생각했었는지 보는 것도 좋은 것 같다.
과거의 나는 정답만 받으면 되는 사람이었군...