
gold 4 / 그리디 알고리즘
문제 흐름
가장 먼저 생각했던 특징은 버튼을 누르는 순서는 상관없다 라는 점이다.
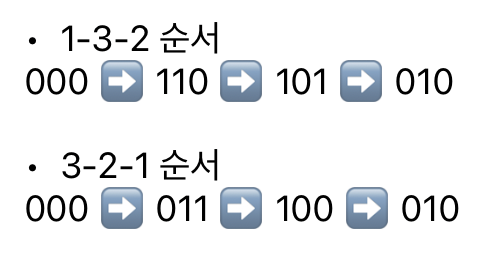
가령 문제에서 제시된 예제 테스트케이스를 생각했을 때, 1-3-2 순서로 스위치를 누르든 3-2-1 순서로 스위치를 누르든 상관이 없다는 얘기다.
하나의 스위치 입장에서 봤을 때 양옆에서 눌리는 수와 본인이 눌리는 수를 카운트하면 순서와는 상관없이 그 합만큼 스위치되기 때문이다.
따라서 0번째 스위치부터 차례로 경우를 확인해도 상관이 없다.
이러한 특징을 고려할 때, 우리는 최소 누르는 수를 구하고자 하기 때문에 눌렀던 스위치를 다시 누르는 것은 의미가 없음을 알게된다.
한 위치의 스위치는 한 번만 확인하게 되는데 이 기준은 무엇이 적합한가?
앞에서부터 차례로 스위치의 상태를 결정한다고 할 때 바로 앞 전구는 현재 스위치가 아니면 더이상 바뀔 기회가 없기 때문에 직전 전구가 target 전구 상태와 다르다면 현재 스위치를 눌러줘야한다.
이렇게 직전 전구의 일치/불일치 상태를 기준으로 현재 스위치 누름 여부를 결정하면 항상 현재 스위치의 선택지는 누른다/안누른다 중 한가지로 결정된다.
이 부분에서 아 이 문제 greedy구나 생각했다.

그렇다면 경우의 수가 한가지인가?
두가지로 선택지가 갈리는 스위치가 있다.
직전 전구가 없는 첫번째 스위치이다.
첫번째 스위치를 누른다와 안누른다의 경우로 두가지 경우를 진행한 뒤 마지막까지 진행했을 때 현재 전구 상태와 target 전구 상태가 일치하지 않는다면 불가능, 일치한다면 스위치를 누른 횟수를 반환하면 되겠다.
두가지 반환값을 가지고 더 적은 횟수를 출력하면 우리가 목표한 바를 이룰 수 있다!
코드
import sys
from copy import deepcopy
input = sys.stdin.readline
# greedy algorithm
def switch(now: list, switch_idx: int):
on_off = lambda x: '0' if x=='1' else '1'
now[switch_idx] = on_off(now[switch_idx])
if switch_idx-1 >= 0:
now[switch_idx-1] = on_off(now[switch_idx-1])
if switch_idx+1 < len(now):
now[switch_idx+1] = on_off(now[switch_idx+1])
return now
def bulb(now, target):
N = len(now)
times = 0
# print(f"now: {now}")
for i in range(1,N):
if now[i-1] != target[i-1]:
switch(now, i)
times += 1
else:
pass
# print(f"now: {now}, target: {target}")
if ''.join(now) == ''.join(target):
return times
else:
return float('inf')
if __name__ == "__main__":
N = int(input())
now = list(input().rstrip())
target = list(input().rstrip())
now1 = deepcopy(now)
res1 = bulb(now1, target) # dont push 1st switch
now2 = deepcopy(now)
res2 = bulb(switch(now2, 0), target) + 1 # push 1st switch
res = min(res1, res2)
if res == float('inf'):
print(-1)
else:
print(res)bulb는 앞서 생각한 버튼 누름 여부를 결정하며 진행하는 함수,
switch는 해당 위치의 스위치를 눌러 전구 상태를 업데이트시키는 함수이다.
마무리
일단 처음에는 재귀를 통해서 모든 경우의 수를 확인해야 한다고 생각했다.
물론 이 경우는 결국 반환값이 두개만 나온다는 점을 생각하지 못한 방법이었다.
불필요하게 여러 경우의 수를 거치다보니 당연히 시간초과를 맞게 됐다.
그리고 이 과정에서 deepcopy도 재귀를 거치며 남용했더니 오랜만에 메모리 초과도 맛볼수있었다.
항상 재귀를 사용하면 시간복잡도를 고려하기 어렵다는 문제가 생긴다..
