DFS와 BFS 알고리즘

문제를 보기 전에 DFS와 BFS 내용을 처음 알아서 먼저 간단히 정리해보려 한다.

두 개념은 대표적인 탐색 알고리즘이다. 탐색 알고리즘이란, 많은 데이터 중에서 원하는 데이터를 찾는 방법을 의미한다. 프로그래밍에서는 주로 그래프와 트리 자료구조 내에서 탐색하는 문제를 자주 다룬다.

DFS (Depth-First Search)

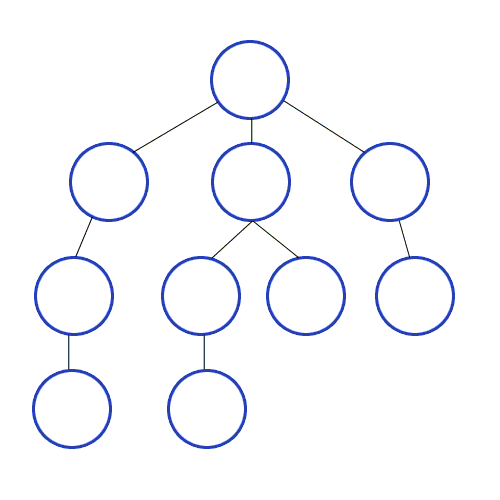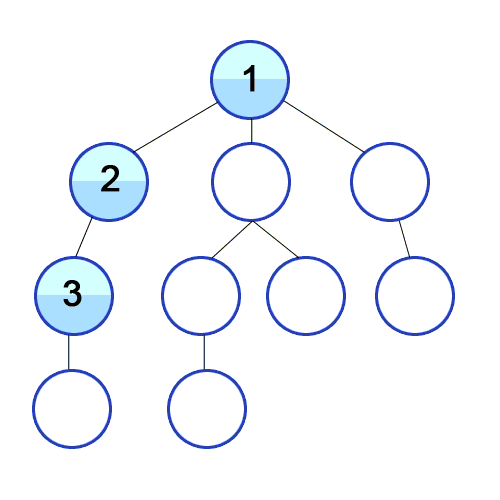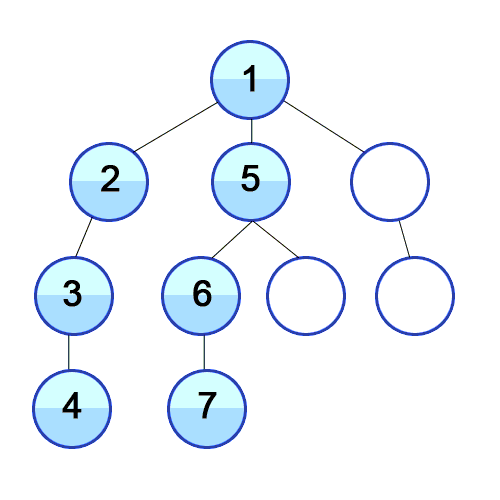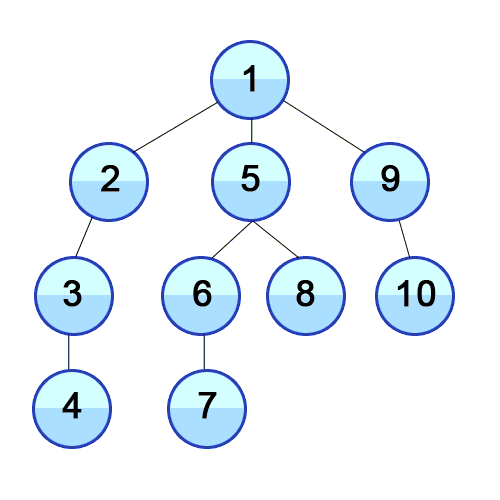
DFS란 깊이 우선 탐색 알고리즘이다. 시작 노드에서부터 한 경로를 따라 최대한 깊게 탐색한 후, 다른 경로를 탐색한다. DFS는 스택 혹은 재귀로 구현되는데, 방문한 노드를 스택에 저장하고, 더이상 탐색할 수 없을 때 스택에서 노드를 꺼내어 역순으로 출력한다.

그래프의 구조를 파악하는 데 유용하며, 미로 찾기 등의 문제를 해결하는데 활용된다.

BFS (Breadth-First Search)

BFS란 너비 우선 탐색 알고리즘이다. 시작 노드에서부터 인접한 노드를 모두 탐색한 후, 다음 노드로 이동한다. BFS는 큐로 구현되는데, 방문한 노드를 큐에 저장하고, 먼저 저장된 노드부터 출력한다.

최단 경로를 찾거나, 노드 간 최단 거리 등을 구하는 데 주로 활용된다.

활용 예시

DFS와 BFS는 조건 내 모든 노드를 방문한다는 점에서 시간 복잡도가 동일하다. 그렇다면 어떤 상황에서 각각을 사용하는지 알아보자.

DFS 활용 예시

1. 미로 또는 퍼즐 풀기(역추적 문제)

• DFS는 해결책을 찾을 때까지 문제의 가능한 모든 경로를 탐색해야 하거나 막다른 골목에 도달했을 때 되돌아가야 할 때 이상적
• 미로 또는 스도쿠 퍼즐을 푸는 경우, DFS는 대안을 시도하기 전에 하나의 경로를 완전히 탐색하여 올바른 솔루션을 찾기 위한 체계적인 접근 방식을 허용

2. 복잡한 그래프의 길찾기

• 큰 그래프에서 노드 간 경로를 검색할 때 솔루션이 반드시 가장 짧을 필요는 없지만 먼저 더 깊은 탐색이 필요한 경우 DFS가 사용되는 경우가 많음
• 체스와 같은 인공 지능 게임에서 DFS는 의사 결정 트리의 심층 검색에 사용될 수 있으며 가능한 이동 순서를 심층적으로 분석하여 장기 전략을 분석할 수 있음

BFS 활용 예시

1. 가중치가 없는 그래프에서 최단 경로 찾기

• BFS는 이웃을 레벨별로 탐색하므로 비가중 그래프에서 최단 경로를 찾아야 할 때 일반적으로 사용
• 내비게이션 시스템(예: Google 지도)에서 BFS는 모든 경로의 가중치가 동일할 때 두 위치 사이의 최단 경로를 찾는 데 도움이 됨

2. 소셜 네트워킹 사이트 (친구 추천)

• BFS는 소셜 네트워크에서 어느 정도 가장 가까운 연결(친구의 친구)을 찾는 데 사용됨
• LinkedIn은 BFS를 사용하여 2차 또는 3차 연결을 식별하여 잠재적인 새 연결로 제안

3. 웹 크롤러

• BFS는 웹 크롤러가 웹을 탐색하고 색인을 생성하는 데 사용
• 크롤러는 웹페이지에서 시작한 다음 다음 레벨로 이동하기 전에 해당 페이지의 모든 링크를 탐색
• 예를 들어, 한 웹페이지에서 다른 웹페이지로 크롤링하여 연결 가능한 모든 링크를 데이터베이스에 추가하는 웹 검색 엔진에 사용

---

📍DFS와 BFS

문제 보러가기

💭 그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.

입력
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.

출력
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.

풀이

개념으로 공부한 DFS와 BFS 알고리즘을 파이썬 코드로 구현해 볼 수 있는 기본 문제이다.

N, M, V = map(int, input().split())

# 그래프 생성
graph = [[0] * (N + 1) for _ in range(N + 1)]

# 간선 정보 입력
for i in range(M):
    a, b = map(int, input().split())
    graph[a][b] = graph[b][a] = 1

# 방문 기록 초기화
visited_bfs = [0] * (N + 1)
visited_dfs = [0] * (N + 1)

# DFS 함수 (스택 사용)
def dfs(V):
    stack = [V]
    while stack:
        node = stack.pop()
        if visited_dfs[node] == 0:
            visited_dfs[node] = 1
            print(node, end=" ")
            for n in range(N, 0, -1):
                if graph[node][n] == 1 and visited_dfs[n] == 0:
                    stack.append(n)

# DFS 함수 (재귀 사용)
def dfs_재귀(V):
    visited_dfs[V] = 1
    print(V, end=" ")
    for i in range(1, N + 1):
        if graph[V][i] == 1 and visited_dfs[i] == 0:
            dfs_재귀(i)

# BFS 함수
def bfs(V):
    queue = [V]
    visited_bfs[V] = 1
    while queue:
        node = queue.pop(0)
        print(node, end=" ")
        for i in range(1, N + 1):
            if graph[node][i] == 1 and visited_bfs[i] == 0:
                queue.append(i)
                visited_bfs[i] = 1

# DFS 실행
dfs(V)
print()

# 방문 기록 초기화 후 BFS 실행
visited_dfs = [0] * (N + 1)
bfs(V)

---