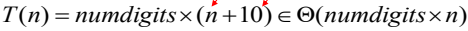Algorithm - sorting - bubble/merge/quick/heap/radix sort

bubble sort

• 인접한 두 원소의 대소를 비교하여 자리를 바꾸어나가면서 정렬한다.
• 구현에 따라 앞에서부터 혹은 뒤에서부터 진행할 수 있다.

pseudo code

python

def bubble_sort(values):
    current = 0
    index = len(values) - 1
    while current < len(values) - 1:
        while index > current:
            if values[index] < values[index - 1]:
                temp = values[index]
                values[index] = values[index - 1]
                values[index - 1] = temp
            index -= 1
        index = len(values) - 1
        current += 1

python 2nd code

def short_bubble(values, numValues):
    current = 0
    sort = False
    while current < numValues - 1 and not sort:
        bubble_up(values, current, numValues - 1, sort)
        current += 1

def bubble_up(values, startIndex, endIndex, sort):
    sort = True
    index = endIndex
    while index > startIndex:
        if values[index] < values[index - 1]:
            temp = values[index]
            values[index] = values[index - 1]
            values[index - 1] = temp
            sort = False
        index -= 1
    return sort

시간복잡도 분석

• 단위연산 : 비교횟수
  
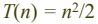
• 단위연산 : 지정문
  

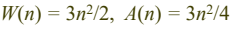
정렬 알고리즘의 비교

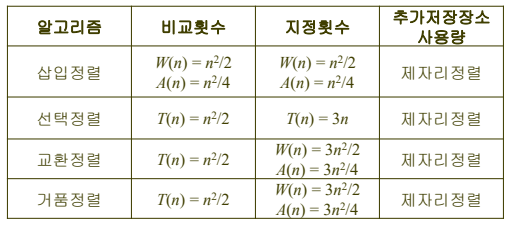
• 삽입정렬은 일정 정도 정렬된 데이터에 대해서 빠르게 수행된다.
• 삽입 정렬은 최소한 교환정렬보다 빠르게 수행된다.
• 일반적으로 선택정렬은 교환정렬보다 빠르다.
• 이미 정렬되어 있는 데이터의 경우에는 선택정렬은 지정이 이루어지지만, 교환정렬은 지정이 이루어지지 않기 때문에 교환정렬이 더 빠르다.
• n의 크기가 크고 키의 크기가 큰 자료구조에서는 지정시간이 많이 걸리기 때문에 선택정렬알고리즘이 삽입정렬 알고리즘보다 빠르다.

merge sort

• 데이터를 반씩 나누어 다루기 쉬운 크기만큼 분할한 후 합병 시에 크기 순으로 합병함으로써 정렬한다.

python

def merge_sort(values, first, last):
    if first < last:
        mid = int((first+last)/2)
        merge_sort(values, first, mid)
        merge_sort(values, mid + 1, last)
        merge(values, first, mid, mid+1, last)

def merge(values, leftFirst, leftLast, rightFirst, rightLast):
    index = leftFirst
    savefirst = leftFirst
    temp = [0] * len(values)
    while leftFirst <= leftLast and rightFirst <= rightLast:
        if values[leftFirst] < values[rightFirst]:
            temp[index] = values[leftFirst]
            leftFirst += 1
        else:
            temp[index] = values[rightFirst]
            rightFirst += 1
        index += 1
    while leftFirst <= leftLast:
        temp[index] = values[leftFirst]
        leftFirst += 1
        index += 1

    while rightFirst <= rightLast:
        temp[index] = values[rightFirst]
        rightFirst += 1
        index += 1

    while savefirst <= rightLast:
        values[savefirst] = temp[savefirst]
        savefirst += 1

분석

• 합병정렬은 한번의 비교마다 하나 이상의 역을 제거하므로 교환/삽입/선택 정렬보다 효율적이다.

Quick sort

• pivot을 설정한 후 데이터를 비교하여 pivot보다 작은 부분과 큰 부분으로 나눔으로써 정렬한다.
• 합병정렬과 다르게 비균등적으로 데이터를 분할한다.

pseudo code

python

def split(values, first, last):
    splitval = values[first]
    savefirst = first
    first += 1
    while True:
        onCollectSide = True
        while onCollectSide:
            if values[first] > splitval:
                onCollectSide = False
            else:
                first += 1
                onCollectSide = (first <= last)
        onCollectSide = (first <= last)
        while onCollectSide:
            if values[last] <= splitval:
                onCollectSide = False
            else:
                last -= 1
                onCollectSide = (first <= last)
        if first < last:
            temp = values[first]
            values[first] = values[last]
            values[last] = temp
            first += 1
            last -= 1
        if first <= last:
            continue
        break
    splitPoint = last
    temp1 = values[savefirst]
    values[savefirst] = values[splitPoint]
    values[splitPoint] = temp1
    return splitPoint
    
def quick_sort(values, first, last):
    if first < last:
        splitPoint = split(values, first, last)
        quick_sort(values, first, splitPoint - 1)
        quick_sort(values, splitPoint + 1, last)
    return values

heap sort

binary tree의 종류

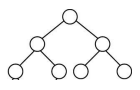
• 완전 이진트리 : 트리 내부에 있는 모든 마디에 2개씩 자식마디가 있는 이진트리
  

• 실질적인 완전이진트리 : 깊이가 d-1까지 완전이진트리이면 깊이가 d인 마디는 왼쪽 끝에서 채워진 이진트리

heap

• 힙의 성질 : 어떤 마디에 저장된 값은 그 마디의 자식마디에 저장된 값보다 크거나 같다(max heap)
• heap : 힙의 성질을 만족하는 실질적인 완전 이진트리
  
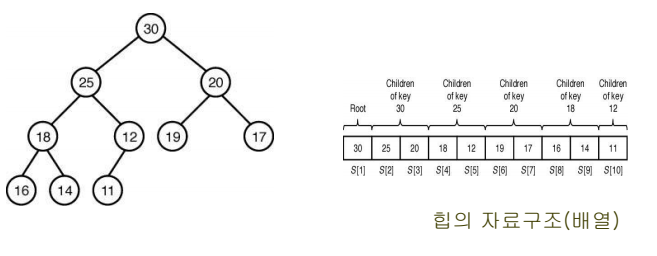
• priority queue를 구현하는데 적합하다.

heap 구조

• index i node의
  - left child index = 2i
  - right child index = 2i + 1
  - parent node index = ceiling(n/2)
  

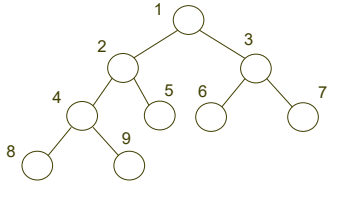
sift down

• 힙성질을 만족하도록 하는 재구성방법
• 요소 삭제로 인한 루트의 키가 힙성질을 만족하지 않을 때 사용한다.
  

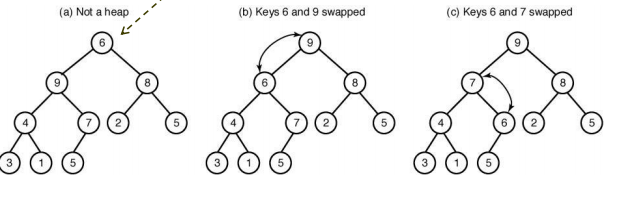
siftdown pseudo code

heap sort pseudo code

heap을 만드는 방법

• 방법 1 : 데이터가 입력되는 순서대로 매번 heap을 구성하는 방법
  

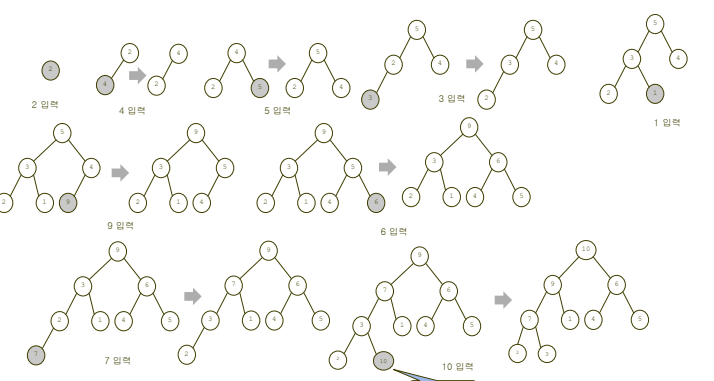
• 시간 복잡도 :

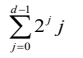
• 방법 2 : 모든 데이터를 입력한 상태에서 heap을 구성하는 방법
  

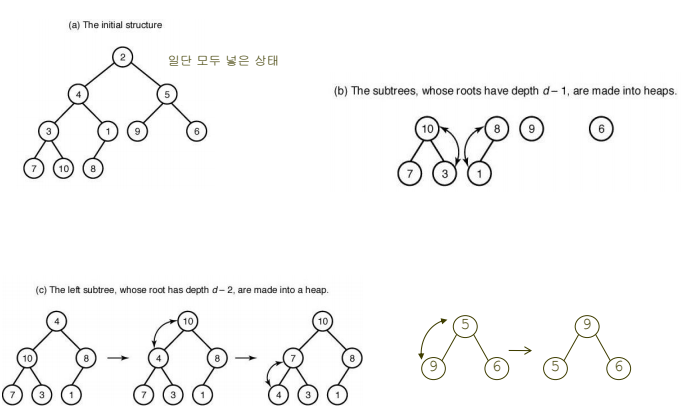
• 시간 복잡도 :

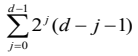
공간복잡도

• 힙정렬은 힙을 배열로 구현한 경우에는 제자지정렬 알고리즘으로써 공간복잡도는 Θ(1)이다.

python

class Heap(object):
    n = 0

    def __init__(self, data):
        self.data = data
        self.n = len(self.data) - 1

    def addElt(self, elt):
        # 요소를 하나 추가하고 heap 형태를 유지하는 함수입니다.
        self.data.append(elt)
        self.n += 1
        self.siftup(self.n)

    def siftup(self, i):
        # 자식 노드가 부모노드보다 크다면 key값을 상호 교환하고
        # i를 i//2로 바꾸어 root까지 진행합니다.
        while i >= 2:
            if self.data[i] > self.data[i//2]:
                temp = self.data[i//2]
                self.data[i//2] = self.data[i]
                self.data[i] = temp
            i = i//2

    def siftdown(self, i):
        siftkey = self.data[i]
        parent = i
        spotfound = False
        while 2 * parent <= self.n and spotfound == False:
            # 자식 노드를 가지고 있는 경우에만 반복문 동작
            if 2 * parent < self.n and self.data[2 * parent] < self.data[2 * parent + 1]:
                # 자식 노드가 2개이면서 오른쪽 자식의 key가 더 큰 경우
                largerchild = 2 * parent + 1
            else:
                # 자식 노드가 1개이거나 왼쪽 자식의 key가 더 큰 경우
                largerchild = 2 * parent
            if siftkey < self.data[largerchild]:
                self.data[parent] = self.data[largerchild]
                parent = largerchild
            else:
                spotfound = True
        self.data[parent] = siftkey

    def makeheap1(self):
        # data를 aliasing 후 self.data를 비우고 요소를 하나씩 추가하며
        # siftup을 통하여 heap의 형태를 유지합니다.
        temp_arr = self.data[:]
        self.data = [0]
        self.n = len(self.data) - 1
        for i in range(1, len(temp_arr)):
            self.data.append(temp_arr[i])
            self.n = len(self.data) - 1
            self.siftup(i)

    def makeheap2(self):
        # self.data길이의 2로 나눈 몫은 항상 자식 노드를 가지는 마지막 node index를 지칭합니다
        # 요소가 모두 추가된 후이므로 자식 노드를 가지는 마지막 노드를 siftdown을 통해
        # sub heap이 heap의 형태를 갖추게 하며 index를 하나씩 줄여가며
        # root node까지 진행합니다.
        for i in range(len(self.data)//2, 0, -1):
            self.siftdown(i)

    def root(self):
        # root의 key값을 저장한 뒤 맨 마지막 배열의 위치와 교환하고
        # 맨 마지막 요소를 삭제합니다
        # 그리고 다시 heap의 형태를 갖춘 후 root의 key값을 반환합니다.
        keyout = self.data[1]
        self.data[1] = self.data[self.n]
        del self.data[self.n]
        self.n -= 1
        if self.n > 0:
            self.siftdown(1)
        return keyout

    def removekeys(self):
        # root의 key를 temp_arr에 저장하고 root값을 제거한 후
        # 다시 heap의 형태로 만들고 root 값이 없을 때 까지 진행합니다.
        temp_arr = []
        for i in range(self.n, 0, -1):
            temp_arr.append(self.root())
        return temp_arr


def heapsort1(a):
    a = Heap(a)
    a.makeheap1()
    ans = a.removekeys()
    return ans


def heapsort2(a):
    a = Heap(a)
    a.makeheap2()
    ans = a.removekeys()
    return ans


if __name__ == '__main__':
    a = [0, 11, 14, 2, 7, 6, 3, 9, 5]
    b = Heap(a)
    b.makeheap1()
    print("방법 1의 makeheap 후 data : ", b.data)
    s = heapsort1(a)
    print("heap sort 후의 data : ", s)
    print()

    c = Heap(a)
    c.makeheap2()
    print("방법 2의 makeheap 후 data : ", c.data)
    c.addElt(50)
    print("방법 2의 50 추가 후 data : ", c.data)
    s2 = heapsort2(a)
    print("heap sort 후의 data : ", s2)

기수정렬

• 자리수에 따라 분류함으로써 정렬하는 방법

pseudo code

시간복잡도 분석