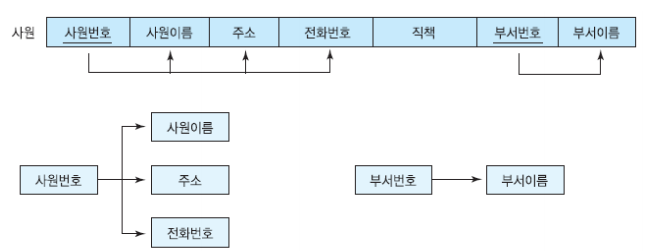
결정자
- 어떤 attribute의 값을 다른 attribute의 값을 고유하게 결정할 수 있다.
- 다른 attribute를 고유하게 결정하는 하나 이상의 attribute를 의미한다.
- A가 B를 결정한다 / A는 B의 결정자이다 / A → B
함수적 종속성 (제 2정규형 ~ BCNF까지 적용된다)
- attribute A가 attribute B의 결정자이면 B가 A에 함수적으로 종속한다
- attribute B가 attribute A에 함수적으로 종속하는 필요 충분 조건은 각 A값에 대해 반드시 한 개의 B값이 대응되는 것이다.
- 정규화 이론의 핵심
- 릴레이션의 attribute들의 의미로부터 결정된다.
- 스키마에 대한 주장이며, 특정 인스턴스에 대한 주장이 아니다.
- 릴레이션의 가능한 모든 인스턴스들이 만족해야 한다.
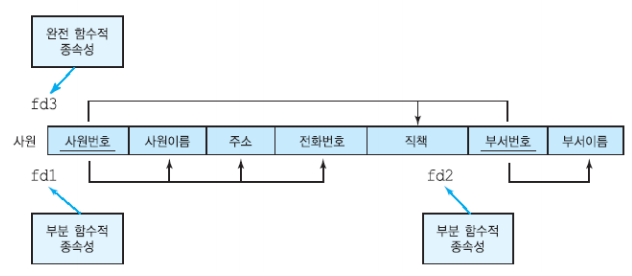
완전 함수적 종속성(FFD, Full Functional Dependency)
- 주어진 릴레이션에서 attribute B가 attribute A에 함수적으로 종속하면서 attribute A의 어떠한 진부분 집합에도 함수적으로 종속하지 않으면 완전하게 함수적으로 종속한다.
이행적 함수적 종속성
- 한 릴레이션의 attribute A, B, C가 주어졌을 때 attribute C가 이행적으로 A에 종속한다는 것의 필요 충분 조건은 A→B ∧ B → C 가 성립하는 것
- A가 릴레이션의 기본 키라면 키의 정의에 따라 A→B와 A→C가 성립한다
- 만약 C가 A 외에 B에도 함수적으로 종속한다면 C는 A에 직접 함수적으로 종속하면서 B를 거쳐서 A에 이행적으로 종속한다고 표현한다.
릴레이션 분해
- 하나의 릴레이션을 두 개 이상의 릴레이션으로 나누는 것
- 중복이 감소되고, 갱신 이상이 줄어들지만 몇가지 문제를 야기할 수 있다
분해되기 전에는 조인이 필요 없는 질의가 분해 후에는 조인을 필요로 할 수 있다.
분해된 릴레이션들을 사용하여 원래 릴레이션으로 재구성하지 못할 수 있다.
무손실 분해
- 분해된 두 릴레이션을 조인하면 원래의 릴레이션에 들어 있는 정보를 완전하게 얻을 수 있다.
- 손실은 정보의 손실을 뜻하며 원래의 정보보다 많거나 적은 경우 모두를 뜻한다.
부분 함수적 종속성이 발생하기 위한 조건
- 기본키가 2개 이상의 attribute
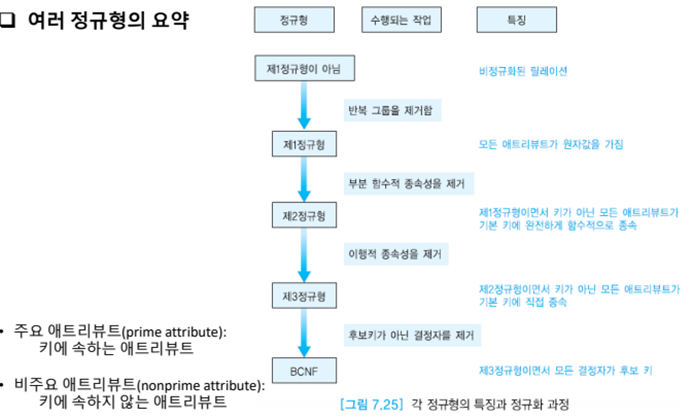
제 1정규형
- 제 1정규형을 만족할 필요 충분 조건은 모든 attribute가 원자값만을 갖는다는 것이다.
- 모든 attribute에 반복 그룹이 나타나지 않으면 제 1정규형을 만족한다.
제 1정규형을 만족하지 않은 릴레이션을 제 1정규형으로 변환하는 방법
- 반복 그룹 attribute에 나타나는 집합에 속한 각 값마다 하나의 투플로 표현한다
- 불필요한 중복 데이터가 생성된다.
- 모든 반복 그룹 attribute들을 분리해서 새로운 릴레이션에 넣고, 원 릴레이션의 기본키를 새로운 릴레이션의 후보키로 추가한다.
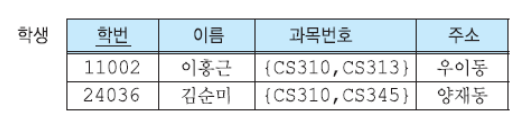
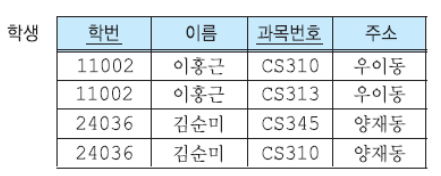
제 1정규형에 존재하는 갱신이상
갱신이상이 생기는 이유 : 기본 키에 대한 부분 함수적 종속성이 존재하기 때문
- 수정 이상
- 중복된 데이터를 저장하고 있는 투플 중에서 일부만 수정되었을 때 데이터 불일치 발생
- 한 학과에 여러 학생이 소속된 경우 소속 학과의 전화 번호가 변경되었을 때 모든 학생이 가지고 있는 전화 번호를 수정해야 한다.
- 삽입 이상
- 엔티티 무결성 제약 조건에 따라 기본키에 널값을 입력할 수 없기 때문에 기본 키 값을 가지지 않는 투플을 삽입할 수 없다
- 한 명의 학생도 소속되지 않은 학과에 대해서는 투플을 삽입할 수 없게 된다.
- 삭제 이상
- 특정 attribute 값의 마지막 값을 가지고 있는 투플을 삭제시 관련된 모든 데이터가 삭제된다.
- 어떤 학과에 소속된 마지막 학생 투플을 삭제하면 이 학생이 소속된 학과에 관한 정보도 삭제된다.
제 2정규형
- 릴레이션이 제 1정규형을 만족하면서, 어떤 후보 키에도 속하지 않는 모든 attribute들이 릴레이션의 기본키에 완전하게 함수적으로 종속하는 것 (부분 함수적 종속성 제거)
제 2정규형에 존재하는 갱신이상
- 갱신 이상이 생기는 이유 : 릴레이션에 이행적 종속성이 생기기 때문
- 갱신이상 : 제 1정규형과 동일한 문제가 발생한다.
수정 방법 : 기본 키가 아니면서 결정자의 역할을 하는 attribute를 새로운 릴레이션으로 분해한다.
- 새로 만든 릴레이션의 기본 키를 기존의 릴레이션의 외래키로 포함시킨다.
제 3정규형
- 제 2정규형을 만족하면서 키가 아닌 모든 attribute는 릴레이션의 기본키에 이행적으로 종속하지 않는 것
- 갱신 이상이 생기는 이유 : 키가 아닌 attribute가 다른 attribute를 결정하기 때문
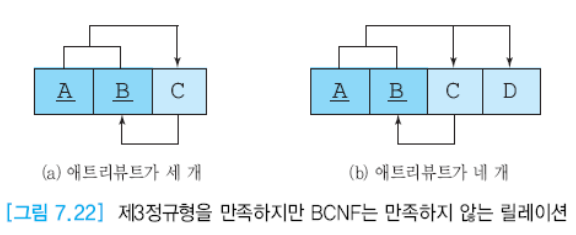
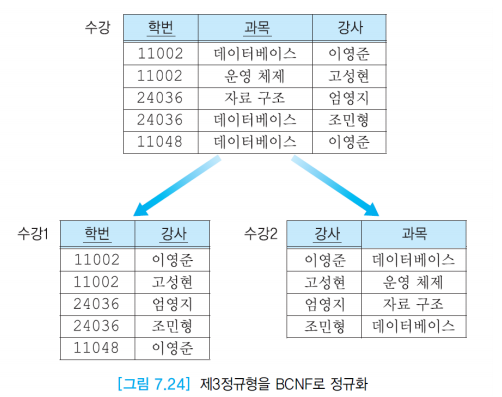
BCNF
- 릴레이션이 제 3정규형을 만족하고 모든 결정자가 후보키이어야 한다.
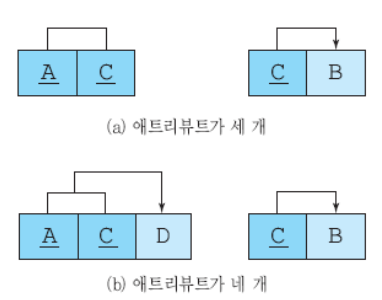
BCNF 만드는 방법
- 키가 아니면서 결정자 역할을 하는 attribute와 그 결정자에 함수적으로 종속하는 attribute를 하나의 테이블에 넣고, 결정자를 기본키로 만든다.
- 기존 릴레이션에 결정자를 남겨서 기본 키의 구성요소가 되도록 한다.
정규화 장점
- 정규화 단계가 진행될수록 중복이 감소하고 갱신 이상도 감소한다.
- 정규화가 진전될수록 무결성 제약조건을 시행하기 위해 필요한 코드의 양도 감소한다.
정규화 단점
- 정규화가 데이터 베이스 설계의 중요한 요소이지만, 성능상의 관점에서만 보면 높은 정규형을 만족하는 릴레이션 스키마가 최적인 것은 아니다.
- 한 정규형에서 다음 정규형으로 진행될 때마다 하나의 릴레이션이 최소 2개의 릴레이션으로 분해된다.
- 분해되기 전의 릴레이션을 대상으로 질의를 할 때는 조인이 필요 없지만, 분해된 릴레이션을 대상으로 질의를 할 때는 같은 정보를 얻기 위해서 보다 많은 릴레이션들을 접근해야 하므로 조인의 필요성이 증가한다. (조인은 계산 비용이 큰 연산자이다)
역정규화
- 데이터 중복 및 갱신 이상을 대가로 성능상의 요구를 만족시키기 위해 사용한다.
- 일반적으로 갱신 질의보다 검색 질의의 비율이 높으며, 역정규화는 주어진 응용에서 빈번하게 수행되는 검색 질의들의 수행 속도를 높이기 위해 두 개 이상의 릴레이션들을 합쳐서 하나의 릴레이션으로 만드는 작업
낮은 정규형으로 돌아가는 작업
FD Closure
- 집합 F하에서 속성 집합 X의 Closure / X+
- 정규화를 위해서 릴레이션을 분해하기 위해서는 FD를 알아야 하고, 원래의 릴레이션에 있던 FD를 이용한 Closure를 통하여 분해될 릴레이션의 FD를 구한다.
- 함수적 종속성 집합 F를 사용하여 X에 의해 함수적으로 결정되는 모든 attribute들의 집합
- X가 결정할 수 있는 모든 애트리뷰트의 집합
- 폐포를 구한 다음 분해된 릴레이션에 대한 FD집합으로 Projection한다.
Projection
- 분해된 릴레이션의 attribute들로만 구성된 FD를 추출하는 것
- 릴레이션을 분해하기 위해서는 FD를 알아야 하므로 Closure를 통하여 폐포를 구한 후 proejection을 통하여 FD를 산출한다.

릴레이션 분해 시 고려 사항
- 무손실 분해
- FD preservation (BCNF로 전환하면서 사라질 수 있다. FD를 보존해야 한다)
