SVD vs MF
MF의 경우 일반적인 data에 적용이 가능하고, sparse한 상황에서도 가능함
FM에서의 wi,j는 공유되지만 SVD에서는 서로 다 독립임
MF에서 dimension의 크기가 클수록 표현력이 좋아지는 것은 맞지만, 학습 데이터의 양이 부족해서 애초에 모든 시그널들을 표현해낼 수가 없다. 따라서 큰 값은 사용하지 않는다.
읽기 전에 드는 의문
-
Rating matrix를 분해하는게 아닌데 어떤 이유로 factorize라는 표현이 들어갔는가?
=> 단순히 가중치가 곱해진 변수들로 평점을 예측하는 model을 만들게 되면 변수들 간의 interaction 표현이 안됨. 따라서 서로 interaction을 반영하도록 만들었고, 그래서 factorize라는 표현을 쓰는듯??
=> SVM의 경우, N개의 feature가 있다면 weight들도 단순히 N개임. FM의 경우, weight를 decompose해서 일종의 latent factor의 조합이라고 볼 수 있겠다!
-
왜 SVM은 sparse data에서 fail하는가?
=> abstract에서 SVM은 fail했다는 표현이 있는데, 일반적으로 SVM은 sparse data에 적합한 것으로 여겨지는듯, 이 논문에서는 collaborative filtering과 같은 very sparse data에서는 reliable하지 않다고 표현함.
-
Sequential Recommender가 아닌데 last movie rated 정보가 필요할까?
재밌는 거 보고 재미 없는 거 보면 평점을 낮게 주나??????Kernel Trick
선형적으로 분리할 수 없는 형태의 데이터 X가 있을 때,
X -> Z라는 고차원으로 옮기면 선형적으로 분리가 될 수 있다. 하지만 차원이 커지면 내적(SVM에 필요함)연산량이 지나치케 커진다.
이때 Z에서 행해지는 내적값을 X 차원에서 원래 데이터 내적 값으로 표현할 수 있도록 하는게 Kernel Trick이다!Abstract
-
FM의 경우 linear time에 계산 가능
-
다른 factorization model들에 비해 general prediction task에 적용 가능하다.
Introduction
SVM의 경우 support vector가 training data의 일부라서 그를 저장해야하는 단점이 있지만, FM의 경우 그럴 필요가 없다.
Factorization mahcines (FM)

단순히 Wij를 쓴 게 아니라 <vi, vj>로 factorizing을 했기 때문에 sparse한 데이터에서도 higher-order interaction 표현이 가능하다.
학습 data가 충분하지 않기 때문에, 제한된 k를 쓰고 이는 일밚놔에 유리해진다.
factorizing을 했기 때문에 하나의 interaction에 대한 data가 관련된 interaction estimate에 모두 영향을 준다.
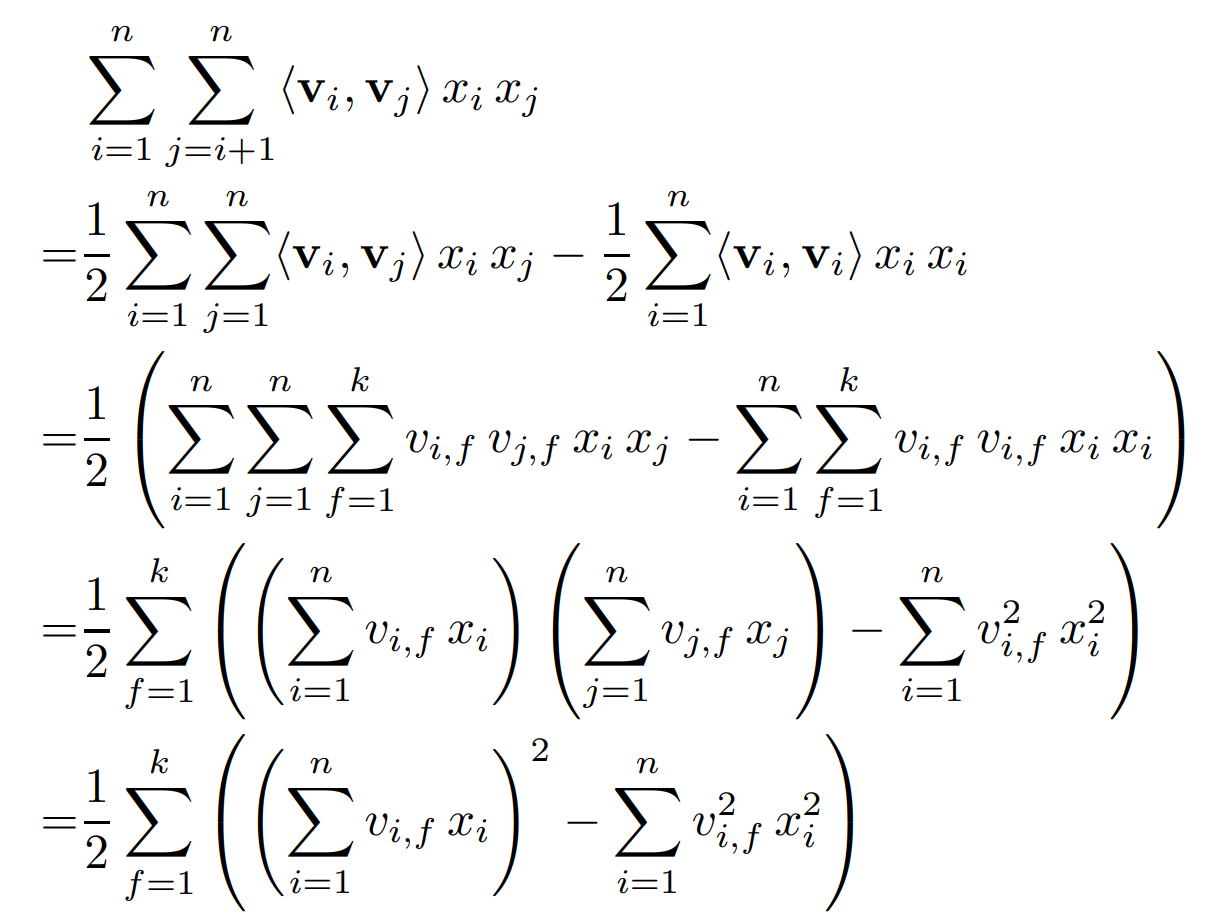
이런 reformulate 과정을 통해 Time complexity가 O(n^2k) -> O(kn)이 됨
Implementation
n에 대해 돌리지말고 웬만하면 m(x)에 대해 돌리기
SGD로 update
와 이걸 뒤에서 설명하네...
SVM VS FM
wi,j는 wi,l에 대해 완전히 독립적 (SVM)
<vi, vj> <vi, vl>은 vi를 공유하기 때문에 서로 의존적(FM)
확실히 이렇게 하면 연산도 단순히 하나-하나 곱하는 거니까,, 빠르고 interaction도 반영이 가능할듯 단순한 아이디어지만 reasonable함,,