재귀적인 해결 방법은 powerful 하고 빈번하게 사용되는 문제 해결 기술이다.
트리는 노드를 값과 자식 노드를 포함하여 재귀적으로 정의하고 있다. 재귀는 트리의 본래 특징 중 하나이다.

그러므로
많은 트리 문제는 재귀적으로 해결할 수 있다.

일반적으로 하향식(Top-down) 또는 상향식(Bottom up) 접근 방법을 사용하여 트리 문제를 반복적으로 해결할 수 있다.

Top down solution

하향식은 각 재귀 호출에서 먼저 노드를 방문하여 일부 값을 생성하고, 함수를 재귀 호출 할 때 이 값을 하위 노드에게 전달하는 것을 의미한다.

하향식 해결법은 일종의 전위(preorder) 순회로 생각할 수 있다.

하향식의 동작 순서는 아래와 같다.

1. return specific value for null node
2. update the answer if needed // answer <-- params
3. left_ans = top_down(root.left, left_params) // left_params <-- root.val, params
4. right_ans = top_down(root.right, right_params) // right_params <-- root.val, params
5. return the answer if needed // answer <-- left_ans, right_ans

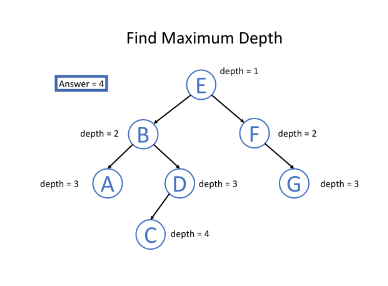
대표적인 예시로, 트리의 최대 깊이를 찾을 수 있다.

1. return if root is null
2. if root is a leaf node:

3. answer = max(answer, depth)         // update the answer if needed

4. maximum_depth(root.left, depth + 1) // call the function recursively for left child
5. maximum_depth(root.right, depth + 1) // call the function recursively for right child

int answer; // don't forget to initialize answer before call maximum_depth
void maximum_depth(TreeNode* root, int depth) {
    if (!root) {
        return;
    }
    if (!root->left && !root->right) {
        answer = max(answer, depth);
    }
    maximum_depth(root->left, depth + 1);
    maximum_depth(root->right, depth + 1);
}

Bottom up solution

상향식은 또 다른 재귀적 문제 해결 방법이다. 각 재귀 호출에서 먼저 모든 자식 노드에 대해 함수를 재귀적으로 호출한 다음 반환된 값과 현재 노드 자체의 값에 따라 답을 도출한다. 이 과정은 일종의 후위(postorder) 순회와 비슷하다.

동작 순서는 아래와 같다.

1. return specific value for null node
2. left_ans = bottom_up(root.left) // call function recursively for left child
3. right_ans = bottom_up(root.right) // call function recursively for right child
4. return answers // answer <-- left_ans, right_ans, root.val

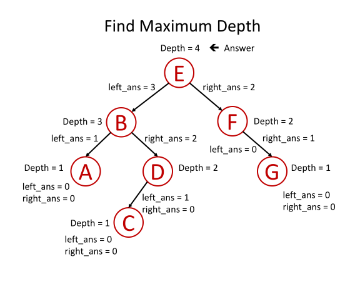
최대 깊이 탐색 코드 순서

1. return 0 if root is null // return 0 for null node
2. left_depth = maximum_depth(root.left)
3. right_depth = maximum_depth(root.right)
4. return max(left_depth, right_depth) + 1 // return depth of the subtree rooted at root

int maximum_depth(TreeNode* root) {
    if (!root) {
        return 0;                                 // return 0 for null node
    }
    int left_depth = maximum_depth(root->left);
    int right_depth = maximum_depth(root->right);
    return max(left_depth, right_depth) + 1;      // return depth of the subtree rooted at root
}