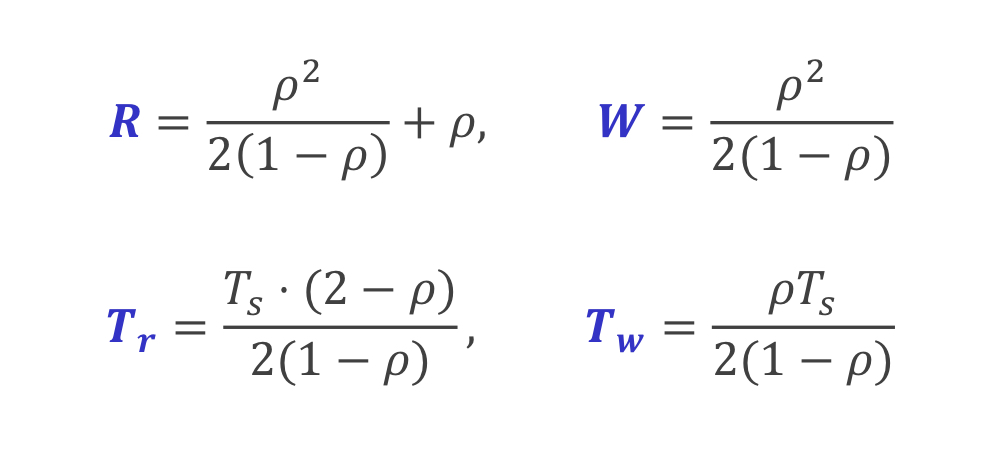Performance in Statistical TDM
Statistical TDM에서의 성능을 살펴봅니다.
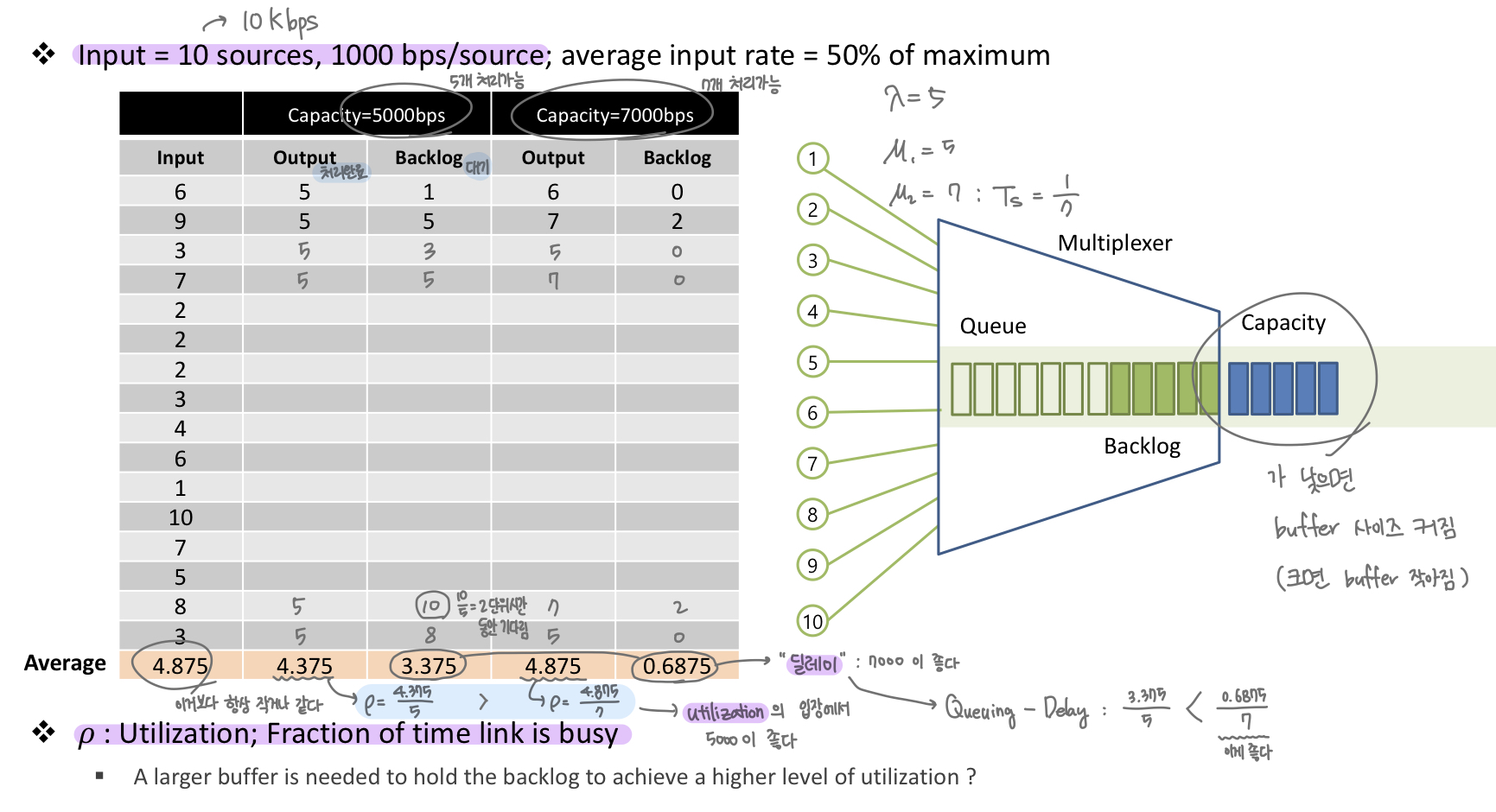
이런식으로, 입력이 계속해서 들어오고 처리용량만큼 처리 후 처리하지 못한 입력은 큐에 남아있어서 다음 클럭에 처리하게 됩니다.
Utilization
링크가 바쁜 정도를 나타낸 수치 입니다. 평균처리용량 / 최대처리용량 으로 나타냅니다. 위 예시를 보면,
- 첫번째 MUX
- 처리 용량은 5Kbps 입니다.
- 평균 출력 용량은 4.375 입니다.
- Utilization 값은 4.375 / 5 입니다.
- 두번째 MUX
- 처리 용량은 7Kbps 입니다.
- 평균 출력 용량은 4.875 입니다.
- Utilization 값은 4.875 / 7 입니다.
Utilization 입장에서는, 첫번째 MUX가 가동률이 더 좋으므로 첫번째가 더 좋다고 할 수 있습니다. 반면, 딜레이를 살펴보면
- 첫번째 MUX : 3.375 / 5
- 두번째 MUX : 0.6875 / 7
이므로 딜레이의 관점에서 보면, 두번째 MUX가 더 좋습니다. 이렇게 성능에 대한 판별은 기준에 따라 달라지기 때문에 ‘성능 개선을 위해’ 라는 의미는 매우 모호한 표현이라고 할 수 있습니다.
Performance in Queueing Models
Queueing model은 다음과 같은 모습입니다.
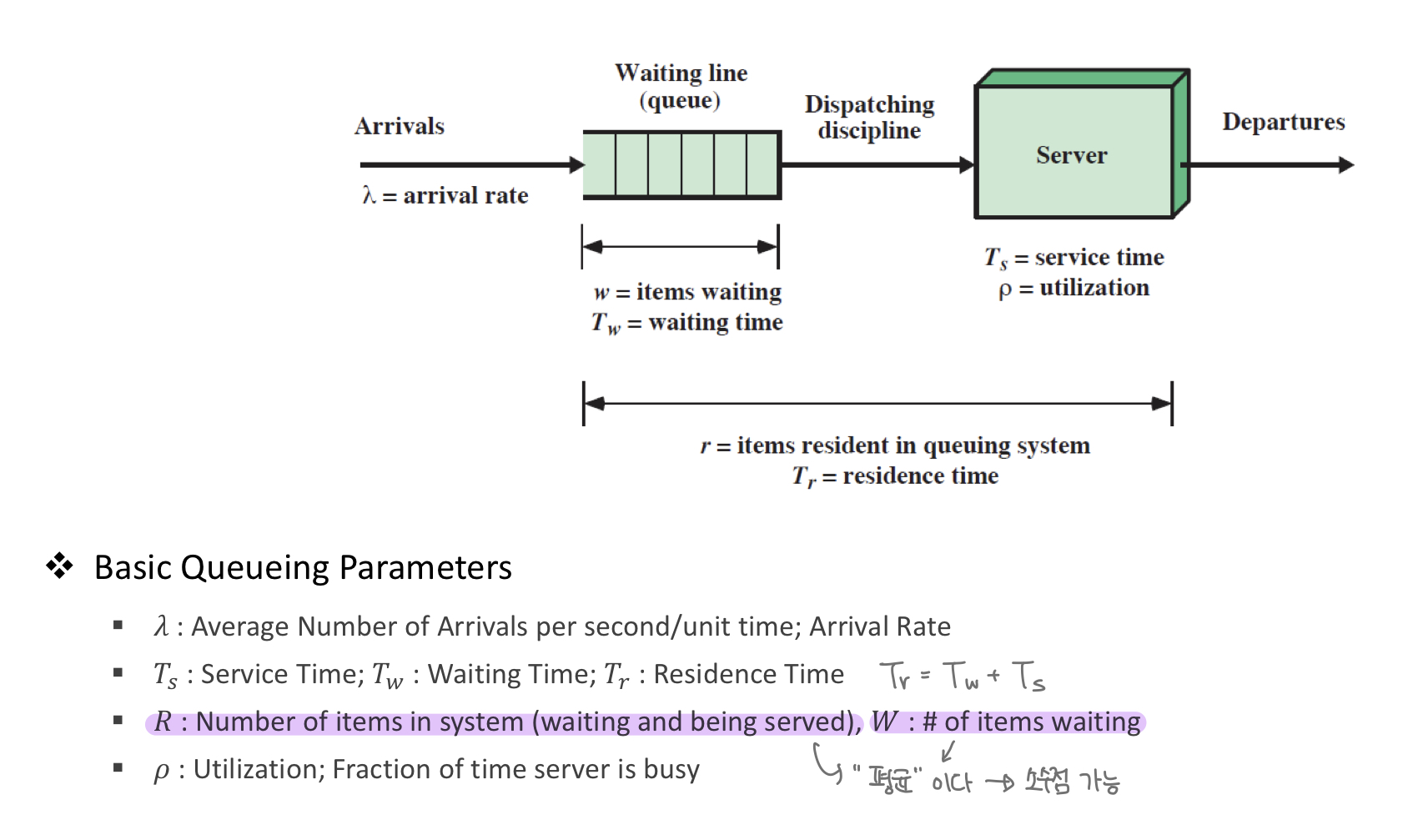
Queueing model에서 성능을 살펴봅시다. 우선 Input Rate - 𝝀 / Output Data Rate - 𝝁 두가지가 등장합니다. 우선, 평균 입력 속도는 출력 속도보다 작아야 합니다. 아니라면?! 큐가 무한정으로 커집니다. 따라서 입력 < 출력 의 관계는 항상 성립해야 합니다. 하지만, 순간적으로 입력이 출력보다 클 수는 있습니다. 이 때를 peak period 라고 합니다.
그리고 큐를 버퍼라고 부릅니다. 𝝁 가 크면 버퍼는 줄어듭니다. 그럼 여기서, 딜레이를 줄이기 위해서 버퍼의 크기를 줄인다 ?? 는 틀렸습니다. Service drop 이 발생할 수 있습니다. 그리고 서버 증설보다 버퍼 증가가 더 비싼 경우도 있습니다.
Queueing Relationships

이런 관계가 성립합니다 !! 그리고 Queueing Model 에서 입력/출력/서버개수 간의 관계를 나타내는 Kendal's Notation 이 있습니다.

Exponential Service (M/M/1)
입력이 exponential, 출력도 exponential 형태이면서 서버의 개수가 1개인 경우입니다.
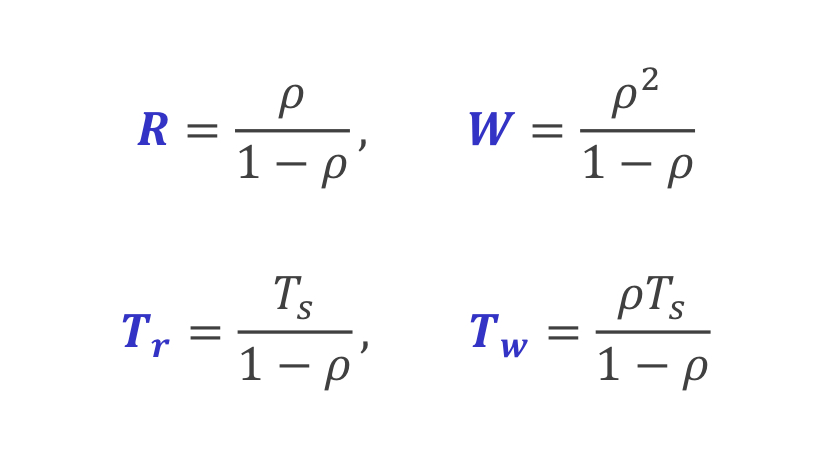
Constant Service Time (M/D/1)
입력은 expoenetial 이면서 출력은 constant 이고 서버의 개수가 1개인 경우입니다.