시간복잡도
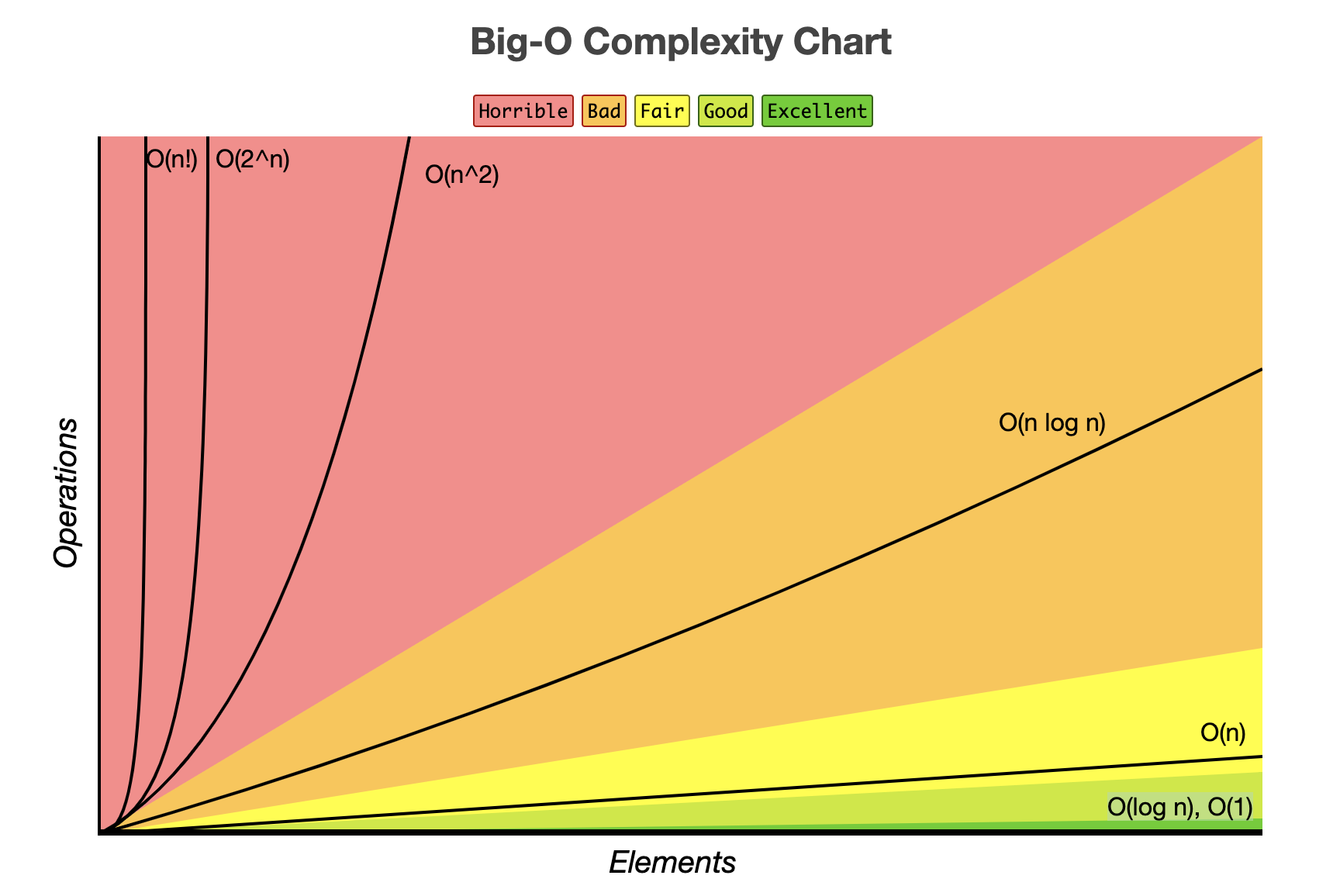
시간복잡도를 고려한다는 것은
'입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?"라는 의미이다.
효율적인 알고리즘은 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 구성했다는 의미이며 시간복잡도는 3개의 표기법이 존재한다.
- Big-O(빅-오)
- Big-Ω(빅-오메가)
- Big-θ(빅-세타)
위 세 가지 표기법은 각각 최악, 최선, 중간의 경우에 대해서 나타내는 방법들이다.
이 중에서도 Big-O 표기법이 가장 많이 사용되는데 그 이유는 다음과 같다.
- Big-O는 최악의 경우를 고려하므로 프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려할 수 있기 때문이다.
- 즉, "최소한 특정 시간 이상이 걸린다" 혹은 "이 정도 시간이 걸린다" 보다는 "이 정도 시간이 걸릴 수 있다"를 고려해야 그에 맞는 대응이 가능하다
최선의 경우 혹은 평균값을 기대하는 시간 복잡도로 알고리즘을 구현한다면, 최악의 경우 어디에서 문제가 발생했는지 알아내기 위해 로직의 많은 부분을 파악해야 하므로 문제를 파악하는데 많은 시간이 필요하다.
그래서, 최악의 경우도 고려하여 대비하는 것이 바람직하기 때문에, 다른 표기법보다 Big-O를 많이 사용한다.
O(1) : 상수
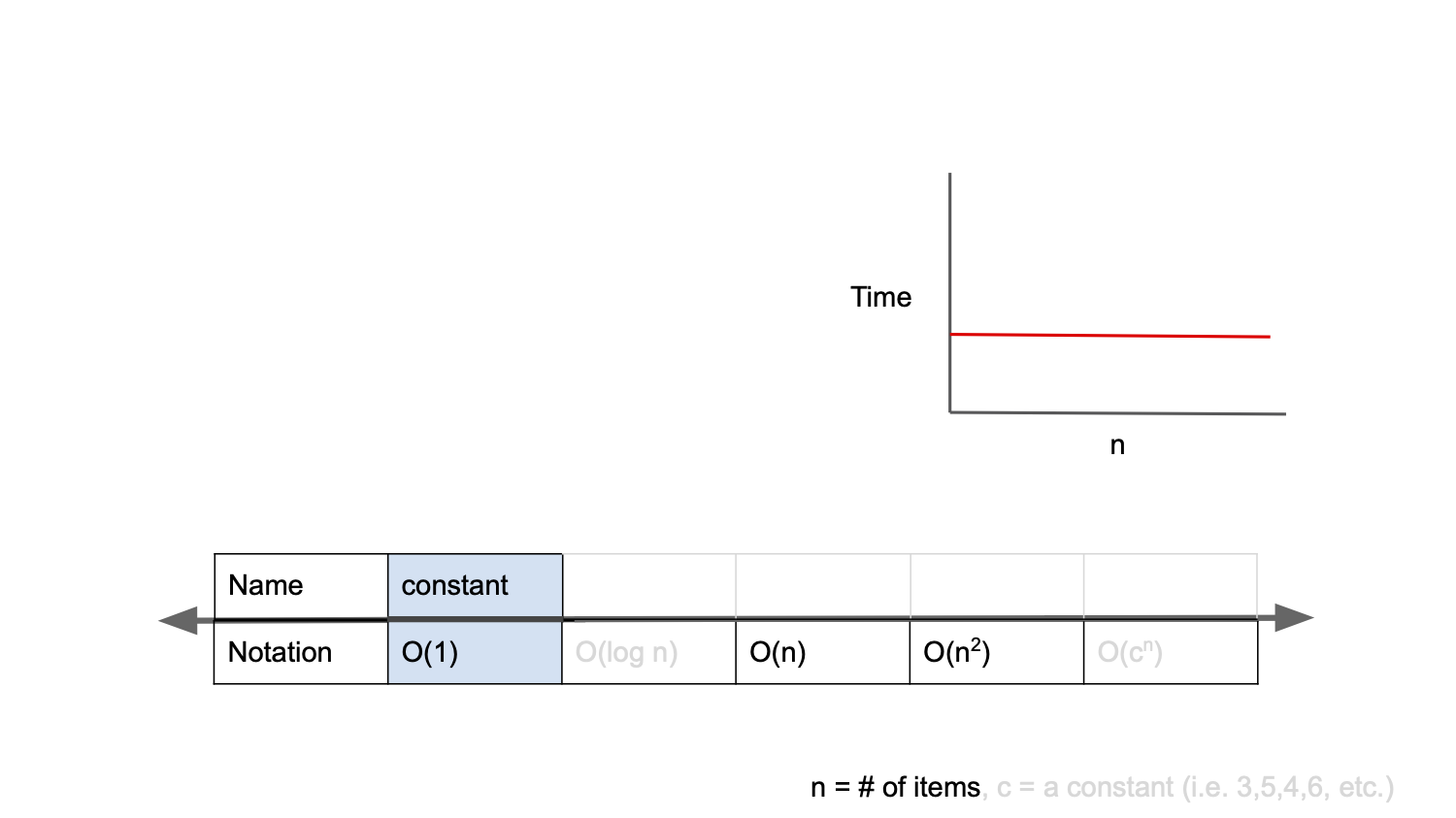
Big-O 표기법의 경우 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼만큼 걸리는가?를 표기하는 방법이다.
O(1)는 constant complexity라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않는다.
즉, 입력값의 크기와 관계없이, 즉시 출력값을 얻어낼 수 있다는 의미이다.
public int O_1_algorithm(int[] arr, int index) {
reutrn arr[index];
}
int[] arr = new int[]{1,2,3,4,5};
int index = 1;
int results = O_1_algorithm(arr, index);
System.out.pritnln(results); // 2- 위 예제처럼 입력의 관계없이 복잡도는 동일하게 유지되며
arr의 크기가 변동되더라도, 즉시 index에 접근하여 값을 반환한다.
O(n) : for문
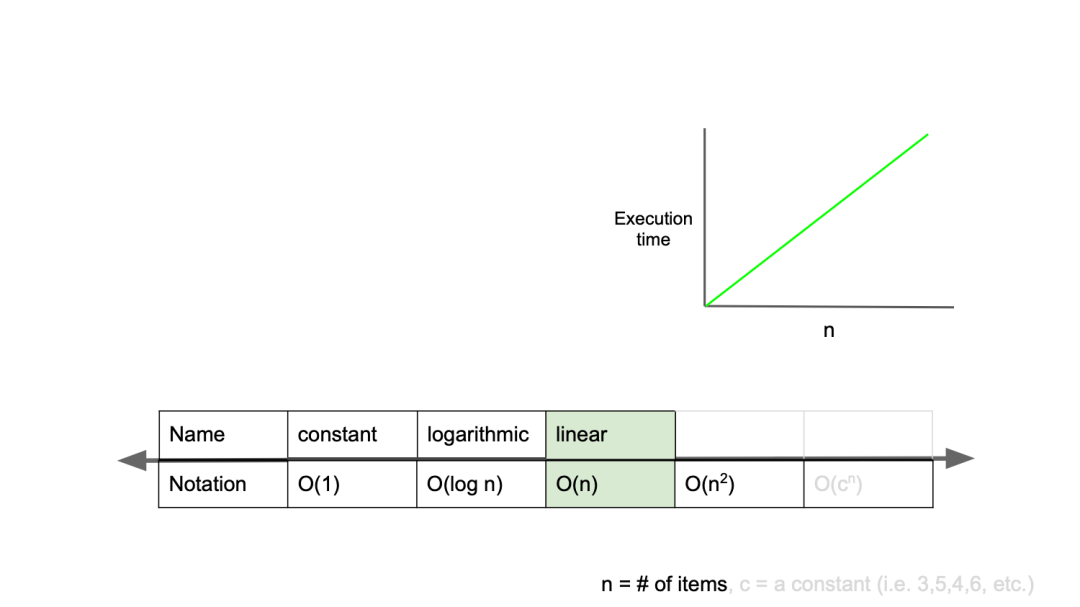
O(n)은 선형 복잡도(linear complexity)라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다.
public int O_n_algorithmn(int n) {
for (int i = 0; i < n; i++){
// do something for 1 second
}
}
public void another_O_n_algorithm(int n) {
for(int i = 0; i < n * 2; i++) {
// do something for 1 second
}
}O_n_algorithm 함수에서는 입력값(n)이 1 증가할 때마다 코드의 실행 시간이 1초씩 증가한다.
즉 입력값이 증가함에 따라 같은 비율로 걸리는 시간이 늘어난다.
그에 반해 another_O_n_algorithm은 입력값이 1 증가할 때마다 코드의 실행시간이 2초씩 증가한다. (n * 2)
another_O_n_algorithm의 시간복잡도를 O(2n)으로 생각할 수 있으나 해당 알고리즘 또한 Big-O의 표기법으로 O(n) 으로 표기된다.
이렇게 표기되는 이유는 데이터 입력값(n)이 충분히 크다고 가정하고 있고, 알고리즘의 효율성 또한 데이터 입력값(n)의 크기에 따라 영향을 받기에 상수항은 무시하기 때문이다.
O(log n) : 이진트리
O(n^2) : 이중 for 문, 삽입정렬, 거품정렬, 선택정렬
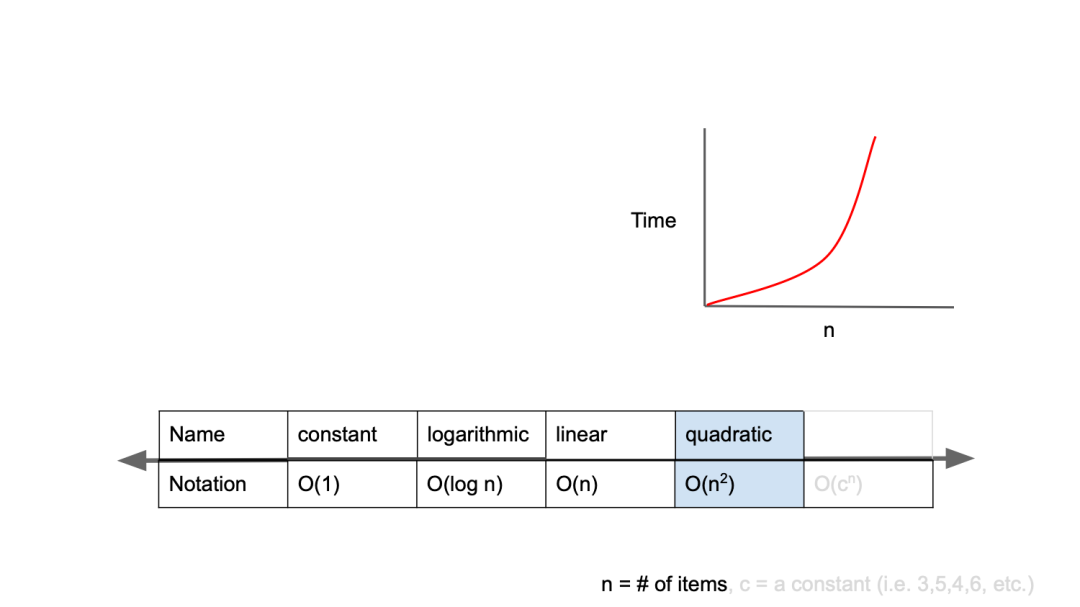
O(n^2)은 2차 복잡도(quadratic complexity)라고 부르며,입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미한다.
public void O_quadratic_algorithm(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
// do something for 1 second
}
}
}
public void another_O_quadratic_algorithm(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
for(int k = 0; k < n; k++) {
// do something for 1 second
}
}
}
}- 예를 들어 입력값이 1일 경우 1초가 걸리던 알고리즘에 5라는 값을 주었더니 25초가 걸리게 된다면, 이 알고리즘의 시간 복잡도는
O(n^2)이라고 한다. - 2n, 5n을 모두 O(n)이라고 표현하는 것처럼, n이 커질수록 지수가 주는 영향력이 점점 퇴색되기에
O(n^2)으로 표현한다.
O(2^n) : 피보나치 수열
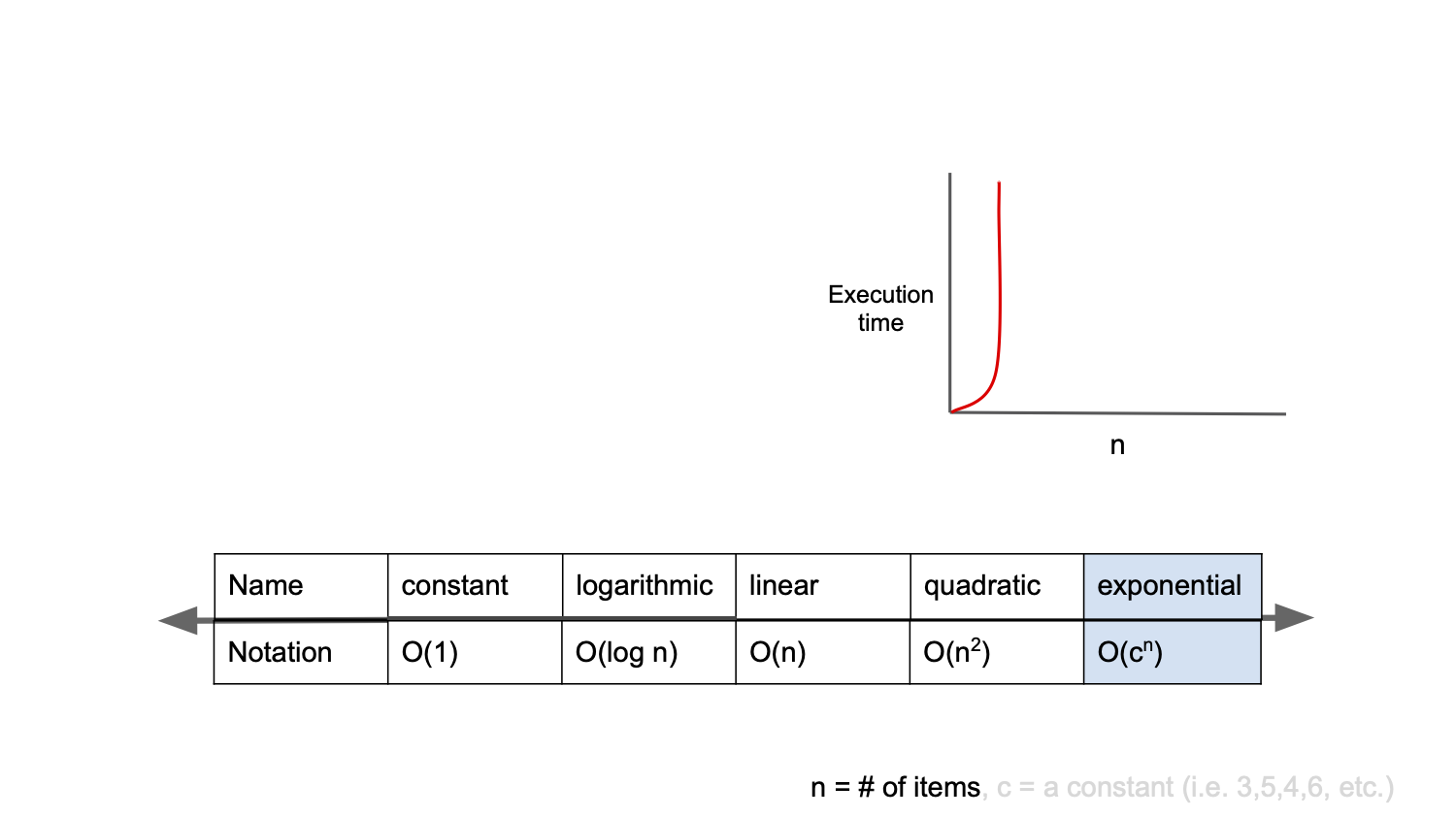
O(2^n)은 exponential complexity라고 부르며 Big-O 표기법 중 가장 느린 시간 복잡도를 가진다.
public int fibonacci(int n) {
if(n <= 1) {
return 1;
}
return fibonacci(n-1) + fibonacci(n-2);
}구현한 알고리즘이 O(2^n)의 시간복잡도를 가진다면,, 다른 접근 방식을 고려하는 것이 좋다고 한다.
