C#_11 Hashtable, Dictionary, Graph

SeonggyuMin·2025년 3월 31일

CSharp

목록 보기
9/12

1. Hashtable

1. Hashtable이란

해시테이블 (HashTable)이란 키 값을 해시함수로 해싱하여 해시테이블의 특정 위치로 직접 엑세스하도록 만든 방식이다.
또한 해시란 임의의 길이를 가진 데이터를 고정된 길이를 가진 데이터로 매핑하는 것이다.

해시함수란 키값을 해싱하여 고유한 index를 만드는 함수
조건으로 하나의 키값을 해싱하는 경우 반드시 항상 같은 index를 반환해야 한다.

대표적인 해시함수로 나눗셈법이 있다.
예시 : 2581 → (2581 % 1000) = 581

hash brown이라는 감자 잙게 다진 요리 이름이 있듯이 hash는 정보를 뭉쳐서 압축하는 과정이다.

2. Hashtable 주의점

해시테이블의 시간복잡도는 다음과 같다

<해시테이블 시간복잡도>
접근 탐색 삽입 삭제
X O(1) O(1) O(1)

그러나 해시테이블은 삽입 및 제거가 빈번할 시 효율이 좋지 않다. 충돌이 일어날 시 그를 처리하는 과정에 비용이 발생하기 때문이다.

해시 테이블은 서로 충돌할 수 있어 주의가 필요하다. 여기서 충돌이란 해시함수가 서로 다른 입력 값에 대해 동일한 해시테이블 주소를 반환하는 것이다. 모든 입력 값에 대해 고유한 해시 값을 만들 수는 없어 충돌은 불가피하다.

충돌이 일어난 해시테이블을 삭제 시 그 칸을 그냥 비워둘 수는 없다. 해당 칸을 비우면 충돌 때문에 이동한 요소를 찾을 수 없어 삭제된 칸을 막아둔다. 따라서 빈번한 삽입 삭제 시 공간 효율도가 떨어진다. => 삽입과 삭제를 빈번히 하지 않을 때 효율적이다.

충돌 해결 방안으로는 2가지 방법이 있다.

  1. 개방주소법
    해시 충돌이 발생하면 다른 빈 공간에 데이터를 삽입하는 방식이다. 해시 충돌 시 선형탐색, 제곱탐색, 이중해시 등을 통해 다른 빈 공간을 선정한다.

장점으로는 추가적인 저장공간이 필요하지 않음, 삽입삭제시 오버헤드가 적다.
단점으로는 해시테이블에 자료사용률에 따른 성능저하가 발생한다.

  1. 체이닝
    해시 충돌이 발생하면 연결리스트로 데이터들을 연결하는 방식이다.

장점으로는 해시테이블에 자료사용률에 따른 성능저하가 적다.
단점으로는 해시테이블 외 추가적인 저장공간이 필요, 삽입삭제시 오버헤드가 발생한다.

3. 해시테이블의 효율

해시테이블의 공간 사용률이 높을 경우(통계적으로 70% 이상) 급격한 성능저하가 발생한다. 이런 경우 재해싱을 통해 공간 사용률을 낮추어 다시 효율을 확보한다.
재해싱 : 해시테이블의 크기를 늘리고 테이블 내의 모든 데이터를 다시 해싱하여 보관하는 것.

2. Dictionary

1. Dictionary<T key, T value>

Dictionary<T key, T value>는 해시테이블 기반의 자료구조이다. 또한 제네릭 컬렉션 중 하나이다. 이는 중복을 허용하지 않는 key를 기준으로 해싱을 통한 빠른 탐색의 value 저장소이다.

Dictionary<string, Monster> monsters = new Dictionary<string, Monster>();

	// 추가: O(1)
	monsters.Add("피카츄", new Monster("피카츄", 1));
	monsters.Add("라이츄", new Monster("라이츄", 2));
	monsters.Add("파이리", new Monster("파이리", 3));
	monsters.Add("꼬부기", new Monster("꼬부기", 4));

	// 똑같은 키값은 추가할 수 없음
	// monsters.Add("피카츄", new Monster("피카츄", 5));
	monsters.TryAdd("피카츄", new Monster("피카츄", 1)); // 이미 키 값이 있을 때 추가하지 않음

	// 삭제: O(1)
	// Remove() 결과값은 bool 형태로 반환
	monsters.Remove("피카츄");

	// 접근은 인덱스로 접근할 수 없음

	// 탐색: O(1)
	monsters.ContainsKey("파이리");
	// TryGetValue()
	monsters.TryGetValue("파이리", out Monster monster);


	// 추가할 때 안전하게 하는 방법
	if (!monsters.ContainsKey("피카츄"))
	{
		monsters.Add("피카츄", new Monster("피카츄", 1));
	}

	monsters.TryAdd("리자몽", new Monster("리자몽", 5));

	// 인덱서를 통한 간략한 사용
	Monster find = monsters["파이리"]; // 인덱스는 아니지만 키 값으로 접근, 키 값이 없으면 오류임
	monsters["피카츄"] = new Monster("피카츄", 1);

Dictionary의 시간 복잡도는 다음과 같다.

<Ditctionary 시간복잡도>
접근 탐색 삽입 삭제
X O(1) O(1) O(1)

특성 또한 해시테이블을 기반으로 한 자료구조이다보니 잦은 삽입 및 제거에는 비효율적이다. 성능저하를 방지하기 위해 크기를 크게 잡아두는 것이 좋다.

2. 주요 메서드 및 프로퍼티

Add(key, value): 새 키-값 쌍 추가 (이미 존재하는 키면 예외 발생)
Remove(key): 해당 키의 항목 제거
ContainsKey(key): 키 존재 여부 확인
ContainsValue(value): 값 존재 여부 확인
TryGetValue(key, out value): 키가 존재하면 값을 가져오고 true 반환
Clear(): 모든 요소 제거
Count: 요소 개수 반환
Keys, Values: 키 또는 값들의 컬렉션 반환

3. Graph

1. Graph

그래프란 정점의 모음과 이 정점을 잇는 간선의 모음의 결합이다.

  • 특징
  1. 한 노드에서 출발하여 다시 자기 자신의 노드로 돌아오는 순환구조를 가짐
  2. 간선의 방향성에 따라 단방향 그래프, 양방향 그래프가 있음
  3. 간선의 가중치에 따라 연결 그래프, 가중치 그래프가 있음

정점은(node, vertex) 데이터를 담는 점을 의미한다.
간선 (Edge) 정점 간의 연결선을 의미한다.
가중치(Weight)는 간선에 부여된 비용/거리/시간 등의 값을 의미한다.

그래프는 트리라는 하위개념을 포함하고 있다. 트리 ⊂ 그래프의 구조이다.

항목그래프 (Graph)트리 (Tree)
구조비계층적 구조계층적 구조 (부모 → 자식)
방향성방향 그래프 / 무방향(쌍방향) 그래프 모두 가능단방향 (부모 → 자식)
사이클사이클 허용사이클 없음
연결성연결되지 않은 노드 존재 가능항상 연결되어 있음
간선 수제한 없음간선 수 = 노드 수 - 1
경로 수두 노드 간 경로가 여러 개일 수 있음두 노드 간 경로는 정확히 하나만 존재함

그래프는 정돈되지 않은 모습과 흡사하고, 트리는 조직도 혹은 윈도우의 폴더 구조와 같이 정돈된 모습과 흡사하다.

2. 그래프 구조 구성 방법

그래프 구조를 구성하는 방법에는 크게 2가지가 있다.

1. 클래스로 구성

그래프의 속성 및 메서드를 활용한 클래스로 구성하여 사용할 수 있다.

public class GraphNode<T>
{
	private T vertex;
	public T Vertex
	{
		get { return vertex; }
		set { vertex = value; }
	}

	private List<GraphNode<T>> edge = new List<GraphNode<T>>();

	public GraphNode(T value)
	{
		this.vertex = vertex;
	}

	public void AddEdge(GraphNode<T> node)
	{
		edge.Add(node);
	}

	public void RemoveEdge(GraphNode<T> node)
	{
		// 연결 해제
		edge.Remove(node);
	}

	public bool IsConnect(GraphNode<T> node)
	{
		return edge.Contains(node);
	}   
}

internal class Program
{
	static void Main(string[] args)
	{
		GraphNode<int> node0 = new GraphNode<int>(0);
		GraphNode<int> node1 = new GraphNode<int>(1);
		GraphNode<int> node2 = new GraphNode<int>(2);
		GraphNode<int> node3 = new GraphNode<int>(3);
		GraphNode<int> node4 = new GraphNode<int>(4);
		GraphNode<int> node5 = new GraphNode<int>(5);
		GraphNode<int> node6 = new GraphNode<int>(6);
		GraphNode<int> node7 = new GraphNode<int>(7);

		// 양방향 연결
		node0.AddEdge(node3);
		node3.AddEdge(node0);

		node0.AddEdge(node4);
		node4.AddEdge(node0);
	}
}
2. 간략화 구조 방법

그래프 구조를 클래스를 구성하지 않고 간략하게 만들 수 있다.

1. 인접행렬 그래프

그래프 내의 각 정점의 인접 관계를 나타내는 행렬이며 2차원 배열을 출발정점, 도착정점으로 표현한다.
장점은 인접여부 접근이 빠르다.
단점은 메모리 사용량이 많다.

가중치 X

bool[,] matrixGraph1 = new bool[5, 5]
	{
		{ false, false, false, false,  true },
		{ false, false,  true, false, false },
		{ false,  true, false,  true, false },
		{ false, false,  true, false,  true },
		{  true, false, false,  true, false },
	};

	const int INF = int.MaxValue;


// 양방향 연결
// graph[0, 3] = true;
// graph[3, 0] = true;

Console.WriteLine($"0에서 3으로 연결되어 있는가? {graph[0, 3]}");

bool 타입의 2차원 배열을 활용하여 연결유무를 확인할 수 있다.

가중치 O

const int INF = int.MaxValue;

	// 예시 - 단방향 가중치 그래프 (단절은 최대값으로 표현)
	int[,] matrixGraph2 = new int[5, 5]
	{
		{   0, 132, INF, INF,  16 },
		{  12,   0, INF, INF, INF },
		{ INF,  38,   0, INF, INF },
		{ INF,  12, INF,   0,  54 },
		{ INF, INF, INF, INF,   0 },
	};


// graph[0, 1] = 3;
// graph[1, 3] = 5;

Console.WriteLine($"0에서 3으로 연결되어 있는가? {graph[0, 1]}");

int 2차원 배열을 활용하여 연결유무 및 가중치를 확인할 수 있다. 이때 가중치가 설정되어있지 않으면 음수 혹은 최대값(MaxValue)을 넣어 표현하기도 한다.

그래프를 인접행렬화시킨 모습이다. 해당 사이트에서 확인할 수 있다.

양방향 그래프

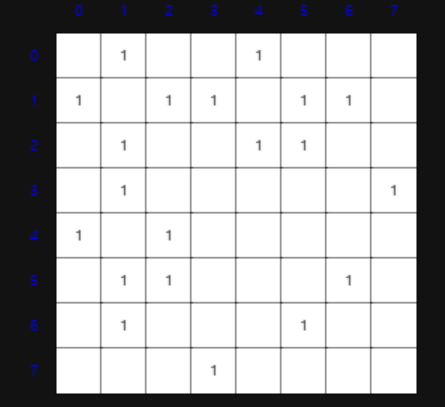
무방향 그래프(y = -x 대칭의 모습이다)

2. 인접리스트 그래프

인접리스트 그래프란 그래프 내의 각 정점의 인접 관계를 표현하는 리스트이다. 인접한 간선만을 리스트에 추가하여 관리한다.
장점은 메모리 사용량이 적다.
단점은 인접 여부를 확인하기 위해 리스트 탐색이 필요하다.

List<int>[] listGraph1; // 연결 그래프
List<(int, int)>[] listGraph2; // 가중치 그래프

listGraph1 = new List<int>[8];

listGraph1[0] = new List<int> { 2, 4 };
listGraph1[1] = new List<int> { 2, 3 };
listGraph1[2] = new List<int> { 0, 1, 4 };
listGraph1[3] = new List<int> { 1, 7 };
listGraph1[4] = new List<int> { 0, 2 };
listGraph1[5] = new List<int> { 6, 7 };
listGraph1[6] = new List<int> { 5, 7 };
listGraph1[7] = new List<int> { 3, 5, 6 };

// 다른 방법
//listGraph1[0].Add(1);
//listGraph1[1].Add(0);
//listGraph1[1].Add(3);
//listGraph1[2].Add(0);
//listGraph1[2].Add(1);
//listGraph1[2].Add(4);
//listGraph1[3].Add(1);
//listGraph1[4].Add(3);

// 연결 추가
listGraph1[0].Add(5);
listGraph1[5].Add(0);

// 연결 해제
listGraph1[1].Remove(2);
listGraph1[2].Remove(1);

// 연결 확인
bool isConnect = listGraph1[0].Contains(1);

인접 리스트에서 가중치를 표현하려면, 연결된 노드와 가중치를 함께 저장해야 하며, 이때 첫 번째 값은 도착 노드, 두 번째 값은 가중치로 사용된다.

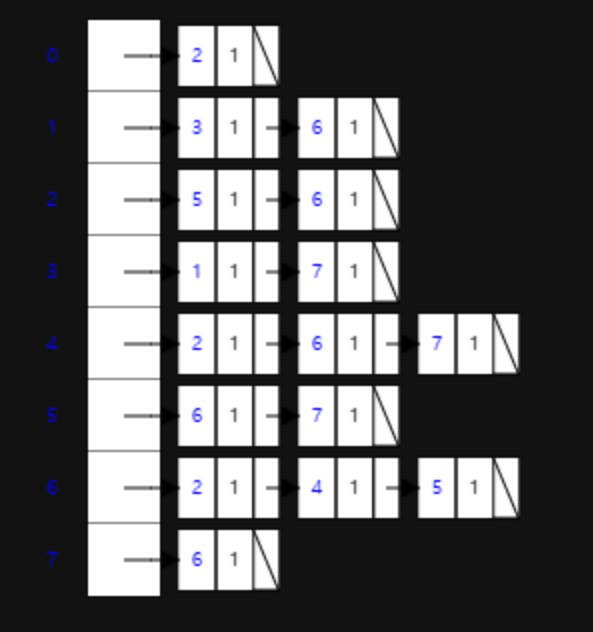
인접리스트 그래프 구조

4. 메모

그래프 구조는 다양한 곳에서 쓰일 수 있고, 기획자에게 그림의 형태로 받았을 때 코드화시키는 능력이 중요하기 때문에 이를 연습하는 것이 중요하다.

profile
SeonggyuMin
Hello~
이전 포스트

C#_10 자료구조, List, LinkedList, Stack, Queue

다음 포스트

C#_12 Algorithm, Sort

0개의 댓글