재귀
어떤 사건이 자기 자신을 포함하고 있거나 자기 자신을 사용하여 정의하고 있을 때 재귀적이라고 한다.
정수 n의 팩토리얼 n!=n x (n-1)!
class Factorial {
static int factorial(int n) {
if(n>0)
return n* factorial(n-1);
else
return 1;
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
System.out.print("정수를 입력하세요: ");
int x=sc.nextInt();
System.out.println(x + "의 팩토리얼은 " + factorial(x) + "입니다.");
}
}- 삼항 연산자 사용하기
return (n>0) ? n*factorial(n-1) : 1;
- 유클리드 호제법
두 개의 수가 주어졌을 때, 최대공약수를 구하는 알고리즘이다.
72, 42 두 개의 수로 유클리드 호제법을 사용해서 최대공약수를 구해보겠습니다.
- 먼저 두 개의 수 중 큰 수를 찾습니다. 여기서는 72입니다.
- 큰 수를 작은 수로 나눠서 나머지를 구합니다. => 72 % 42 = 30(나머지)
- 나머지를 가지고 앞에서 나눈 수를 다시 나눠서 나머지를 구합니다. => 42 % 30 = 12(나머지)
- 3번의 과정을 반복합니다. => 30 % 12 = 6(나머지)
- 3번의 과정을 반복합니다. => 12 % 6 = 0(나머지)
- 5번의 과정을 마지막으로 나머지가 0이 되었으므로 그 시점에 나눈 수가 최대공약수가 됩니다.
위의 순서대로라면 72와 42의 최대공약수는 6이 됩니다.
bn : 큰 숫자
sn : 작은 숫자
public int eucd(int bn, int sn) {
// 큰 숫자를 작은 숫자로 나눈 나머지를 계산한다.
// 큰 숫자를 작은 숫자로 나눈 값이 0이면 작은숫자 리턴, 아니면 재귀형태로 자신을 호출한다.
int r=bn%sn;
if(r==0) {
//나머지가 0이면 작은 숫자가 최대공약수이므로 작은 숫자를 리턴한다.
return sn;
} else {
// 나머지가 0 이상이면 재귀형태로 호출한다.
// 이때 파라미터는 작은 숫자와 나머지를 넣어준다.
return eucd(sn, r);
}
} - 두 정수의 최대공약수를 구하는 프로그램이다.
import java.util.Scanner;
class EuclidGCD {
static int gcd(int x, int y) {
if(y==0)
return x;
else
return gcd(y, x%y);
}
public static void main(String[] args) {
Scanner stdIn=new Scanner(System.int);
System.out.println("두 정수의 최대공약수를 구한다.");
System.out.print("정수를 입력하세요 : ");
int x=sc.nextInt();
System.out.print("정수를 입력하세요 : ");
int y=sc.nextInt();
System.out.println("최대공약수는 " + gcd(x, y) + "입니다.");
}
}
하노이의 탑
쌓아 놓은 원반을 최소 횟수로 옮기기 위한 알고리즘이다.
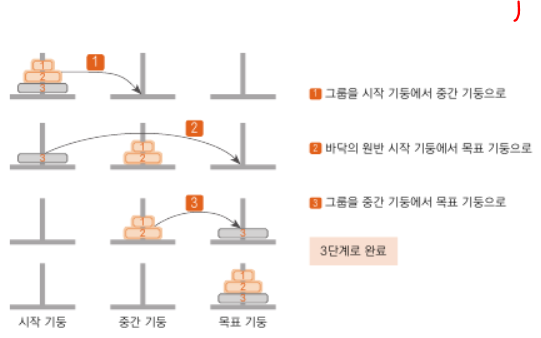
no 옮겨야 할 원반의 개수
x : 시작 기둥 번호
y : 목표 기둥 번호
그룹을 사용해도 된다.
그룹으로 보면 3단계로 구현할 수 있다.
move메서드의 매개변수 no은 옮겨야 할 원반의 개수,
x는 시작 기둥의 번호
y는 목표 기둥의 번호이다.
move(n, 1, 3); 1번기둥에 쌓인 n개의 원반을 3번 기둥으로 옮긴다.
기둥 번호를 1, 2, 3으로 나타낸다. = 6 합
중간 기둥 6-x-y로 구할 수 있다. move메서드는 no개의 원반을 3단계로 옮긴다.
if(no >1)
move(no-1, x, 6-x-y);
첫번째에서 중간으로
move(no-1, 6-x-y, y);
중간에서 끝으로
class Hanoi {
static void move(int no, int x, int y) {
if(no > 1)
move(no-1, x, 6-x-y);
System.out.printf("원반[%d]을 %d번 기둥에서 %d번 기둥으로 옮긴다.", no, x, y);
if(no>1)
move(no-1, 6-x-y, y);
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
System.out.println("하노이의 탑");
System.out.print("원반의 개수 : ");
int n=sc.nextInt();
move(n, 1, 3); //1번 기둥에서 3번 기둥으로 옮긴다. 8퀸 문제
작은 문제로 나누어 해결 서로 공격하여 잡을 수 없도록 8개의 퀸을 8x8체스판에 놓는다.
각 열에 1개의 퀸을 배치하는 조합을 재귀를 사용하여 나열한다.
체스판의 어떤 지점으로든 여덟 방향으로 직선 이동이 가능하다.
8개의 퀸을 배치 체스판의 크기 8x8 64칸으로
퀸을 1개 배치하면 63칸이 된다.
8번째 까지 생각하면
64x63 x62x 61 x60 x59 x58x 57 =178,462, 987,637,760가지 조합이 가능
각 열에 퀸을 1개만 배치 가능하다.
규칙1. 각 열에 퀸을 1개만 배치 가능
8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 = 16,777,216 가지
규칙2. 각 행에 퀸을 1개만 배치
경우의 수가 더 감소한다.
0열에서 퀸의 배치 방법은 8가지이다.
가지 뻗기 (=분할 해결법)
규칙1을 적용하여 각 열에 1개의 퀸을 배치하는 조합을 재귀적으로 나열한 것이다.
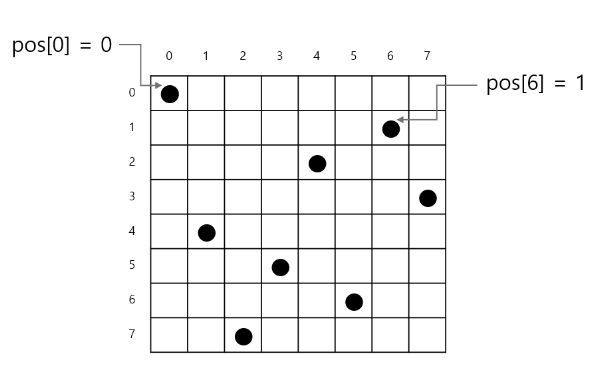
class QueenB {
static int[] pos=new int[8]; // 각 열에 있는 퀸의 위치
// 각 열에 있는 퀸의 위치를 출력
static void print() {
for(int i=0; i<8; i++)
System.out.printf("%2d", pos[i]);
System.out.println();
}
static void set(int i) {
for(int j=0; j<8; j++){
pos[i]=j; // 퀸을 j행에 배치
if(i==7) // 모든 열에 배치
print();
else
set(i+1); // 다음 열에 퀸을 배치한다.
}
}
public static void main(String[] args){
set(0); //0열에 퀸을 배치
}
}