Do it 자료구조와 함께 배우는 알고리즘 입문 - 06. 정렬 알고리즘

- 정렬 알고리즘

대소 관계에 따라 데이터 집합을 일정한 순서로 나열하는 작업을 말한다.
안정된 정렬이란 키 값이 같은 요소의 순서가 정렬 전후에도 유지되는 것을 말한다.

• 내부 정렬 : 정렬할 모든 데이터를 하나의 배열에 저장할 수 있을 때에 사용하는 알고리즘
• 외부 정렬 : 정렬할 데이터가 너무 많아서 하나의 배열에 저장할 수 없을 때에 사용하는 알고리즘

정렬 알고리즘의 핵심 요소는 교환, 선택, 삽입이다.

1. 버블 정렬

이웃한 두 요소의 대소 관계를 비교하고 필요에 따라 교환을 반복하는 알고리즘으로 단순 교환 정렬이다.

static void swap(int[] a, int idx1, int idx2) {
	int t=a[idx1];
    a[idx1]=a[idx2];
    a[idx2]=t;
}

static void bubbleSort(int[] a, int n) {
	for(int i=0; i<n-1; i++)
    	int exchg=0;
    	for(int j=n-1; j>i; j--)
        	if(a[j-1]>a[j]) {
            	swap(a, j-1, j);
                exchg++;
            }
        if (exchg==0) break; //교환이 이루어지지 않으므로 멈춘다.
    }
}

교환 횟수의 평균값은 비교 횟수의 절반인 n(n-1)/4회이다.
이동 횟수의 평균은 3n(n-1)/4회이다.

2. 단순 선택 정렬

가장 작은 요소를 맨 앞으로 이동하고, 두 번째 작은 요소는 맨 앞에서 두 번째로 이동하는 등
작업을 반복하는 알고리즘이다.

1) 가장 작은 값의 요소인 1을 선택하여 첫번째 값과 교환한다.
2) 두 번째로 작은 요소를 선택하여 값을 교환한다.
3) 앞에서 진행한 작업을 반복한다.

static void selectionSort(int[] a, int n) {
	for (int i=0; i<n-1; i++) {
    	int min=i; // 아직 정렬되지 않은 부분에서 가장 작은 요소의 인덱스 저장 
        for(int j=i+1; j<n; j++)
        	if(a[j] < a[min])
            	min=j;
            swap(a, i, min); // 정렬되지 않은 부분의 첫 요소와 가장 작은 요소를 교환
    }
}

단순 선택 정렬 알고리즘의 요솟값을 비교하는 횟수 : (n2-n)/2번이다.

3. 단순 삽입 정렬 O(n^2)

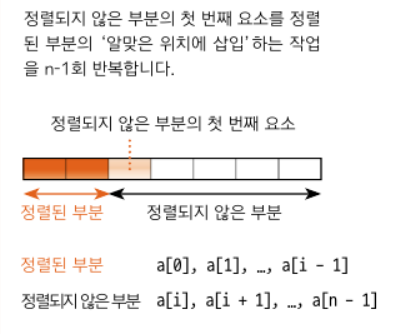
선택한 요소를 그보다 더 앞쪽의 알맞은 위치에 삽입하는 작업을 반복하여 정렬하는 알고리즘이다.

• 단순 삽입 정렬
  6 4 1 7 3 9 8
  1) 두 번째 요소부터 선택하여 진행한다. 작다면 앞쪽에 삽입한다.
  정렬된 부분과 아직 정렬되지 않은 부분으로 배열이 구성되어 있다고 생각하고, n-1회 반복하면서 정렬을 마친다.

for(int i=1; i<n; i++) {
	// tmp = a[i]
    // a[0], a[i-1]의 알맞은 곳에 tmp삽입한다
}

static void insertionSort(int[] a, int n) {
	for(int i=1; i<n; i++) {
    	int j;
        int tmp=a[i];
        for(j=i j>0 && a[j-1]>tmp; j--) // tmp보다 작은 요소를 만날 때까지 
        	a[j]=a[j-1];
        a[j]=tmp;
    }
}

4. 셀 정렬 (= 단순 삽입 정렬 보완한)

단순 삽입 정렬의 장점을 살리고 단점을 보완하여 좀 더 빠르게 정렬하는 알고리즘
정렬이 되었거나, 또는 그 상태에 가까우면 정렬 속도가 아주 빠르다.
삽입할 곳이 멀리 떨어지면 이동(대입)하는 횟수가 많다.

1 2 3 4 5 0 6 에서
0보다 작은 요소를 만날 때까지 하나 왼쪽 요소를 대입하여 비교한 뒤 맨 앞에 0을 대입한다.

5. 퀵 정렬

가장 빠른 정렬 알고리즘 중 하나로 널리 사용되고 있다.
알고리즘의 정렬 속도가 매우 빠른 데서 착안해 직접 붙인 이름이다.

키가 168cm인 학생 A를 선택하여 학생을 기준으로
A의 키보다 작은 사람의 그룹과 큰 사람의 그룹으로 나눈다.

배열을 두 그룹으로 나누기
피벗 x를 가운데로 놓고
왼쪽 끝 요소의 인덱스 pl, 오른쪽 끝 요소의 인덱스 pr를 놓는다.
a[pl]>=x가 성립하는 요소를 찾을 때까지 pl을 오른쪽으로 스캔한다.
a[pr]<=x가 성립하는 요소를 찾을 때까지 pr을 왼쪽으로 스캔한다.
피벗에서 왼쪽과 오른쪽 커서를 교차하게 한다.

• 피벗 이하의 그룹 : a[0] ~ a[pl-1]
• 피벗 이상의 그룹 : a[pr+1] ~ a[n-1]

피벗과 같은 값을 갖는 그룹 : a[pl-1] ~ a[pr+1]

class Parition {
	static void swap(int[] a, int idx1, int idx2) {
    	int t=a[idx1];
        a[idx1]=a[idx2];
        a[idx2]=t;
  	} // 값을 교환한다.
    
    static void quickSort(int[] a, int left, int right) {
		int pl=left;
        int pr=right;
        int x = a[(pl+pr)/2]; // 피벗(가운데 요소)
        
        do {
        	while (a[pl] < x)pl++;
            while (a[pr] > x)pl--;
            if(pl <= pr)
            	swap(a, pl++, pr--);
       }while(pl<=pr);
       
       if(left < pr) quickSort(a, left, pr);
       if(pl 
      
    

6. 병합 정렬

병합 정렬은 배열을 앞부분과 뒷부분 둘로 나누어 각각 정렬한 다음 병합하는 작업을 반복하여 정렬하는 알고리즘이다.

= 병합에 필요한 시간 복잡도는 O(n)이다.

• 정렬을 마친 두 배열의 병합을 살펴보기
  정렬을 마친 두 배열의 병합을 살펴본다.

각 배열의 작업에서 선택한 요소의 인덱스는 pa, pb, pc이다.
배열 a에서 선택한 요소 a[pa]와
배열 b에서 선택한 요소 b[pb]를 비교하여
배열 c에 작은쪽값을 c[pc]에 저장한다. for문을 돌려서 배열을 완성시킨다.

public class MergeArray {

    static void merge(int[] a, int na, int[] b, int nb, int[] c){
        int pa=0;
        int pb=0;
        int pc=0;

        while(pa < na && pb < nb) // 작은 쪽 값을 C에 저장
            c[pc++] = (a[pa] <= b[pb]) ? a[pa++] : b[pb++];
        // 작은 쪽 값을 c에 a[pa++]를 한다.

        while (pa < na)
            c[pc++] = a[pa++]; // a에 남아 있는 요소를 복사

        while (pb < nb)
            c[pc++] = b[pb++]; // b에 남아 있는 요소를 복사한다.
    }

    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        int[] a={2, 4, 6, 8, 11, 13};
        int[] b={1, 2, 3, 4, 9, 16, 21};
        int[] c=new int[13]; // 생성

        System.out.println("두 배열을 병합");

        merge(a, a.length, b, b.length, c);
        System.out.println("배열 a와 b를 병합하여 배열 c에 저장");
        System.out.println("배열 a: ");
        for(int i=0; i<a.length; i++)
            System.out.println("a[" + i + "] = " + a[i]);

        System.out.println("배열 b: ");
        for(int i=0; i<b.length; i++)
            System.out.println("a[" + i + "] = " + b[i]);

        System.out.println("배열 c: ");
        for(int i=0; i<c.length; i++)
            System.out.println("a[" + i + "] = " + c[i]);
    }
}

Arrays.sort 사용하기 (퀵, 병합 정렬)

배열을 정렬할때 sort()메소드를 사용하면 쉽게 정렬을 할 수 있다.

public class ArraysSortTester {
    // 퀵 정렬
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);

        System.out.print("요솟수: ");

        int num=sc.nextInt();
        int[] x=new int[num]; // 길이가 num인 배열

        for(int i=0; i<num; i++){
            System.out.print("x[" + i +"]: ");
            x[i]=sc.nextInt();
        }

        Arrays.sort(x); //배열 x를 정렬

        System.out.println("오름차순으로 정렬한다.");
        for(int i=0; i<num; i++)
            System.out.println("x[" + i + "]=" + x[i]);
    }
}

비재귀적인 퀵 정렬 구현하기

static void quickSort(int[] a, int left, int right) {
	IntStack lstack=new IntStack(right-left+1); //스택의 생성
    IntStack rstack=new IntStack(right-left+1); 
    
    lstack.push(left);
    rstack.push(right);
    
    while (lstack.isEmpty() != true) {
    	int pl=left=lstack.pop(); // 왼쪽 커서
        int pr=right=rstack.pop(); // 오른쪽 커서
        int x=a[(left+right)/2]; // 피벗(가운데)
        
        do {
        	while (a[pl] <x) pl++;
            while (a[pr] >x) pl--;
            if(pl<=pr)
            	swap(a, pl++, pr--);
        } while (pl<=pr);
        
        if(left < pr) {
        	lstack.push(left); // 왼쪽 그룹 범위의
            rstack.push(pr); // 인덱스를 푸시
        }
        if(pl < right) {
        	lstack.push(pl); // 오른쪽 그룹 범위의
            rstack.push(right); // 인덱스를 푸시
        }
     } 
  } 

7. 힙 정렬

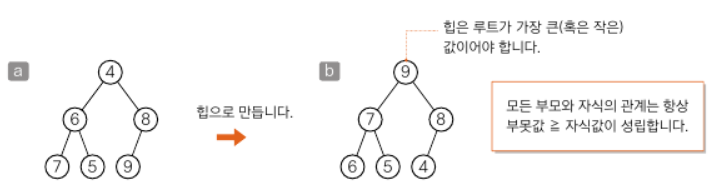
heap힙을 사용하여 정렬하는 알고리즘이다. 부못값이 자식값보다 항상 크다 라는 조건을 만족하는 완전 이진트리를 말한다.

부못값 >= 자식값을 만족하는 트리를 만들어준다.

부모 : a[(i-1)/2]
왼쪽 자식 : a[i*2+1]
오른쪽 자식 : a[i*2+2]

• 힙에서 가장 큰 값인 루트를 꺼낸다.
• 루트 이외의 부분을 힙으로 만든다.

8. 도수 정렬

요소의 대소 관계를 판단하지 않고 빠르게 정리 가능하다.

두 요소의 키 값을 비교하지 않아도 된다.

1) 도수분포표 만들기
배열 a={5, 7, 0, 2, 4, 10, 3, 1, 3}
각 점수에 해당하는 학생이 몇명인지를 나타내는 배열

배열 f을 사용한다. 배열 f의 모든 요솟값을 0으로 초기화한다.

2) 누적도수분포표 만들기
0점부터 n점까지 몇 명의 학생이 있는지 누적한 값을 나타내는 누적도수분포표
for(int i=1; i<=max; i++)
f[i] += f[i-1];

3) 목표 배열 만들기
각각의 점수를 받은 학생이 몇 번째에 위치하는지 알 수 있으므로 이 시점에서 정렬은 거의 마쳤다.
for(int i=n-1; i>=0; i--)
b[--f[a[i]]] = a[i];

배열 a의 요소를 마지막 요소부터 처음까지 스캔한 뒤 배열 f와 대조한다.
요소 a[7]

4) 배열 복사하기

for(int i=0; i<n; i++)
a[i]=b[i];