트리
트리와 트리를 구성하는 요소는 노드(node)와 가지(edge)이다.
루트 : 트리의 가장 윗부분에 위치하는 노드를 루트라고 한다. 하나의 트리에는 하나의 루트만 있다. 나무 모양과 비슷하다는 것을 알 수 있다:D
- 리프 : 가장 아랫부분에 위치하는 노드
- 안쪽 노드 : 리프를 제외한 나머지 노드
- 자식 : 가지로 연결된 아래쪽 노드
- 부모 : 가지로 연결된 위쪽 노드
- 형제 : 부모가 같은 노드
- 차수 : 노드가 갖는 자식의 수
- 높이 : 루트에서 가장 멀리 떨어진 리프까지 거리
- 널 트리 : 노드가 전혀 없는 트리
순서 트리
1) 너비 우선 탐색(가로형 탐색)
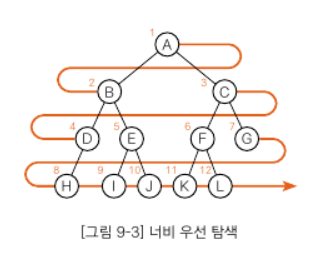
왼쪽 -> 오른쪽 방향으로 탐색
A->B->C->D->E->F->G->H->I->J->K->L
2) 깊이 우선탐색(세로형 탐색)
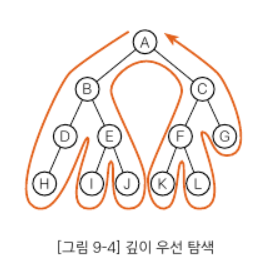
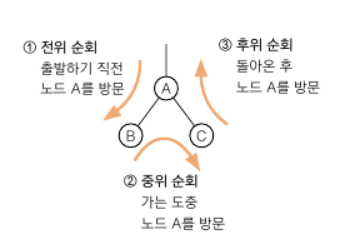
리프에 이를 때까지 아래로 내려가면서 탐색한다. 도달할 곳이 없으면 부모에게 돌아간다.
-
전위 순회
노드 방문 -> 왼쪽 -> 오른쪽
A->B->D->H->E->I->J->C->F->K->L->G -
중위 순회
왼쪽 자식 -> 노드 -> 오른쪽
H->D->B->I->E->J->A->K->F->L->C->G -
후위 순회
왼쪽 자식 -> 오른쪽 -> 노드
H->D->I->J->E->B->K->L->F->G->C->A
이진트리
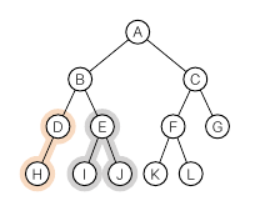
각 노드가 왼쪽 자식과 오른쪽 자식 둘을 갖는 트리
- 완전이진트리
루트에서 아래쪽 레벨로 내려가는 노드가 빠짐없이 채워져 있고, 같은 레벨도 빠짐없이 채워져 있는 이진트리
높이가 K인 완전이진트리가 가질 수 있는 노드의 최댓값 : 2K+1-1개
이진검색트리
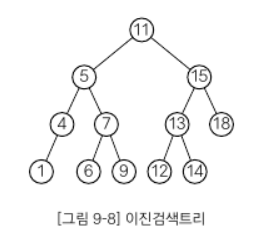
구조가 단순하다,
중위 순회를 하면 키값의 오름차순으로 노드를 얻을 수 있다.
이진 검색과 비슷한 방식으로 아주 빠르게 검색할 수 있다.
노드를 삽입하는 것이 쉽다.
- 중위 순회
1->4->5->6->7->9->11->12->13->14->15->18
class Node<K, V>{
K key; // 키값
V data; // 데이터
Node<K, V> left; // 왼쪽 포인터 K
Node<K, V> right; // 오른쪽 포인터 V
}
- 이진검색트리
public class BinTree<K,V> {
// 노드
static class Node<K, V> {
private K key; // 키값
private V data; // 데이터
private Node<K, V> left; // 왼쪽 포인터(왼쪽 자식노드에 대한 참조)
private Node<K, V> right; // 오른쪽 포인터(오른쪽 자식노드에대한 참조)
// 생성자
Node(K key, V data, Node<K,V> left, Node<K,V> right) {
this.key=key;
this.data=data;
this.left=left;
this.right=right;
}
// 키값을 반환
K getKey() {
return key;
}
// 데이터를 반환
V getValue() {
return data;
}
void print() {
System.out.println(data);
}
}
private Node<K, V> root; // 루트
private Comparator<? super K> comparator = null; // 비교자 Comparator<? super K>Java에서 제공하는 인터페이스인 Comparator를 사용하여 노드의 키 값(K)을 비교할 때 사용하는 객체이고 이 인터페이스는 키 값의 대소 관계를 판단할 수 있다. 비교자를 명시적으로 설정하지 않으면 자동으로 null이되도록 선언한다. ?는 그냥 아무 타입을 나타낸다. K와 비교를 수행한다.
public BinTree() {
root=null; // 자연 순서에 따라 키값을 비교한다. 노드가 하나도 없는(비어 있는) 이진검색트리를 생성한다.
}
public BinTree(Comparator<? super K> c) {
this(); // 비교자로 키값을 비교한다.
comparator=c;
}- search 메서드
선택 노드를 p로 한다. p=null이면 검색 실패
key와 선택 노드 p의 값을 비교한다.
값이 같으면 검색에 성공한다.
public V search(K key) {
Node<K,V> p=root; //루트에 주목
while(true) {
if(p==null)
return null; // 검색 실패
int cond=comp(key, p.getKey()); // key와 p의 키값을 비교한다.
if(cond==0) 같으면
return p.getValue(); // 검색 성공
else if(cond<0)
p=p.left; // 왼쪽 서브트리에서 검색
else
p=p.right; // 오른쪽 서브트리에서 검색
}
}
- add 노드를 삽입
1) 서브트리의 루트를 선택한다. 선택 노드를 node로 한다.
2) 삽입할 키 key와 선택 노드 node의 키값을 비교한다. 값이 같으면 삽입에 실패 = 종료
key<삽입할 값
왼쪽에 없다면 노드를 삽입 = 종료
노드가 있다면 그 왼쪽 자식 노드로 간다.
key>삽입할 값
오른쪽에 없다면 노드를 삽입 = 종료
노드가 있다면 그 오른쪽 자식 노드로 간다.
