최소 스패닝 트리

첫 알고리즘 블로그

크루스칼 알고리즘

가중치가 높은 간선을 제거하면서 최소 비용 신장 트리를 만드는 알고리즘

순서

예시

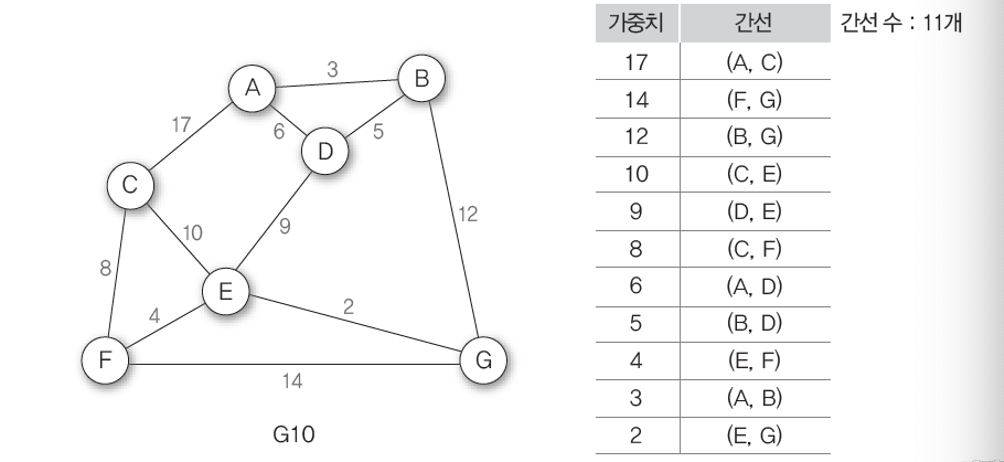
0. 초기 상태는 그래프의 가중치를 따라 내림차순으로 정렬한다.

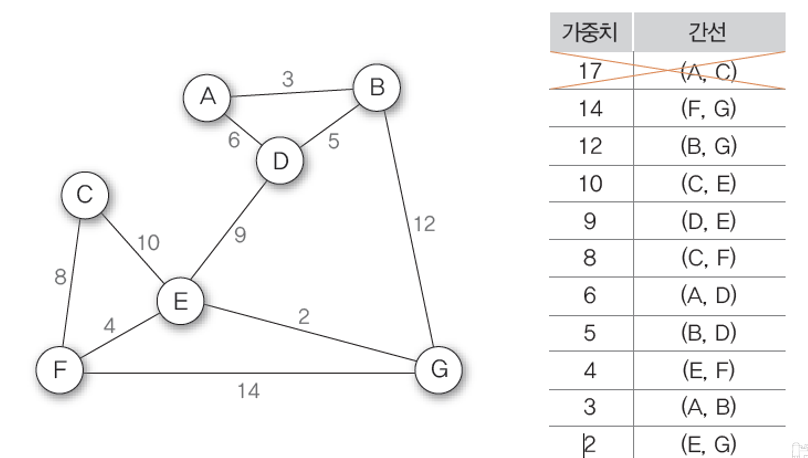
1. 가장 높은 가중치의 간선을 제거한다.
=> 가중치가 17인 간선(A,C) 제거

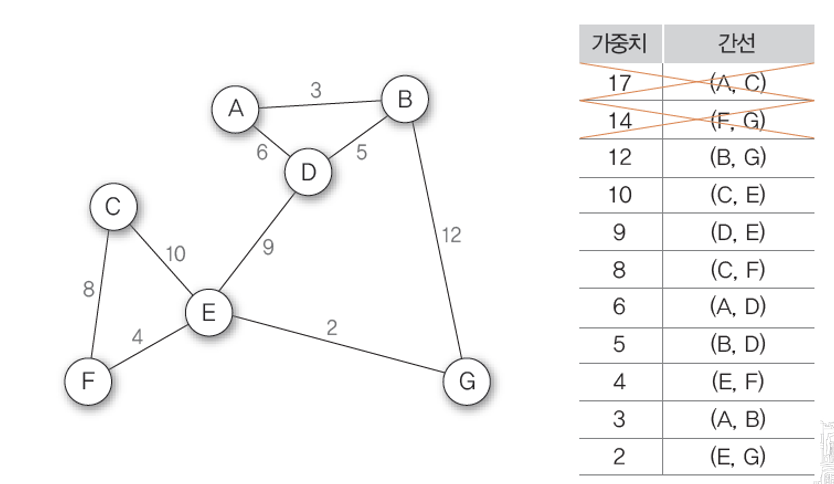
2. 다음으로 높은 가중치의 간선을 제거한다.
=> 가중치가 14인 간선(F,G)제거

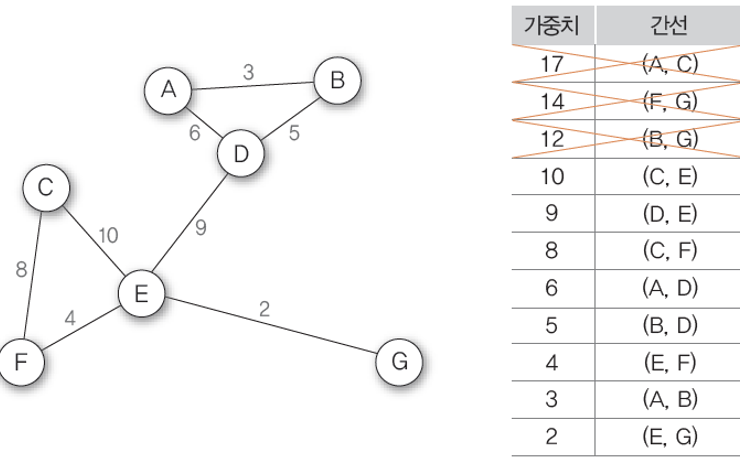
3. 남은 간선 중 가중치가 가장 높은 간선 (B,G)를 제거한다.

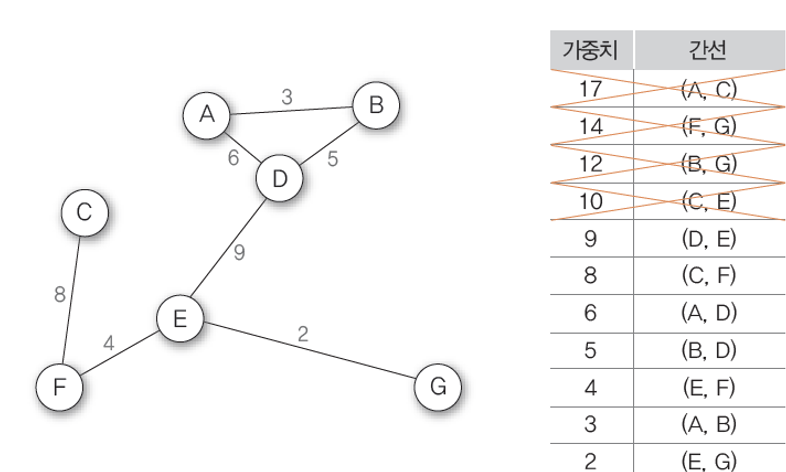
4. 남은 간선 중 가중치가 가장 높은 간선 (C,E)를 제거한다.

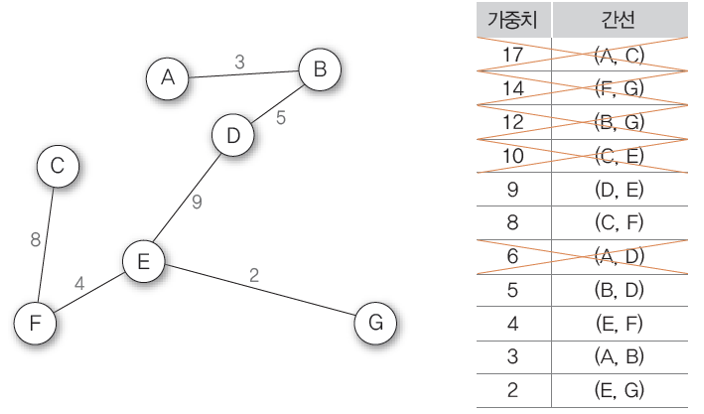
5.남은 간선 중 가중치가 가장 높은 간선 (D,E)를 제거하면 그래프가 분리되어 단절 그래프가 된다. 그 다음으로 높은 가중치의 간선 (C,F)를 제거한다. 하지만 (C,F)를 제거하면 정점 C가 분리되므로 제거할 수 없다. 그러므로 다음으로 가중치가 높은 간선 (A,D)를 제거한다.

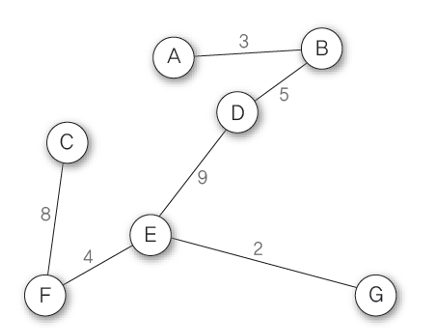
6. 현재 남은 간선 수가 6개이므로 정점 7개, 간선 6개로 알고리즘 수행을 종료하면 신장 트리가 완성된다.

알고리즘 문제

최소 스패닝 트리

백준에서 최소 스패닝 트리의 기본문제를 가져와봤다.

V,E = map(int,input().split())
root = [i for i in range(V+1)]
edge = [] # 간선리스트
for i in range(E): 
  edge.append(list(map(int,input().split())))

# 비용을 기준으로 오름차순
edge.sort(key=lambda x:x[2])

def find(x):
  if x!=root[x]:
    root[x] = find(root[x])
  return root[x]

ans = 0 
for a,b,c in edge:
  aRoot = find(a)
  bRoot = find(b)
  if aRoot != bRoot:
    if aRoot > bRoot:
      root[aRoot] = bRoot
    else:
      root[bRoot] = aRoot
    ans += c

print(ans) 

find함수

주어진 노드 x의 최상위 부모(루트노드)를 찾는다. 경로 압축을 통해 트리의 높이를 줄이는 역할을 한다.

크루스칼을 이용한 MST

• 간선 리스트를 순회하며, 각 간선이 두 정점(a,b)를 연결한다. 각 정점의 부모 노드를 찾고, 부모 노드가 다르면 두 노드를 합친다. 이때 가중치 c를 ans에 더한다.
• 두 정점의 부모가 다르면, 사이클을 생성하지 않으므로 간선을 MST에 포함시킨다.
• 큰 root값을 작은 root값으로 만드는 건 큰 가중치의 간선부터 삭제하는 크루스칼의 특징을 보여준다.