[논문리뷰] LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation (2020)

sungyeon park·2022년 10월 4일

GNN Gowalla LightGCN Paper Recommendation

RecSys

목록 보기

1/2

세 줄 요약

collaborative filtering의 성능을 저하시키는 기존 GCN 구조 (feature transformation, nonlinear activation) 의 단순화를 목적으로 함
neighborhood aggregation과 같은 주 요소만 포함한 LightGCN을 제안
SOTA GCN-based recommender 보다 향상된 결과를 보임

Problem definition

GCN은 node feature가 풍부한 그래프의 node classification 태스크에 주로 이용되는 방법론
하지만, CF를 위한 user-item interaction graph에서 각 node는 ID embedding으로 이루어짐 (no concrete semantic)
따라서, GCN의 feature transformation 과 nonlinear activation은 Neural Graph Collaborative Filtering (NGCF)에 거의 기여하는 바가 없음

Solution

LightGCN은 GCN의 가장 중요한 요소인 neighborhood aggregation 만을 포함하도록 함

Empirical Explorations on NGCF

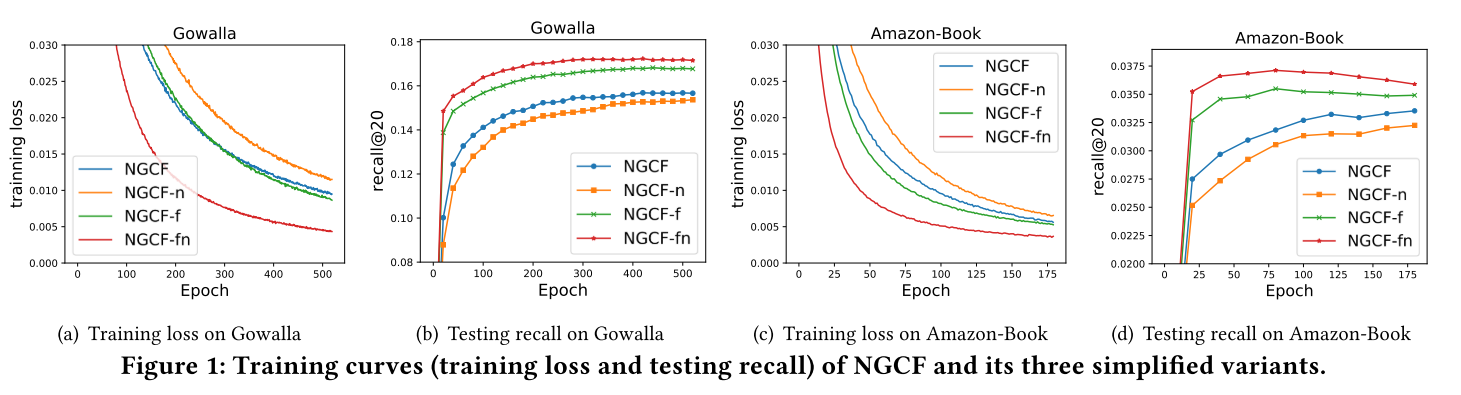
NGCF-f(removes feature transformation)
NGCF-n(removes non-linear activation function)

Finding

(1) Feature transformation imposes negative effect on NGCF
(2) Nonlinear activation affects slightly
(3) Removing them simultaneously improves largely (9.57% relative improvement on recall)
-> Deterioration of NGCF stems from the training difficulty, rather than overfitting

LightGCN

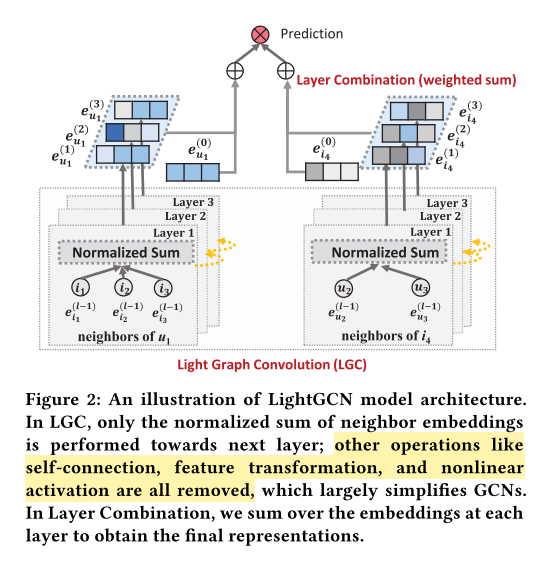
GCN에서 item or user embedding의 기본은 아래와 같음

\bold{e}_{u}^{(k+1)}=AGG(\bold{e}_{u}^{(k)},\left\{\bold{e}_{i}^{(k)}:i\in \mathcal{N}_{u}\right\}).

여기서 self-connction, feature transformation, nonlinear activation을 제거함
따라서, LightGCN에서는 neighborhood aggregation은 아래와 같음

\bold{e}_{u}^{(k+1)}=\sum_{i \in \mathcal{N}_{u}} \frac {1} {\sqrt{\left\vert \mathcal{N}_{u} \right\vert} \sqrt{\left\vert \mathcal{N}_{i} \right\vert}} \bold{e}_{i}^{(k)} \\ \bold{e}_{i}^{(k+1)}=\sum_{i \in \mathcal{N}_{i}} \frac {1} {\sqrt{\left\vert \mathcal{N}_{u} \right\vert} \sqrt{\left\vert \mathcal{N}_{i} \right\vert}} \bold{e}_{u}^{(k)}

Aggregation이 단순 합이므로, trainable model parameter는 0-th layer, $\bold{e}_{u}^{(0)}$ 과 $\bold{e}_{i}^{(0)}$ 에만 존재한다.
Final representation을 얻기 위해서 $K$ 개의 layer를 합하는 layer combination을 수행하는데 이는 아래 수식과 같다.

\bold{e}_{u}=\sum^{K}_{k=0}\alpha_{k}\bold{e}_{u}^{(k)}; \bold{e}_{i}=\sum^{K}_{k=0}\alpha_{k}\bold{e}_{i}^{(k)}

이때 hyperparameter로 지정하는 $\alpha_{k}$ 는 k-th layer embedding의 importance이다.
본 논문에서는 layer마다 동일하게 $1/(K+1)$ 로 설정하는 것이 전반적으로 좋은 성능을 냈다고 한다.
layer combination을 수행한 이유로는 아래의 세 가지 이유를 든다.
(1) 레이어의 수가 증가할수록 over-smoothing되는 문제를 해결하기 위해
(2) 각 레이어의 embedding이 다른 semantic을 포착하기 때문
(3) weighted sum을 이용한 layer combination이 self-connection의 효과를 내기 때문 (uniform한 alpha를 사용한다면서..)

마지막으로 model prediction을 위해 user와 item의 inner product를 수행해 recommendation을 위한 ranking score를 구한다.

\hat{y}_{ui}=\bold{e}_{u}^{T}\bold{e}_{i}

이러한 과정을 matrix form으로 나타내면 아래와 같다.

user-item interaction matrix $\bold{R} \in \mathbb{R}^{M\times N}$ 에 대해

\bold{A}=\begin{pmatrix} \bold{0} & \bold{R} \\ \bold{R}^{T} & \bold{0} \end{pmatrix}, \\

embedding size $T$ 에 대해

\bold{E}^{(0)} \in \mathbb{R}^{(M+N)\times T}, \\

symmetrically normalized matrix $\tilde{A}=\bold{D}^{-\frac{1}{2}}\bold{A}\bold{D}^{-\frac{1}{2}}$ 에 대해

\bold{E}^{(k+1)}=\bold{D}^{-\frac{1}{2}}\bold{A}\bold{D}^{-\frac{1}{2}}\bold{E}^{(k)},

따라서,

\begin{aligned} \bold{E} & = \alpha_{0}\bold{E}^{(0)}+\alpha_{1}\bold{E}^{(1)}+\alpha_{2}\bold{E}^{(2)}+...++\alpha_{K}\bold{E}^{(K)} \\ & =\alpha_{0}\bold{E}^{(0)}+\alpha_{1}\tilde{A}\bold{E}^{(1)}+\alpha_{2}\tilde{A}^{2}\bold{E}^{(2)}+...+\alpha_{K}\tilde{A}^{K}\bold{E}^{(K)} \end{aligned}

sungyeon park

General Engineer

다음 포스트