[코테] 그래프(우선순위 큐) - 배달[프로그래머스]

문제

출처: 프로그래머스 - 배달

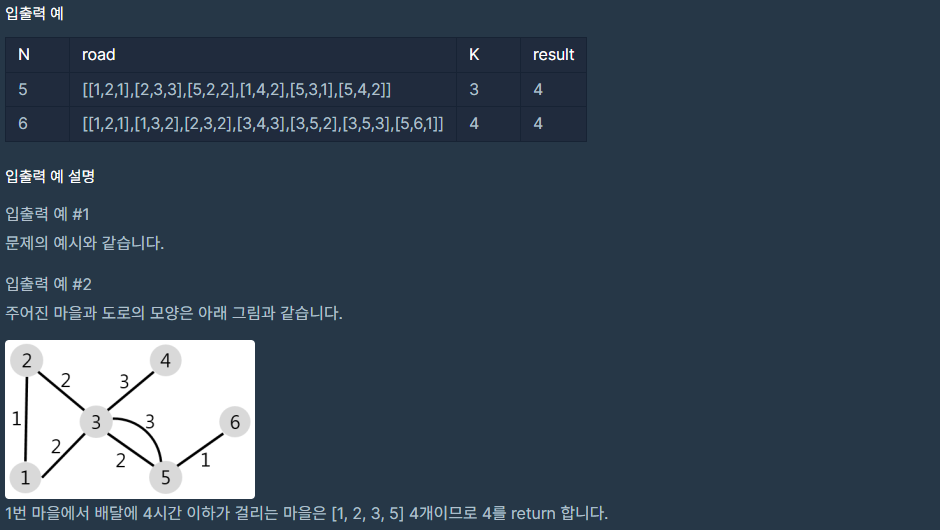
풀이

일명 '그래프' 문제라고 불린다. 주어진 문제의 제시처럼 그래프를 만든 후 '1'번 노드부터 시작해서 다음 노드들을 방문할 때 가중치의 합이 K를 넘지않는 노드의 개수를 찾는 문제다.
시작 노드가 1이기 때문에 1에서 출발을 할 수 있도록 하며, 연결이 되어 있지 않을 수도 있고 노드 '1'에서 다음 노드로 갈 수 있는 노드의 가중치가 K보다 클 수도 있으므로 default 값, 즉 '1'마을은 배달을 할 수 있기에 기본 default 값으로 1을 설정한다.
노드(마을) a에서 b로 갈 때 가중치는 c 로 구성할 그래프를 생성하고, 거리를 담을 수 있는 리스트를 만드는데 그 리스트의 인덱스가 해당 마을 도착 거리가 된다. 해당 노드까지 도착할 수 있는 경우의 수는 여러가지이기에 가장 작은 값을 담을 수 있도록 한다.

풀이 순서를 보면,

1. 그래프를 만든다. 그래프는 1차원 배열로 만들며 행의 인덱스가 바로 출발지점이며 그 안에 그 안의 값중 첫번째가 다음 노드 두 번째가 가중치가 되도록 한다. 모든 거리를 구하는 것이 아닌, 가중치의 값 중 K보다 작은 값의 노드 개수만 구하면 되기에 2차원 배열로 생성할 필요는 없다. 하지만 전체적인 그래프의 구조는 2차원으로 머릿속으로 그려야 한다.
2. 거리 리스트는 노드 개수의 인덱스까지 설정하고(노드개수 + 1) 무한대로 설정하여 가장 작은 값을 업데이트 할 수 있도록 한다. 1번 노드는 자신에게서 자신에게로 가는 경우이기에 0으로 설정하도록 한다.
3. stack을 생성하여 연결되어 있는 노드를 담을 수 있도록 해준다. 이 스택에는 다음 노드와 다음 노드까지 가중치의 합한 것을 넣어준다. 이 때 문제 예시 2번과 같이 값이 여러가지 나올 수 있으며 중복하여 tree에 추가되지 않도록 하기 위해서, 기존의 거리보다 작은 가중치의 값만 업데이트한다.

코드

def solution(N, road, K):
    answer = 1 # 자신의 마을은 배달을 무조건 할 수 있기에, default값은 1로 설정.
    graph = [[] for _ in range(N + 1)]
    for a, b, c in road: # 문제와 같이 양방향 그래프 생성
        graph[a].append([b, c])
        graph[b].append([a, c])

    dist = [1e9] * (N + 1)
    tree = []
    tree.append([1, 0]) # 출발 노드
    dist[1] = 0

    while tree:
        n, ncost = tree.pop()
        for nv, cost in graph[n]:
            if cost + ncost < dist[nv]: # 중복하여 tree에 담지 않도록 기존의 값보다 작은 값을 가질 때만 업데이트 하도록
                dist[nv] = cost + ncost
                tree.append([nv, dist[nv]])

    for i in dist: # K보다 작거나 같은 값만 수를 센다. 그리고 dist[1], 즉 시작 노드의 값은 0이므로 이미 수를 세었기에 빼도록.
        if 0 < i <= K:
            answer += 1