[머신러닝] 선형회귀, 다중선형회귀

📁 선형회귀

<선형회귀 용어 정리>

• 공통
  • Y는 종속 변수, 결과 변수
  • X는 독립 변수, 원인 변수, 설명 변수
• 통계학에서 사용하는 선형회귀 식
  $Y = \beta_0 + \beta_1X + \varepsilon$
  • $\beta_0$: 편향(Bias)
  • $\beta_1$: 회귀 계수
  • $\varepsilon$: 오차(에러), 모델이 설명하지 못하는 Y의 변동성
• 머신러닝/딥러닝에서 사용하는 선형회귀 식
  $Y = wX + b$
  • $w$: 가중치
  • b: 편향(Bias)

📌 결국 두 수식이 전달하려고 하는 의미는 같음

→ 회귀 계수 혹은 가중치를 값을 알면 X가 주어졌을 때 Y를 알 수 있다는 것

📁 회귀분석 평가 지표

<회귀 평가지표 - MSE>

• 에러 정의방법
  • 방법1) 에러 = 실제 데이터 - 예측 데이터 로 정의하기
  • 방법2) 에러를 제곱하여 모두 양수로 만들기, 다 합치기
  • 방법3) 데이터만큼 나누기
• 에러 정의 방법 수식화
  • 방법1) $\varepsilon = y_i - \hat{y_i}$
  • 방법2) $\sum\limits_{i=1}^n (y_i - \hat{y_i})^2$
  • 방법3) $\frac{\sum\limits_{i=1}^n (y_i - \hat{y_i})^2}{n}$

📌 y값의 머리에 있는 ^ 표기를 hat이라고 하며, 예측(혹은 추정)한 수치에 표기

→ 수식 전체를 보면 이해하기 힘들 수 있지만, 단계별로 확인해보면 어렵지 않음

• Mean Squared Erorr(MSE)라고 정의
  $MSE = \frac{\sum\limits_{i=1}^n (y_i - \hat{y_i})^2}{n}$

<선형회귀만의 평가 지표 - R Square>

• 숫자를 예측하는 회귀분석에서 선형회귀에서만 평가되는 지표가 1개 더 있으며, 바로 R Square 지표임

• R Square : 전체 모형에서 회귀선으로 설명할 수 있는 정도

• 어떤 값을 “예측”한다는건 어림짐작으로 평균값보단 예측을 잘해야한다는 것을 의미

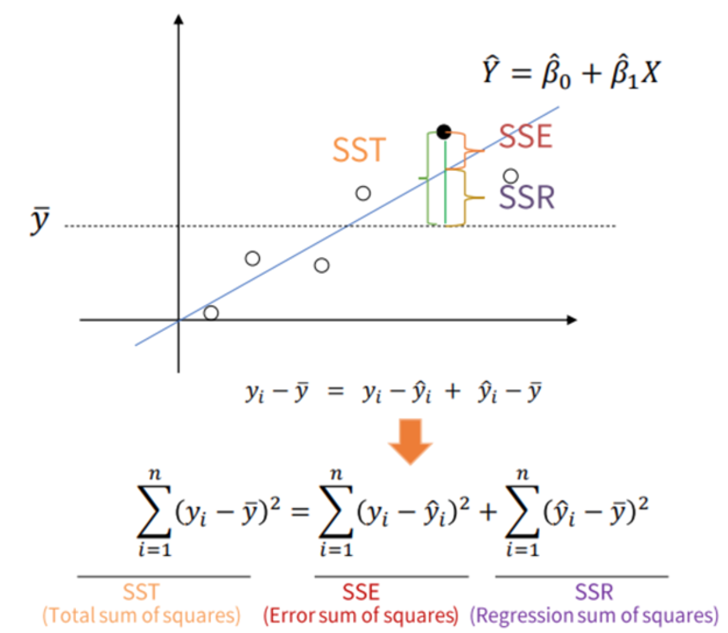
• 기초 용어

  • $y_{i}$: 특정 데이터의 실제 값
  • $\bar{y}$: 평균 값
  • $\hat{y}$: 예측, 추정한 값
    

• R Square의 정의

  $R^2 = \frac{SSR}{SST} = \frac{SSR}{SSR+SSE}$

  

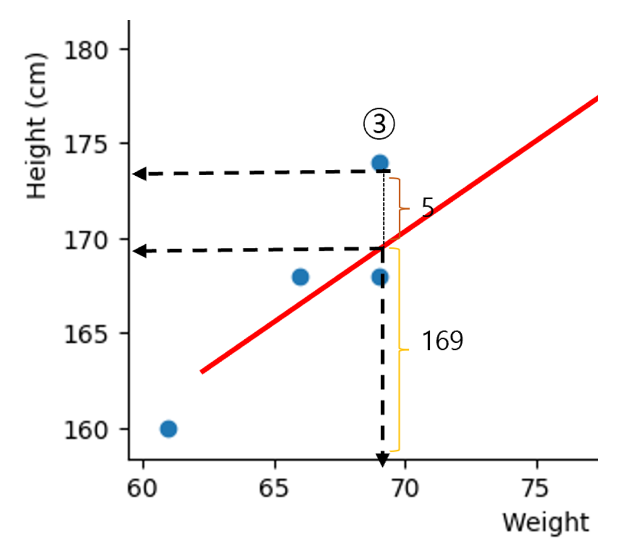
• 3번의 데이터 값은 SST = 174^2, SSR = 169^2

  • 해당 값에 대한 설명력 = 94%
  • 단, 모든 데이터에 대해서 위 계산을 수행

📌 앞으로 만나는 숫자 예측 문제는 모델을 머신러닝이든 딥러닝이든 어떤 모델을 만들어도 위 MSE 지표를 최소화하는 방향으로 진행하고 평가하게 됨

• 기타 평가 지표

  • RMSE: MSE에 Root를 씌워 제곱 된 단위를 다시 맞추기

    $RMSE = \sqrt{\frac{\sum\limits_{i=1}^n (y_i - \hat{y_i})^2}{n}}$

  • MAE: 절대 값을 이용하여 오차 계산하기

    $MAE = \frac{1}{n}\sum\limits_{i=1}^n{\left\vert y_i - \hat{y_i} \right\vert}$

<python 이용시 자주 쓰는 함수>

• sklearn.linear_model.LinearRegression : 선형회귀 모델 클래스
  • coef_ : 회귀 계수
  • intercept : 편향(bias)
  • fit : 데이터 학습
  • predict : 데이터 예측

📁 다중선형회귀

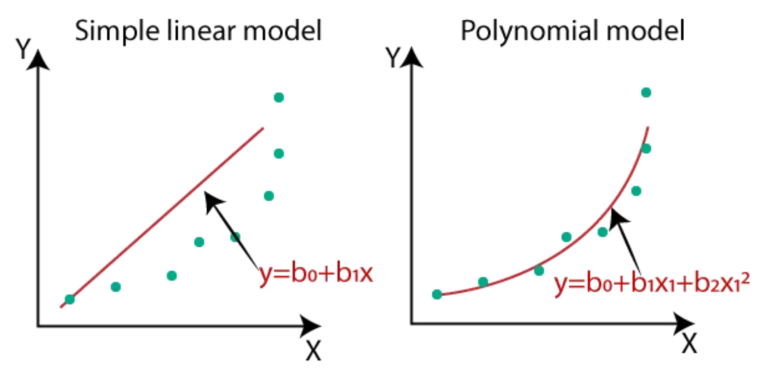
• X와 Y간의 데이터에서 아주 간단한 단순회귀분석만 있는 것이 아니라 실제의 데이터들은 비선형적 관계를 가지는 경우가 많음
• 이를 위해서 X변수를 추가 할 수도, 변형할 수 도 있음

<단순선형회귀 vs 다항회귀>

<수치형 데이터 vs 범주형 데이터>

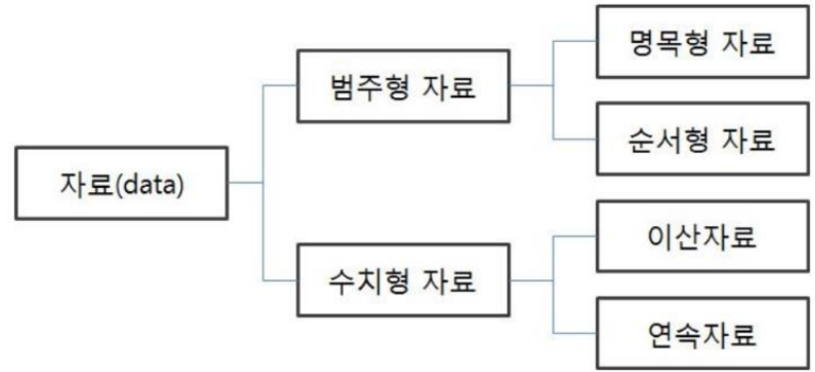
• 수치형 데이터
  • 연속형 데이터 : 두 개의 값이 무한한 개수로 나누어진 데이터 ex) 키, 몸무게
    
  • 이산형 데이터 : 두 개의 값이 유한한 개수로 나누어진 데이터 ex) 주사위 눈, 나이
    
• 범주형 데이터
  • 순서형 자료 : 자료의 순서 의미가 있음 ex) 학점,등급
    
  • 명목형 자료 : 자료의 순서 의미가 없음 ex) 혈액형, 성별

💡 정리

• 머신러닝모델 중에 선형회귀는 이해하기 쉽고 방법도 쉬운 장점이 있지만 말 그대로 X-Y변수간의 선형적 관계가 좋아아만 좋은 성능을 냄
  ↓
  1. 선형성 (Linearity) : 종속 변수(Y)와 독립 변수(X) 간에 선형 관계가 존재해야 함
  
  2. 등분산성 (Homoscedasticity) : 오차의 분산이 모든 수준의 독립 변수에 대해 일정해야 함
  • 즉, 오차가 특정 패턴을 보여서는 안 되며, 독립 변수의 값에 상관없이 일정해야 함
    3. 정규성 (Normality) : 오차 항은 정규 분포를 따라야 함
    4. 독립성 (Independence) : X변수는 서로 독립적이어야 함

<다중공선성 문제>

• 변수가 많아지면 서로 연관이 있는 경우가 많음
• 이처럼 회귀분석에서 독립변수(X)간의 강한 상관관계가 나타나는 것을 다중공선성(Multicolinearity)문제라고 함

<다중공선성 해결방법>

• 서로 상관관계가 높은 변수 중 하나만 선택(산점도 혹은 상관관계 행렬)
• 두 변수를 동시에 설명하는 차원축소(Principle Component Analysis, PCA) 실행하여 변수 1개로 축소

<선형 회귀 정리>

• 장점
  • 직관적이며 이해하기 쉬움(X-Y관계를 정량화 할 수 있음)
  • 모델이 빠르게 학습됨(가중치 계산이 빠름)
• 단점
  • X-Y간의 선형성 가정이 필요
  • 평가지표가 평균(mean)포함 하기에 이상치에 민감
  • 범주형 변수를 인코딩시 정보 손실이 일어남
• Python 패키지
  • sklearn.linear_model.LinearRegression