분할정복법이란?
분할정복법은 주어진 문제를 작은 사례로 나누고 각각의 작은 문제들을 해결하여 정복하는 방법이다.

분할정복법은 문제의 사례를 2개 이상의 더 작은 사례로 나눈다. 이 작은 사례는 주로 원래 문제에서 따온다.
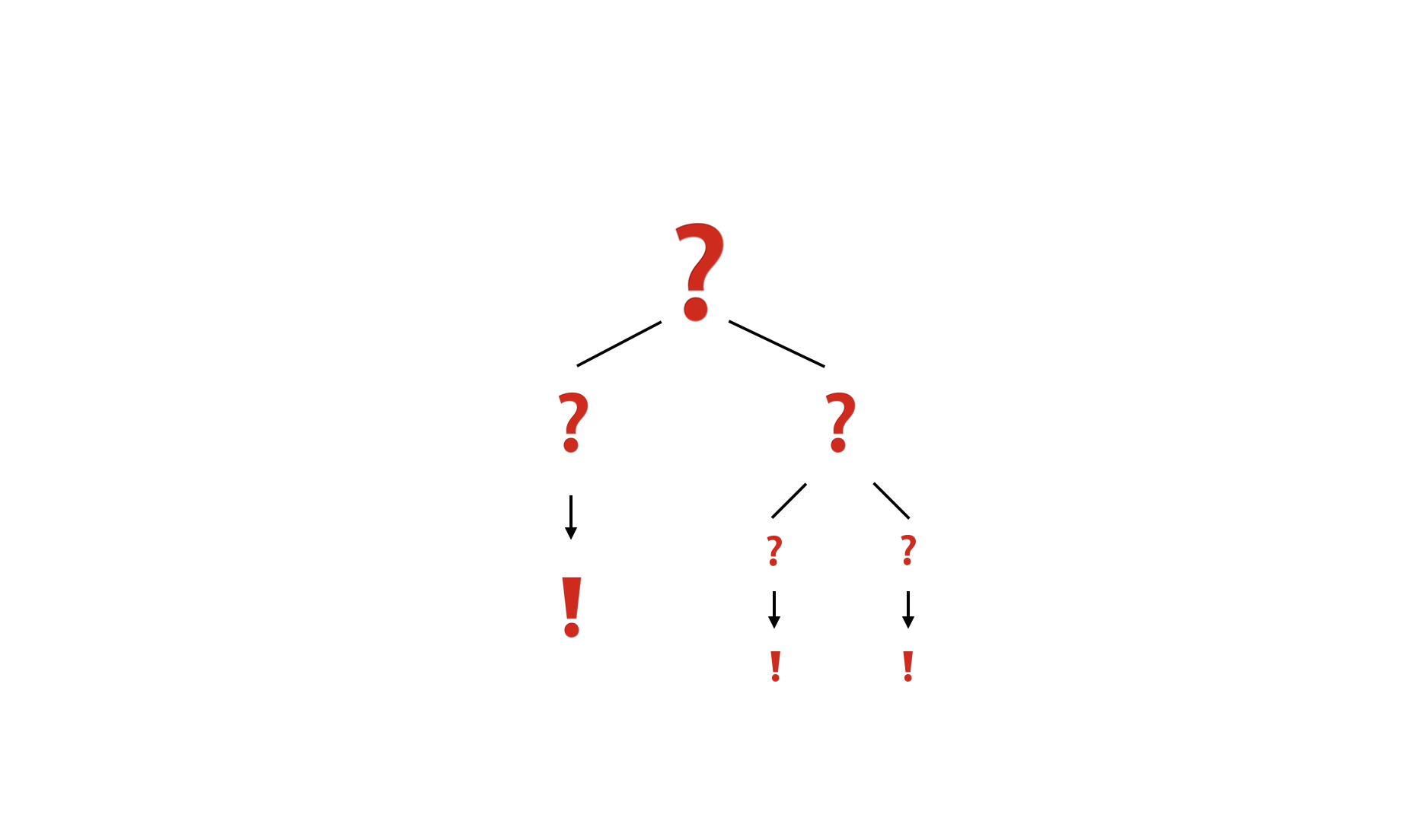
나눈 작은 사례의 해답을 바로 얻을 수 있으면 해를 구하고 아니면 더 작은 사례로 나눈다. 해를 구할 수 있을 만큼 충분히 더 작은 문제로 나누어 해결하는 방법이다.
분할 정복법은 아까 그림으로 봤듯이 하향식 접근 방법으로, 최상위 사례의 해답은 아래로 내려가면서 작은 사례에 대한 해답을 구함으로써 구한다.
분할정복법의 설계전략
그럼 이제 분할정복법을 완전히 정복🤺하기 위해, 분할정복법을 설계전략을 살펴보자.
- 문제를 분할한다.
- 분할한 문제를 각각 해결해 정복한다.
- 필요에 따라 분할한 문제의 답을 통합해 구할 수도 있다.
자세히 살펴보자.
분할정복법의 설계전략은 세 단계로 나눌 수 있다.
먼저 이름 그대로 문제를 하나 이상의 또다른 문제로 분할한다.
그리고 두번째로 그 분할한 문제를 각각 해결하여 정복한다. 여기서 문제가 꼭 두 개로만 나뉘는 것이 아니라, 나뉜 문제에서 또 나뉠 수도 있다. 여기서 재귀, 자기자신을 호출해 하위 작업을 반복적으로 수행하는 재귀를 사용해 문제를 충분히 작게 분할한다. 그리고 분할한 문제를 다 정복했다면 분할정복법은 완료된다.
하지만 필요에 따라서 분할한 사례에 대한 해를 통합해 원래 문제의 해를 구할 수도 있다.
분할정복법은 보통...

분할정복법의 코드 틀을 한번 보자. 먼저 판단한다. 문제가 간단한지, 아닌지 구분해서 문제가 한번에 풀수있는 문제면 그냥 직접 계산해서 문제를 해결한다. 하지만 분할이 필요한 큰 문제라면 문제를 일단 분할한다. 그리고 그 분할한 문제를 호출하여 해결하고 리턴한다. 분할정복법의 코드는 보통 재귀로 자연스럽게 구현된다. 문제를 한번만 분할하는 것이 아닌 충분히 쪼개질 때까지 분할하기 때문이다.
그럼 분할정복법을 더 잘 이해할 수 있도록 예시를 통해 한번 분할정복법을 사용해 문제를 해결해보자.
최댓값 구하기 문제
최댓값 구하기 알고리즘이다. 쉽게 하나하나씩 살펴보도록하자.

6,2,9,8,1,4,17,5 이렇게 배열에 8개의 수가 있다. 이 배열의 수들 중에서 가장 큰 값 하나를 구하고자 한다. 이때 분할정복법을 사용하여 문제를 쉽게 해결할 수 있다.

먼저 배열 안의 수를 8개에서 4개로 분할한다. 아까 분할정복법은 문제를 충분히 작게 분할한다고 했다. 여기서 더 분할할 수 있으니 4개에서 2개로 또 분할한다.

여기서 또 분할할 수 있다. 2개에서 1개로 또 분할한다.

그럼 8개의 수가 다 쪼개져 남아있다. 이제 분할한 문제를 각각 정복한다.

분할한 수를 두개씩 비교하여 더 큰 수만 남긴다.

그리고 남은 그 수 4개를 또 각각 두개씩 비교하여 더 큰 수만 남긴다.

그럼 마지막으로 9와 17, 이렇게 두 짱만 남았다. 이 중 당연히 더 큰 숫자는 17이다.

그러므로 이 최댓값 구하기 문제의 답은 17이 된다.
분할정복법의 장단점
그럼 다음으로 분할정복법의 장단점에 대해 알아보자.
먼저 분할정복법의 장점은 문제를 나눈다는 것이다. 문제를 나눔으로써 어려운 문제를 해결할 수 있다는 특별한 장점이 있다. 그리고 이 방식이 그대로 사용되는 알고리즘도 여럿 있다. 그 예로 최댓값구하기, 쉬트라센 행렬곱셈, 퀵정렬, 이분검색, 합병정렬 등 여러 효율적인 알고리즘에 이 분할정복법이 쓰이기도 한다.
반면 분할정복법의 단점은 함수를 일반적으로 재귀호출한다는 것이 포인트이다. 함수를 재귀적으로 호출하기 때문에 함수 호출로 인한 오버헤드가 발생할 수 있다. 스택에 여러 데이터를 보관하고 있어야 하기 때문에 스택오버플로우가 발생하기도 한다. 스택오버플로우는 프로그램이 실행될 때 입력받는 값이 버퍼를 가득 채워서 버퍼 이후의 공간까지 침범하는 현상, 버그의 일종이라고 할 수 있다. 분할정복법은 이런 스택오버플로우가 발생하거나 과도한 메모리 사용을 할 수도 있는 단점이 있다.
하지만 분할정복법은 꼭 재귀로 구현해야만 하는 것은 아니다. 일반적으로 그럴뿐. 그래서 스택오버플로우가 발생하거나 오버헤드가 발생할 경우 메모이제이션을 사용함으로써 해결한다.
메모이제이션?
메모이제이션은 동일한 계산을 반복해야 할 경우 한 번 계산한 결과를 메모리에 저장해 두었다가 꺼내 씀으로써 중복 계산을 방지할 수 있게 하는 기법이다. 메모리라는 공간 비용을 투입해 계산에 소요되는 시간 비용을 줄이는 방식으로 볼 수 있다.

