오일러 공식
모든 수를 표현 가능하다. complex exponential꼴을 사용하는 이유는 수학적 용이함 때문이다. 그럼 신호처리에서 왜 복소형태를 사용할까? 신호에는 복소 형태가 없다. 하지만 두 개의 신호를 한번에 보낼 때 복소형태가 유리하기 때문에 사용한다.
푸리에 시리즈
테일러 급수가 다항함수를 근사하는 방법이었다면, 푸리에 급수는 주기함수를 근사하는 방법이다. 진동수의 정수배에 해당하는 요소들만 더해도 모든 주기함수를 표현할 수 있다.
내적
내적의 정의이다. a와 b의 내적은 a와 b의 conjugate꼴의 곱의 적분이다(한 주기에 대한).
두 주기함수를 내적해보면 k=r일때만 값이 1이고 나머지는 0임을 알 수 있다.
내적의 결과가 0이라는 것은 orthogonal하다는 뜻이고, 차원이 무한대임을 알 수 있다.
contribution(a_k)찾기
푸리에 급수에 r만큼의 진동하는 주기함수를 내적시켜주면 contribution을 찾을 수 있다.
여기서 contribution의 기하학적 의미는 해당 방향으로의 성분이 얼마나 존재하느냐로 해석가능하다.
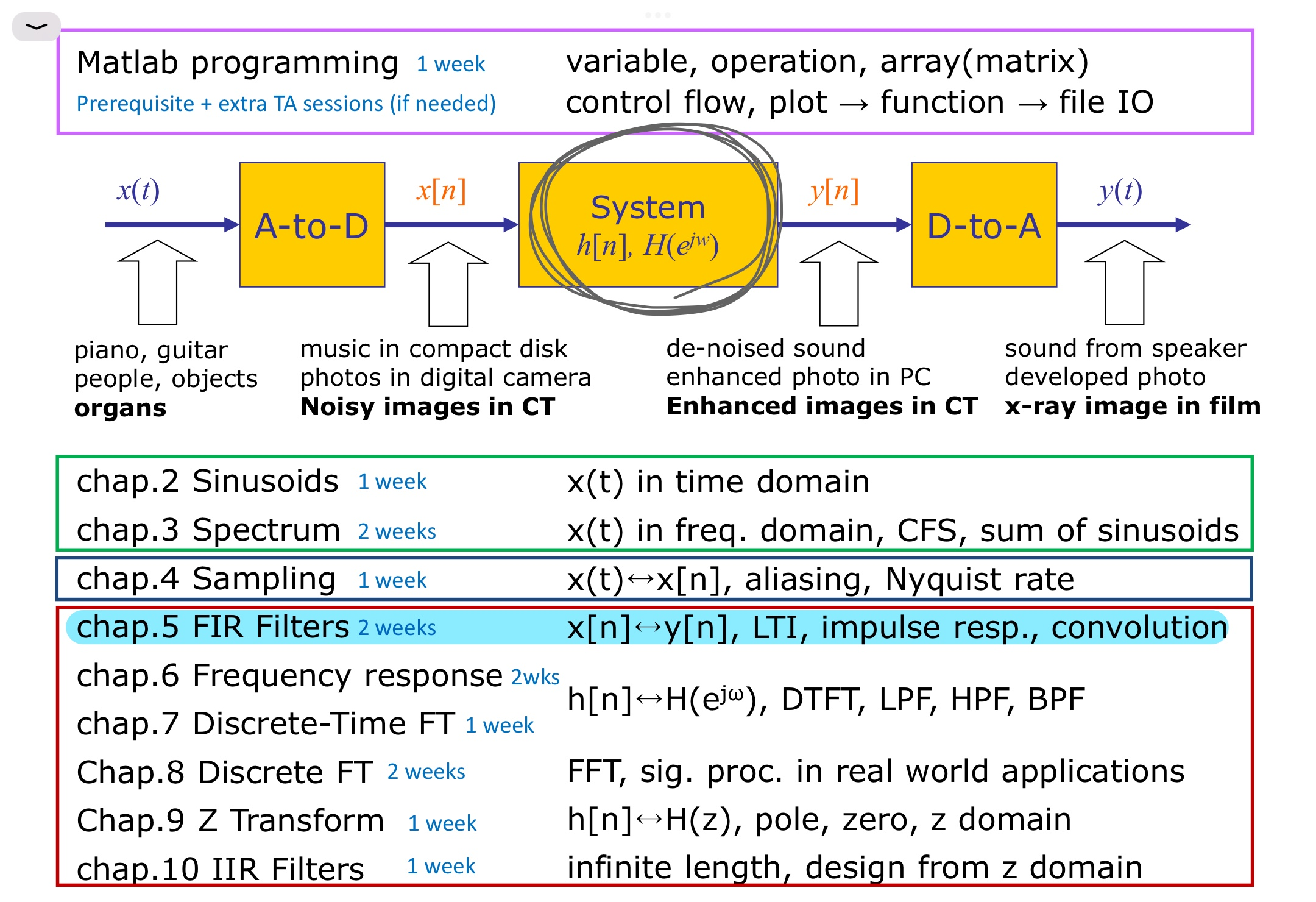
Aliasing(A-to-D)
continuous-time signal에서 충분히 sampling을 하지 못하면 high frequency에 해당하는 부분을 제대로 복원하지 못한다. 위 이미지에서도 울타리부분에서 색 변화가 자주 일어나는 high frequency에 해당하며 제대로 복원되지 못했다. (이는 NeRF논문에서 문제점으로 제기되는 부분이기도 하다.) 이런 현상을 모아레 패턴(Moire) 라고 부른다.
Nyquist Frequency
aliasing을 방지하기 위한 최소한의 sampling frequency이다. 최대 진동수보다 두배이상 큰 sampling frequency를 가져야한다.
LTI(system)
Linear Time-Invariant System의 약자다. Linear하고 Time-Invariant 하다면 이러한 시스템을 LTI시스템이라 부른다. 해당 시스템이 중요한 이유는 예측가능하기 때문이다.
Impulse Response
h(t)를 impulse response라고 부른다. 가장 기본적인 반응이라고 보면 된다. 1만큼의 input을 넣었을 때 나오는 반응이다. 이 반응을 x(t)에 해당하는 횟수만큼 진행한다. 둘을 결합하는 방법이 f이며 convolution이라고 부른다. 아래는 예제이다.
Frequency Response(D-to-A)
위 예제를 계산해보면 알겠지만 convolution은 매우 복잡한 연산이다. 이를 간소화하기 위한 방법이 frequency domain에서 해석하는 것이다. Frequency Response를 X(ejw)에 곱해주기만 하면 convolution을 해결할 수 있다.
또한 시각적인 장점도 있다.
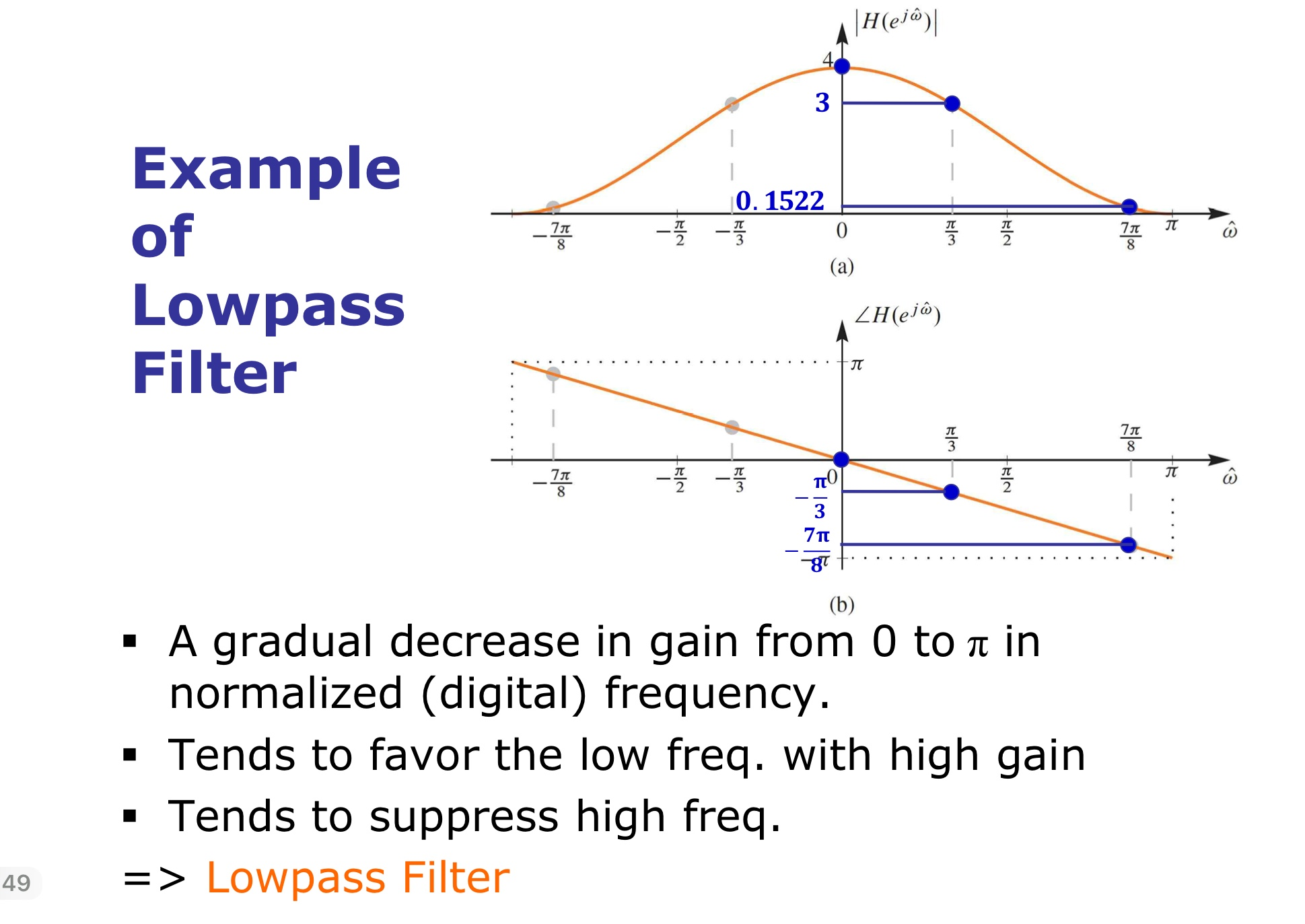
해당 필터가 낮은 주파수를 통과시키는지 높은 주파수를 통과시키는지 알 수 있다. 위 구름에서 magnitude 그래프를 보면 w가 0 부근에서 값이 높으므로 낮은 주파수를 주로 통과시킨다.(LPF)
DTFT
H(ejw)의 일반화다. X(ejw)꼴을 DTFT라고 부르며 (D->C)의 변환 과정이 이루어진다.
DFT
DTFT는 continuous하기 때문에 컴퓨터에서 계산할 수 없다. Discrete한 값들이 필요한데 이를 해결하는 방법이 DFT이다. DFT는 DTFT에서 특정 점들을 가져오는 것이다. (D->D)의 변환 과정이 이루어진다. matlab에서는 DFT보다 빠른 FFT를 사용한다.
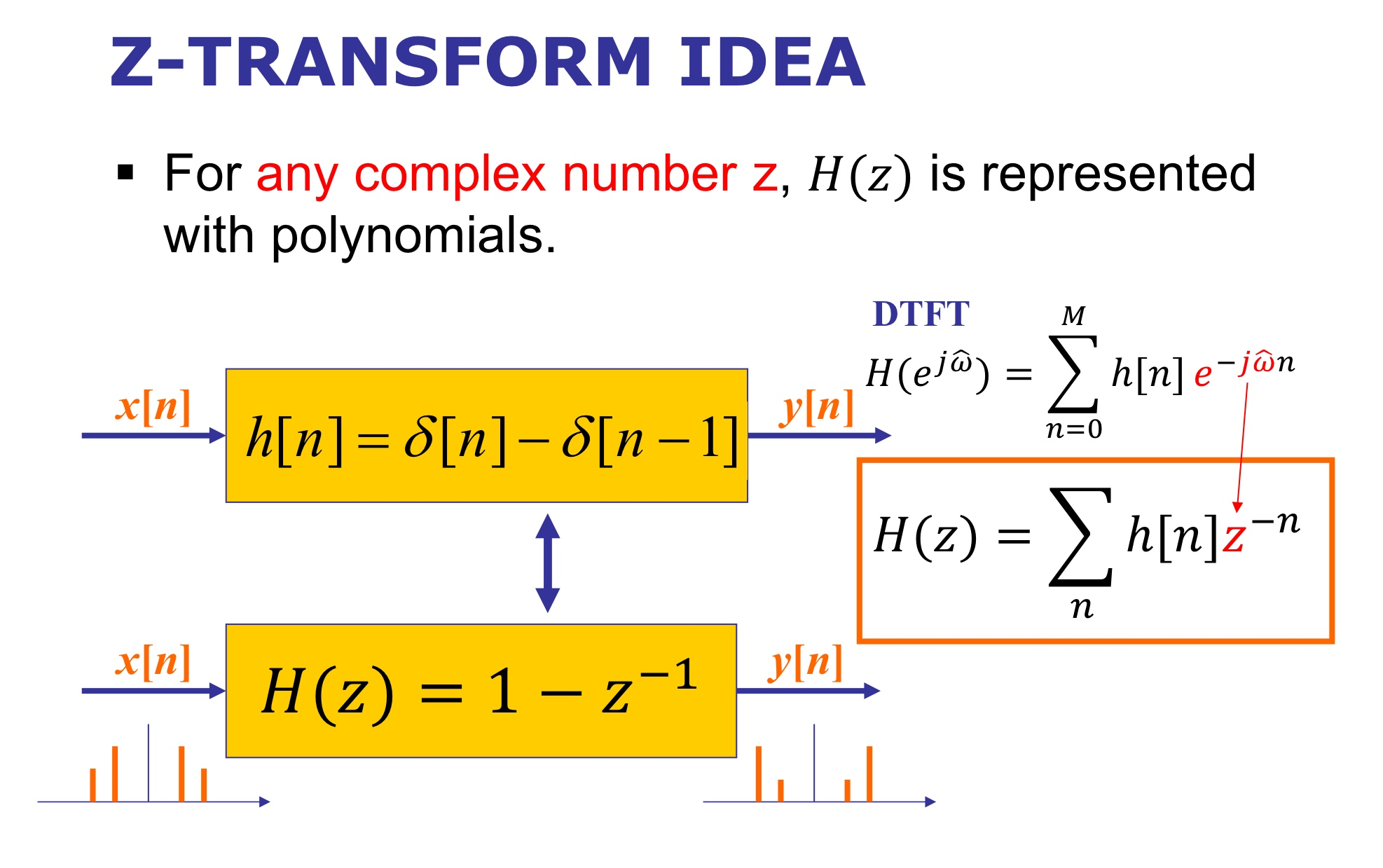
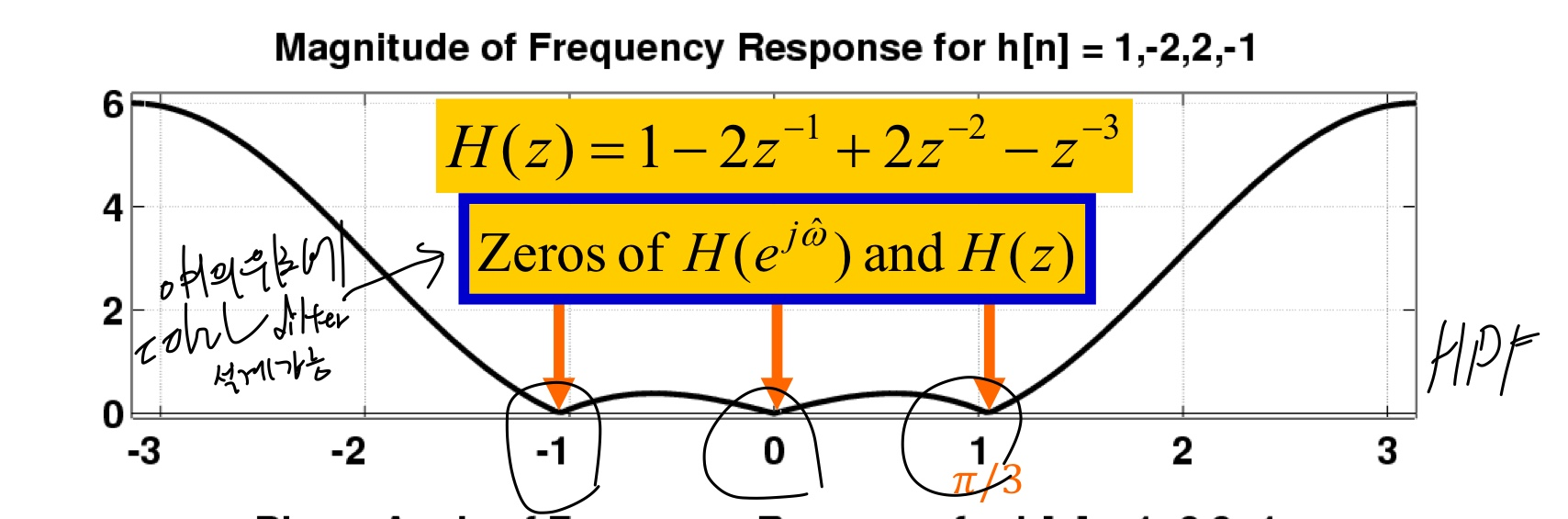
Z-Transform
계산의 편의를 위해 e_jw 대신 z라는 기호를 사용한다. 또한 필터 설계가 더 직관적이라는 장점이 있다.
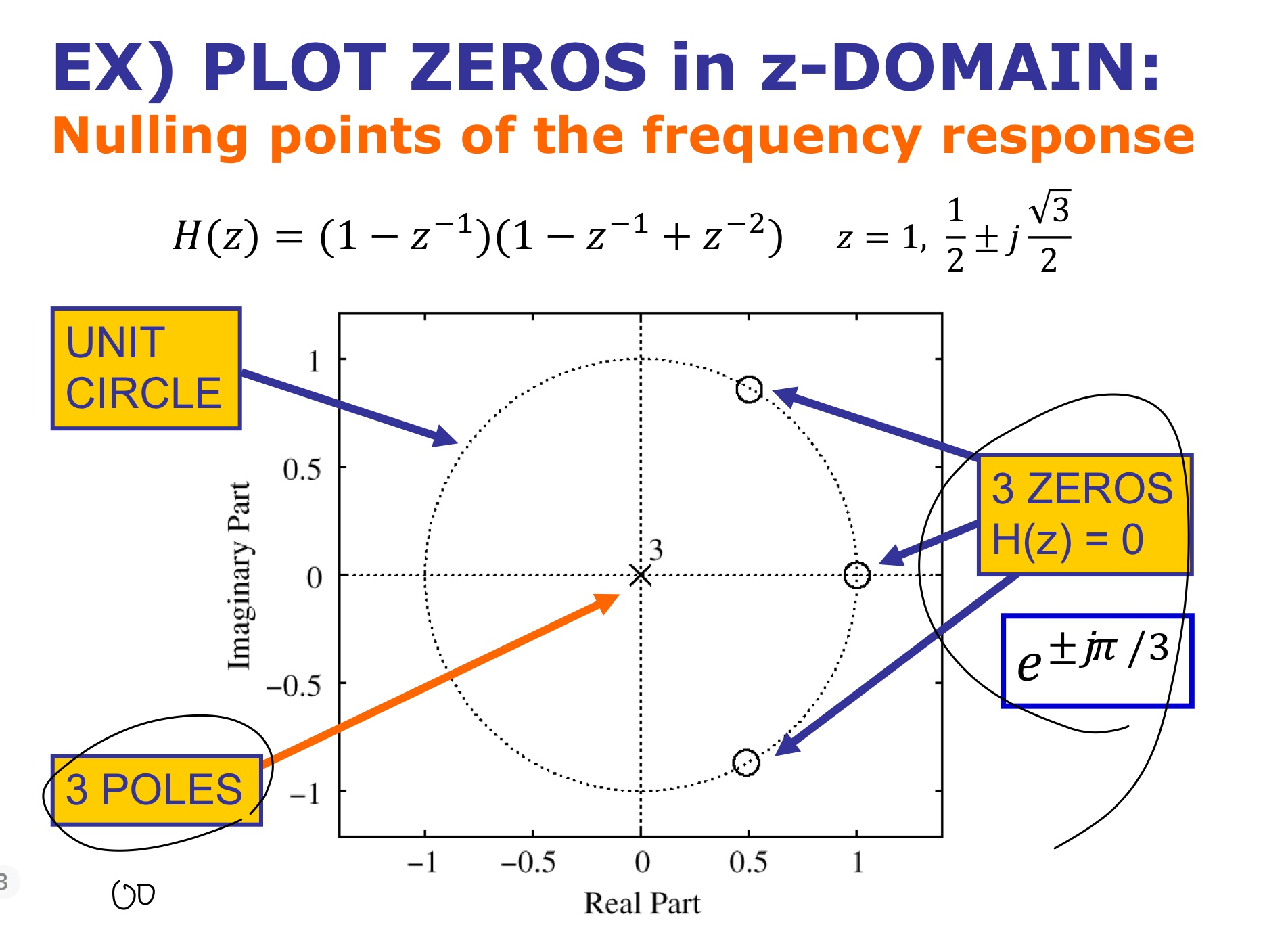
H(z)를 인수분해 하여 zeros와 poles를 찾을 수 있다. 이때 zeros는 nulling point이다.