Reinforcement Learning #1 MDP : Markov Decision Process

1. Markov Property

미래를 오직 현재상태로만 파악하는 것
(미래는 현재상태에 의해서만 결정=과거의 상태와는 무관)

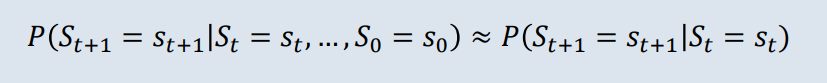
$S_t$ : (현재상태) $S_{t+1}$ : (미래상태) 라고 표기하며,
($S_0, S_1, S_2$~$S_{t-1}$)은 과거상태(history) 일련의 체인을 형성하더라도 영향 받지 않고, $S_t$(현재상태) 스스로에 모든 경우의 수를 포함시켜 하나만을 취급한다.
그렇기에 위와 같은 식이 성립한다.

2. Markov Process

Notation $MP= <S,P>$

State: 현재 시점에서 상황이 어떤지 나타내는 값의 집합
State Space: 가능한 모든 상태의 집합

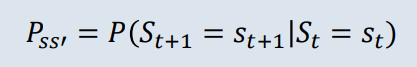
마르코프 과정은 상태 $S_t$(현재상태)에서 $S_{t+1}$(미래상태) 로의 $P$(전이확률)을 나타내는 과정이며, 위와 같은 식이 성립한다.

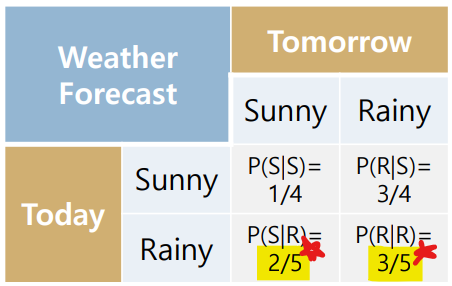
• 전이확률 $P$를 구할 때, 조건부확률(conditional probability)을 사용하는데
  어떤 사건이 일어나는 경우에 다른 사건이 일어날 확률을 말한다.
  (즉, $S_t$(현재상태)가 일어나는 경우에 $S_{t+1}$(미래상태)가 일어날 확률을 말한다)

[주의] FROM ($S_t$(현재상태)) $\to$ TO $S_{t+1}$(미래상태) 순서이지만 Markov process 조건부확률 식을 적을 때 수식은 반대이므로 주의하자!

Example

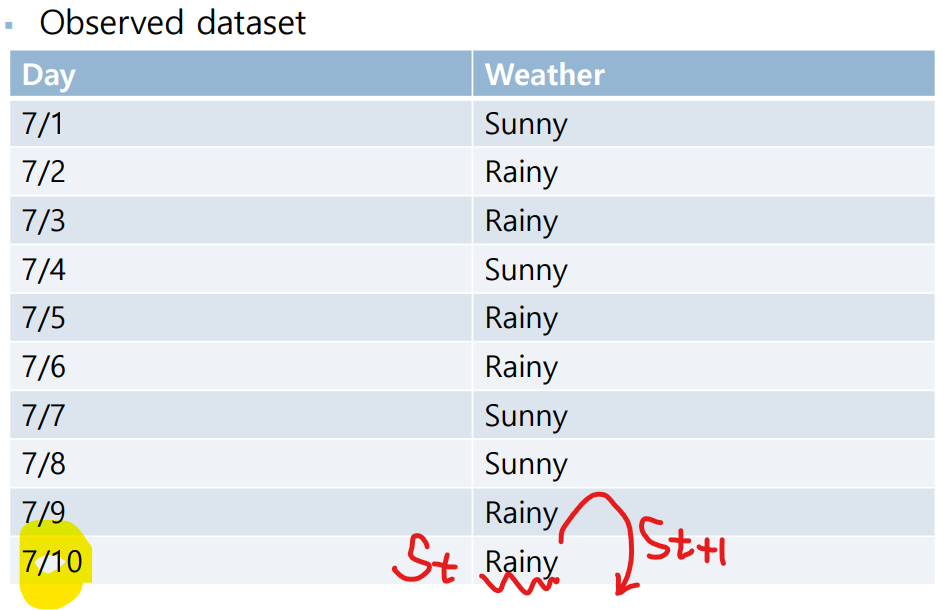
7/1~7/9의 Observed Dataset은 $S_t$(현재상태)와 $S_{t+1}$(미래상태)를 확인할 수 있다.
하지만 7/10의 데이터를 살펴보면 $S_t$(현재상태) : Rainy 는 찾을 수 있지만 $S_{t+1}$(미래상태)의 Dataset이 없다.
그렇기에 7/10의 경우는 제외한 채로 계산하는 것이 맞다.
(아래 표의 노란색 형광펜 경우를 확인하도록 하자)

3. Markov Reward Process | MRP

Notation $MRP= <S,P,R,γ>$

R (reward) : 현재에서 미래상태로 갈 때의 보상(이득)

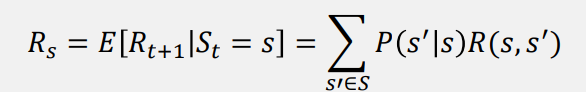
$G_t$ (return) : 보상의 총합(sum of rewards)
γ (discount factor) : $0\leqγ\leq1$

• 아래 $G_t$(return) 공식을 볼 때 γ (discount factor)가 없다면,
  return의 값은 무한대로 발산할 수 있다.
  그렇기에 Markov는 return값이 발산하는 것을 막고 수렴하게 만들기 위해 γ를 사용하였다.
  더불어 γ (discount factor)의 값에 따라, $G_t$(return)이 현재 혹은 미래 보상에 초점 맞추는지 확인할 수 있다.

γ (discount factor) 이 작다면, current rewards
γ (discount factor) 이 크다면, future rewards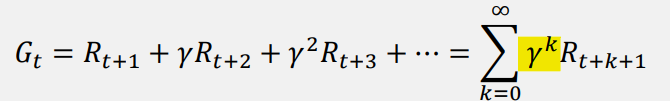

Example

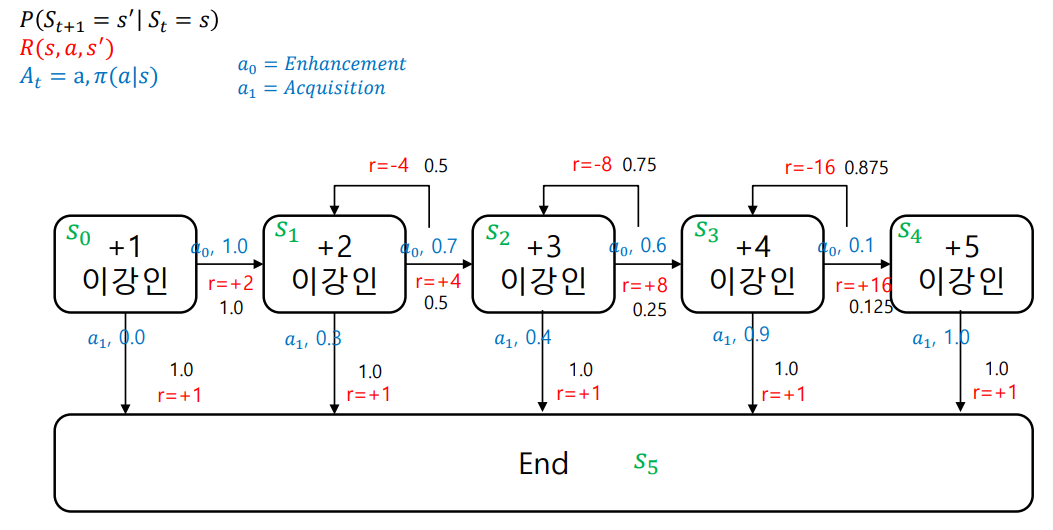
4. Markov Decision Process | MDP

Notation $MDP= <S,A,P,R,γ>$

A (Agent's action) : 가능한 행동의 집합 (set of action)

• 아래 표를 참고하면 MRP에서 행위자인 A(Agent's action)가 추가된 것을 확인할 수 있다.
  Agent는 Environment에서 어떤 행위(action)을 할 지 판단한다.
  
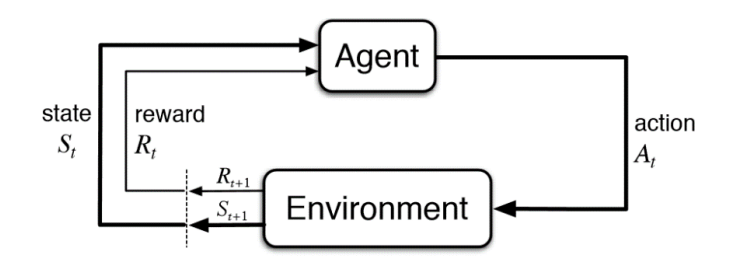
  Policy (π): 모든 단계별 의사결정 모음, 정책 (Probability for Action)
  
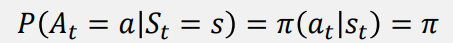
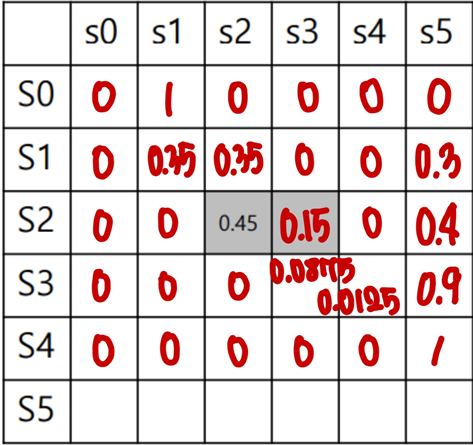
• Policy (π)가 아닌 Action에 대하여 $P$(전이행렬), $R$(reward) 계산할 때의 수식
  
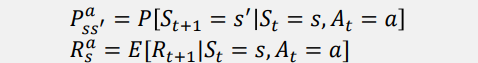
• Policy (π)로 $P$(전이행렬), $R$(reward) 계산할 때의 수식
  

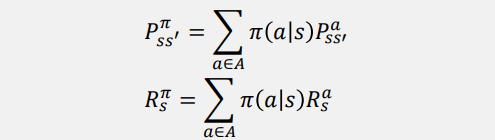
[주의] Policy (π)와 action 자체는 구분할 것. Policy (π)는 모든 단계별 의사결정의 집합이고, action 은 가능한 행동 집합의 원소이다.

5. Deterministic and Stochastic Environment

Deterministic Environment : Episode 가 정해져 있는 경우 (ex.게임)

• $S_t$(현재상태) $\to$ $S_{t+1}$(미래상태)로 가는 $P$(전이확률)이 1.0 or 0.0
  

Stochastic Environment : Episode 가 정해져 있지 않은 경우 (ex. 보통의 인간이 보여주는 경우)

• $S_t$(현재상태)에 똑같은 행동을 해도 $S_{t+1}$(미래상태)에 몇몇의 상태들이 나타나며, $P$(전이확률)은 때에 따라 다르다.

Example

: Stochastic Environment