Bredth-First Search (너비 우선 탐색, BFS)은 상태 공간에서 목표 상대를 찾기 위한 탐색 알고리즘 중 하나로, 탐색 시작 지점에서부터 인접한 상태를 우선적으로 탐색하며, 목표 상태를 찾을 때까지 점진적으로 넓게 확장하는 전략을 따른다. 이 알고리즘은 그래프나 트리 구조에서 가장 가까운 상대부터 찾는데 사용되며, 주로 최단 경로 문제에 적합하다.
너비 우선 탐색은 최단 경로 문제 및 상태 공간 탐색에서 매우 유용하며, 목표 상태의 깊이가 어느 정도 까지 인지 알 수 있는 경우에 특히 효과적이다. 그러나 메모리 사용량이 중요한 경우나 상태 공간이 매우 큰 경우, 다른 탐색 전략을 고려해야 할 수 있다.
특징
- FIFO 큐 (First-In-First-Out Queue) 기반 탐색
- 너비 우선 탐색은 FIFO 큐 자료 구조를 사용하여 상태를 저장하고 탐색한다.
- 초기에 시작 상태를 큐에 넣고, 그 다음에는 큐에서 상태를 하나 씩 빼서 해당 상태의 자식 상태 들을 큐에 추가한다.
- 너비 우선 확장
- 알고리즘은 현재 깊이(depth)에서 가능한 모든 상태를 확장한 후, 다음 깊이로 이동한다.
- 이렇게 하면 현재 깊이에서 가장 가까운 상태부터 점진적으로 탐색 된다.
- 완전성(Completeness) 보장
- 너비 우선 탐색은 무한한 상태 공간이 아니라 한정된 상태 공간에서 사용되는 경우(즉, 상태의 개수가 유한한 경우) 완전성을 가진다.
- 즉, 목표 상태가 존재하는 한, 어떤 경우에도 반드시 목표 상태를 찾아낸다.
- 높은 시간 복잡도(Time Complexity)
- 시간 복잡도는 너비 우선 탐색이 목표상태를 찾는 데 필요한 시간을 나타낸다.
- 시간 복잡도는 상태 공간의 가장 깊은 부분까지 모든 상태를 탐색해야 하므로, O(b^(d+1)) 로 표현된다.
- b = branch, 각 상태에서 이동 가능한 자식 상태의 개수
- d = depth, 최단 경로의 깊이
- 이는 광범위한 탐색 공간에서는 지수적인 시간이 필요함을 의미한다.
- 높은 공간 복잡도(Space Complexity)
- 공간 복잡도는 너비 우선 탐색이 탐색 중에 사용하는 메모리 양을 나타낸다.
- 공간 복잡도는 O(b^(d+1)) 로 표현되며, 모든 가능한 경로의 상태를 메모리에 유지해야 하므로 크게 증가한다.
- 최적성(Optimality) 보장
- 너비 우선 탐색은 단계마다 비용이 동일한 경우에 최적성을 보장한다. 즉, 모든 경로의 비용이 일정하고 같은 경우에 최단 경로를 찾는데 사용할 수 있다.
- 그러나 비용이 다른 경우에는 최적성을 보장하지 않을 수 있다.
Example
- Step 1.
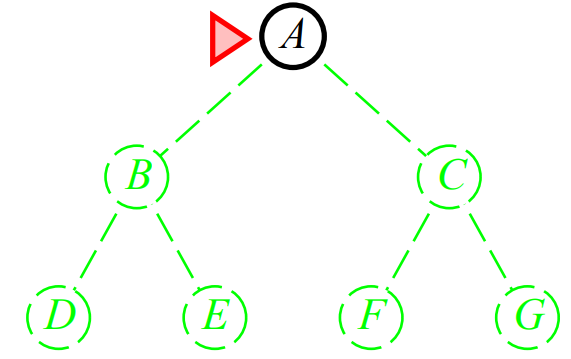
-
Root 노드인 A에서 Search를 시작 (Depth: 0)
-
Step 2.
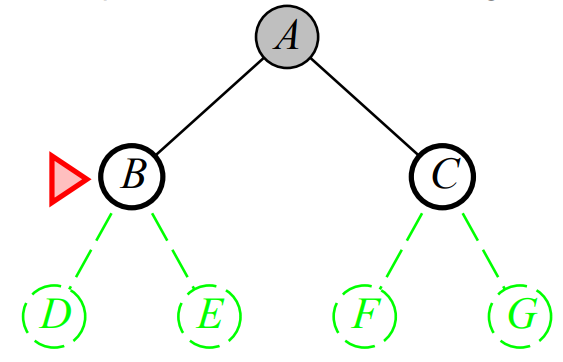
-
A의 Child 노드 중 첫 번째로 B를 탐색 (Depth: 1)
-
Step 3.
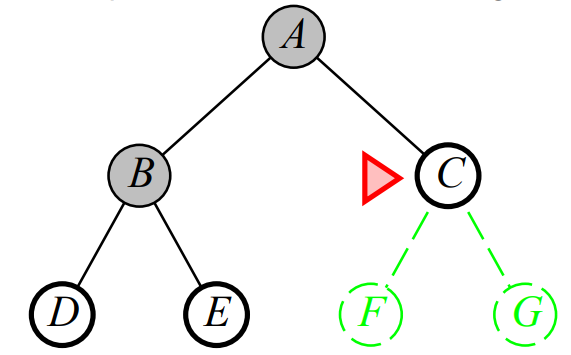
-
그 후 A의 Child 노드 중 두 번째로 C를 탐색 (Depth: 1)
-
Step 4.
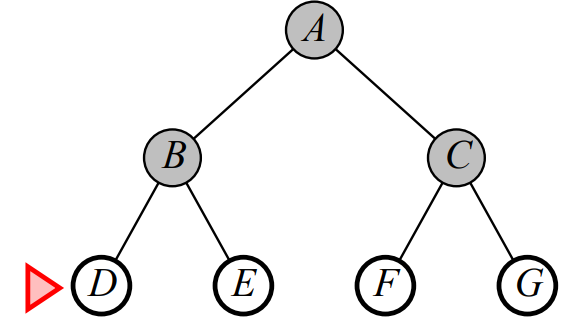
- B의 Child 노드인 D를 탐색 (Depth: 2)
- 이후 D - E - F - G 순서로 노드를 탐색함. (Depth: 2)
단점
- 높은 공간 복잡도 요구
- 높은 시간 복잡도 요구
