Greedy Search (탐욕 알고리즘)은 휴리스틱 함수를 사용하여 각 노드(상태)의 "탐욕스러운" 선택을 수행하는 탐색 알고리즘이다. 이 알고리즘은 목표에 가능한 한 빨리 도달하려는 데 중점을 둔다.
탐욕 알고리즘은 말 그대로 선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 최종적인 해답에 도달하는 방법이다. 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다. 순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택 들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다. 때문에 탐욕 알고리즘은 최적 해를 구하는 데에 사용되는 근사적인 방법이다.

---

조건

• 아래 조건이 성립하지 않는 경우에는 탐욕 알고리즘은 최적해를 구하지 못한다. 그러나 근사 알고리즘으로 사용이 가능할 수 있으며, 대부분의 경우 낮은 시간 복잡도로 인해 실용적으로 사용할 수 있다.

1. 탐욕스러운 선택 조건 (Greedy Choice Property)
   • 앞의 선택이 이후의 선택에 영향을 주지 않는다.
2. 최적 구분 구조 조건 (Optimal SubStructure)
   • 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.

---

문제 해결 과정

1. 선택 절차 (Selection Procedure)
   • 현재 상태에서의 최적의 해답을 선택한다.
2. 적절성 검사 (Feasibility Check)
   • 선택된 해가 문제의 조건을 만족하는지 검사한다.
3. 해답 검사 (Solution Check)
   • 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복한다.

---

특징

1. 목표 중심
   • Greedy Search는 각 단계에서 현재 상태에서 목표에 가장 가까운 상태를 선택하고 확장하는 것을 목표로 한다.
   • 이를 통해 가능한 한 빨리 도달하려는 방식으로 동작한다.
2. 평가 함수 h(n) (휴리스틱)
   • Greedy Search에서 평가 함수 또는 휴리스틱 함수를 사용하여 각 상태의 "유용성"을 평가한다.
   • Greedy Search에서 사용되는 평가 함수(휴리스틱)인 h(n) 은 현재 상태 n 에서 가장 가까운 목표까지의 추정 비용을 나타낸다.
   • 이 평가는 목표에 도달하는 예상 비용 또는 거리를 나타낸다.
     • ex) hSLD(n)
     • hSLD(n) 는 "Straight-Line Distance(직선 거리)" 를 나타내며, 현재 상태 n 에서 목표까지의 직선 거리를 평가하는 휴리스틱 함수이다.
     • 이 휴리스틱 함수는 목표까지의 직선 거리를 사용하여 상태의 가치 또는 유용성을 평가한다.
3. 탐욕스러운 선택
   • 각 단계에서 Greedy Search는 현재 상태에서 가장 높은 평가 또는 가치를 갖는 상태를 선택하고 확장한다.
   • 이 선택은 다음 단계로 진행하기 위한 "탐욕스러운" 결정이다.
4. 최적해(Optimality) 보장 안함
   • Greedy Search는 최적해를 보장하지 않는다.
   • 선택된 상태가 목표까지의 최단 경로가 아닐 수 있다.
   • 이는 Greedy Search가 가장 "탐욕스러운" 선택을 하는 데 초점을 두고, 최적해를 보장하지 않기 때문이다.
5. 완전성(Completemess) 보장 안함

• Greedy Search는 일반적으로 완전성을 보장하지 않는다.
• 무한 루프에 빠질 수 있으며, 특정 경우에는 목표에 도달하지 못할 수 있다.
• 그러나 상태 공간이 유한하고 반복 상태 확인이 수행될 경우에는 완전성을 보장할 수 있다.

6. 평균적 공간 복잡도(Space Complexity)

• Greedy Search의 공간 복잡도는 O(b^m) 이다.
• 이는 모든 노드를 메모리에 유지해야 하기 때문이다.

7. 낮은 시간 복잡도(Time Complexity)
   • Greedy Search의 시간 복잡도는 O(b^m) 이다.
     • b = branch factor, 각 상태에서 확장할 수 있는 후속 상태의 평균 개수
     • m = max depth, 목표 상태까지의 최대 깊이

• 좋은 휴리스틱 함수를 사용할 경우에는 이 시간 복잡도를 크개 개선할 수 있다.

---

Example: Romania

• 다음과 같은 지도가 있을 때 Arad에서 출발하여 Bucharest 까지의 최단 경로를 구하는 문제이다.

• Step 1.

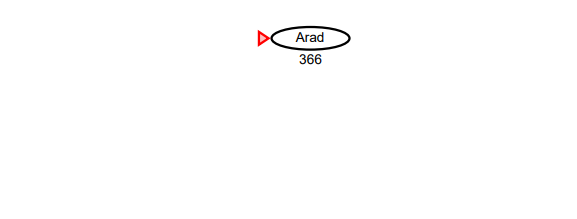
• Arad에서 Bucharest까지의 최단 경로를 구하는 문제이므로 휴리스틱 함수 hSLD(n) = 각 n에서 Bucharest 까지의 직선거리 를 사용한다.

• Arad에서 시작하므로 Arad-Bucharest의 직선 거리인 366을 추가한다.

• Step 2.

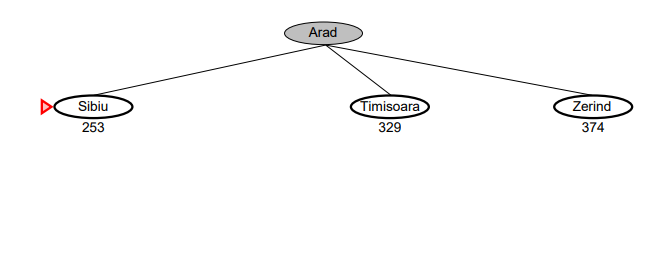
• Arad의 자식 노드인 [Sibiu, Timisoara, Zerind] 를 추가한다.

• 각 도시에서 휴리스틱 함수를 적용하여 Bucharest 까지의 직선 거리를 추가한다. [Sibiu: 253, Timisoara: 329, Zerind: 374]

• 자식 노드 중 휴리스틱 함수의 값이 가장 작은 [Sibiu: 253]으로 확장한다.

• 현재 노드가 Bucharest 인지 검사한다.

• Step 3.

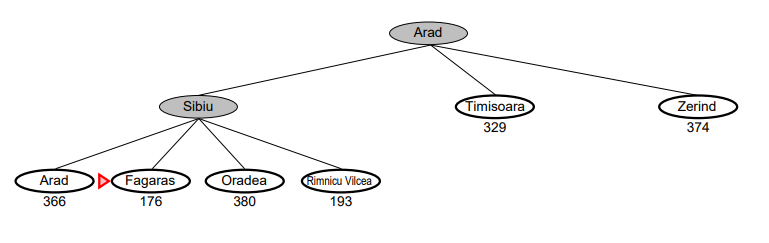
• Sibiu의 자식 노드인 [Arad, Fagaras, Oradea, Rimnicu Vilcea]를 추가한다.

• 각 도시에서 휴리스틱 함수를 적용하여 Bucharest 까지의 직선 거리를 추가한다. [Arad: 366, Fagaras: 176, Oradea: 380, Rimnicu Vilcea: 193]

• 자식 노드 중 휴리스틱 함수의 값이 가장 작은 [Fagaras: 176]으로 확장한다.

• 현재 노드가 Bucharest 인지 검사한다.

• Step 4.

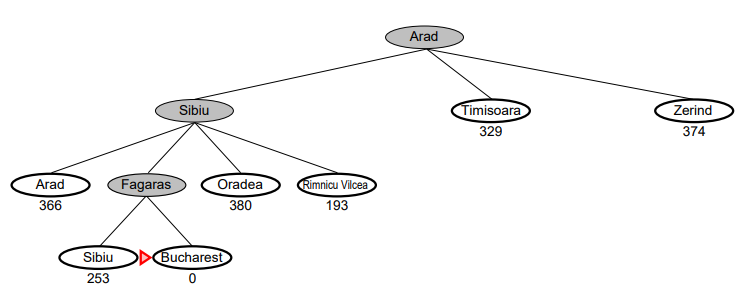
• Fagaras의 자식 노드인 [Sibiu, Bucharest] 를 추가한다.
• 각 도시에서 휴리스틱 함수를 적용하여 Bucharest 까지의 직선 거리를 추가한다. [Sibiu: 253, Bucharest: 0]
• 자식 노드 중 휴리스틱 함수의 값이 가장 작은 [Bucharest: 0]으로 확장한다.
• 현재 노드가 Bucharest 인지 검사한다. 현재 Bucharest에 도착하였으므로 Greedy Search 를 종료한다.

---

Example: 동전 거스름 문제 (매트로이드 문제)

• 한 손님이 계산하는 물건의 가격이 4,040원일 때, 손님이 5,000원을 내밀었다. 이 때 거스름돈은 동전의 개수를 최소한으로 하여 거슬러 줘야 한다.
• 총 거스름돈은 960원이고, 선택할 수 있는 동전 유형은 500원, 100원, 50원, 10원이다.

Greedy Search 적용
1. 선택 절차

• 거스름돈의 동전 개수를 줄이기 위해 현재 가장 가치가 높은 동전을 우선 선택한다.

2. 적절성 검사
   • 1번 과정을 통해 선택된 동전들의 합이 거슬러 준 금액을 초과하는지 검사한다.
   • 초과하면 가장 마지막에 선택한 동전을 삭제하고, 1번으로 돌아가 한 단계 작은 동전을 선택한다.
3. 해답 검사
   • 선택된 동전들의 합이 거슬러 줄 금액과 일치하는지 검사한다.
   • 액수가 부족하면 1번 과정부터 다시 반복한다.

풀이
1. 거스름돈의 500원 1개 추가. [500: 1]
2. 금액을 초과하지 않고 액수가 부족하므로 선택 절차 반복
3. 거스름돈 500원 1개 추가. [500: 2]
4. 금액을 초과하므로 이전 선택을 취소하고 선택 절차로 회귀. [500: 1]
5. 거스름돈 100원 1개 추가. [500: 1, 100: 1]
6. 금액을 초과하지 않고 액수가 부족하므로 선택 절차 반복
7. 거스름돈 100원 1개 추가. [500: 1, 100: 2]
8. 금액을 초과하지 않고 액수가 부족하므로 선택 절차 반복
9. 거스름돈 100원 1개 추가. [500: 1, 100: 3]
10. 금액을 초과하지 않고 액수가 부족하므로 선택 절차 반복
11. 거스름돈 100원 1개 추가. [500: 1, 100: 4]
12. 금액을 초과하지 않고 액수가 부족하므로 선택 절차 반복
13. 거스름돈 100원 1개 추가. [500: 1, 100: 5]
14. 금액을 초과하므로 이전 선택을 취소하고 선택 절차로 회귀. [500: 1, 100: 4]
15. 거스름돈 50원 1개 추가. [500: 1, 100: 4, 50: 1]
16. 금액을 초과하지 않고 액수가 부족하므로 선택 절차 반복
17. 15. 거스름돈 50원 1개 추가. [500: 1, 100: 4, 50: 2]
18. 14. 금액을 초과하므로 이전 선택을 취소하고 선택 절차로 회귀. [500: 1, 100: 4, 50: 1]
19. 거스름돈 10원 1개 추가. [500: 1, 100: 4, 50: 1, 10: 1]
20. 목표 금액이므로 결과를 반환. [500: 1, 100: 4, 50: 1, 10: 1]

• 해당 문제는 탐욕 알고리즘을 적용해도 언제나 최적 해를 구할 수 있는 문제 (매트로이드)이다.