Heuristic (휴리스틱)은 결정 문제나 최적화 문제의 해결에 사용되는 규칙 또는 방법으로, 일반적으로 문제의 복잡성을 감소시키기 위해 사용된다. 휴리스틱은 문제 해결에 관련된 추가 정보나 경험을 기반으로 작성되며, 주어진 문제에 대한 효율적이고 가장 가능성 있는 해결책을 찾는데 도움을 준다.
휴리스틱은 다양한 분야에서 활용되며, 최적화, 경로 탐색, 게임 플레이, 스케줄링, 기계 학습 및 판단 분야에서 유용하게 적용된다. 휴리스틱은 효율적인 문제 해결과 결정에 대한 도구로 널리 사용된다.

---

특성

• 추가 정보 제공
  • 휴리스틱은 주어진 문제에 대한 추가 정보다 지침을 제공한다.
  • 이 정보는 문제 해결을 보다 효과적으로 이끌기 위해 사용된다.
• 경우에 따른 유효성
  • 휴리스틱은 특정 문제 또는 문제 유형에 따라 설계되며, 다양한 문제에 대한 특정 유용성을 갖는다.
  • 휴리스틱은 일반적으로 문제의 도메인 또는 특성에 관련된 정보를 활용한다.
• 정확성 대신 효율성
  • 휴리스틱은 때로 정확성을 희생하고 계산 효율성을 강조한다.
  • 이것은 빠른 결정과 계산적으로 적용 가능한 해결책을 찾는데 도움이 된다.
• 예측 또는 예상 기반
  • 휴리스틱은 예측 또는 예상을 기반으로 작동한다.
  • 휴리스틱 함수는 노드, 상태 또는 경로의 예상 비용, 거리, 가치 등을 평가하는데 사용된다.
• 문제 종속성
  • 각 휴리스틱은 특정 문제나 문제 유형을 해결하기 위해 설계되며, 다양한 문제에 대한 다양한 휴리스틱이 존재한다.
  • 휴리스틱은 문제에 맞게 조정되어야 하며, 다른 문제에 일반적으로 적용되지 않는다.
• 경험 및 도메인 지식 활용
  • 휴리스틱은 종종 도메인 전문가의 경험 및 도메인 지식을 활용한다. 이는 휴리스틱의 설계와 튜닝에 중요한 역할을 한다.
• 탐색 알고리즘과 결합
  • 휴리스틱은 주로 탐색 알고리즘과 결합되어 사용된다.
  • 탐색 알고리즘은 휴리스틱을 활용하여 상태 공간을 효율적으로 탐색하고 결정을 내린다.
• 정확성 보장 안됨
  • 휴리스틱은 정확한 최적해를 보장하지 않을 수 있으며, 부정확하게 설정될 경우 최적해보다 더 좋지 않은 결과를 얻을 수 있다.

---

Consitency (일관성)

휴리스틱 함수 h(n) 가 일관성(Consitency)를 가지려면 다음 조건을 만족해야 한다.

• 특정 상태 n 에서 행동 a 를 통해 다른 상태 n' 으로 이동했을 때, h(n) 과 h(n') 의 값 사이에 다음 부등식이 성립해야 한다.
• h(n) <= c(n, a, n') + h(n')
• 여기서 c(n, a, n') 은 상태 n 에서 상태 n' 으로 이동하는데 필요한 비용이며, h(n) 및 h(n') 은 각각 상태 n 과 n' 에서 목표까지의 휴리스틱 추정 비용이다.
  만약 h 가 일관적 이라면 (일관한 휴리스틱 함수를 사용하면)
• 일관한 휴리스틱 함수를 사용하면, 어떤 상태 n' 에서의 f(n')* 값은 다음과 같이 나타낼 수 있다.
• f(n') = g(n') + h(n')
• 여기서 g(n0) 는 상태 n0 까지의 실제 비용이고, h(n0) 는 휴리스틱 함수를 통해 예측한 목표까지의 추정 비용이다.
  위의 식을 통해 f(n') 을 풀면 다음과 같이 표현할 수 있다.

f(n') = g(n') + h(n')
	  = g(n) + c(n, a, n') + h(n')
	  >= g(n) + h(n)
	  = f(n)

즉, 일관한 휴리스틱 함수를 사용하면, f(n) 값이 어떤 경로를 따라 진행하더라도 높아질 수 있다. 이러한 특성은 A* Search 에서 노드를 확장하는 순서를 결정할 때 중요하며, 최적 경로를 찾는데 도움이 된다.

---

Admissible Heuristics (안정된 휴리스틱)

휴리스틱 함수 h(n) 가 admissible 하다는 것은, h(n) 가 항상 목표 상태까지의 실제 최소 비용보다 크지 않음을 의미한다. 즉 모든 상태 n 에 대해 다음 부등식이 성립한다

• h(n) <= h*(n)

여기서 h(n) 은 휴리스틱 함수를 통해 예측한 상태 n 에서 목표 상태까지의 비용이고, h*(n) 은 실제로 상태 n 에서 목표 상태까지 이르는 최소 비용(최적 비용) 이다.

안정된 휴리스틱 (Admissible Heuristir)의 조건

 1. 가능성 조건 (Consistency Condition)
    모든 상태 n에 대해 휴리스틱 함수 h(n)는 목표까지의 실제 최적 비용인 h*(n)을 과소평가하지 않아야 한다.
    즉, h(n) <= h*(n) 이어야 한다.
 2. 비음수 조건 (Non-Negativity Condition)
    휴리스틱 함수 h(n)은 항상 0 이상이어야 한다.
    즉 h(n) >= 0 이어야 한다.

Example: 8-puzzle

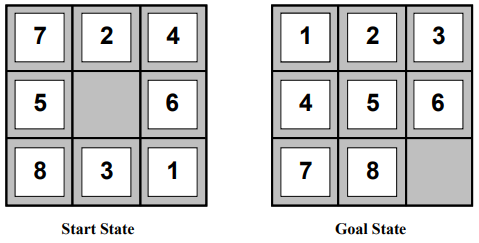
휴리스틱 함수

• h1(n) = number of misplaced tiles, 현재 상태에서 제대로 놓여 있지 않은 타일의 수
• h2(n) = total Manhattan distance, 각 타일이 현재 위치에서 목표 위치까지의 맨해튼 거리를 계산 하고 모두 더한 값

h1(S) = 6. Start State에서 제대로 놓여 있지 않은 타일의 수는 6개 임

h2(S) = 4 + 0 + 3 + 3 + 1 + 0 + 2 + 1 = 14. Start State 에서 각 타일이 현재 위치에서 목표 위치 까지의 맨해튼 거리를 계산하고 모두 더한 값은 14 임

두 개의 휴리스틱 함수 h1(n) 과 h2(n) 이 모든 상태 n 에 대해 Admissible 하며, h2(n) 가 항상 h1(n) 보다 크거나 같은 경우, h2 가 h1 을 "Dominate" 하며, 탐색(Search) 에 있어 더 효과적인 휴리스틱 함수라고 할 수 있다.

• h2(n) 은 h1(n) 보다 더 낮은 경로 비용을 추정하며, 더 정확한 휴리스틱 함수이다.

Type Search Costs
- d is depth of Search Tree

d = 14, IDS(Iterative Deepending Search) = 3,473,941 nodes
	    A*(h1) = 539 nodes
		A*(h2) = 113 nodes
d = 24, IDS = about 54,000,000,000 nodes
		A*(h1) = 39,135 nodes
		A*(h2) = 1,641 nodes

두 개의 admissible 한 휴리스틱 함수 ha(n) 과 hb(n) 이 주어진 경우, 이 두 휴리스틱 함수의 최대값을 취한 휴리스틱 h(n) = max(ha(n), hb(n)) 도 admissible 하며, ha(n) 과 hb(n) 을 모두 "Dominate" 한다.

Given any Admissible Heuristics ha, hb
	h(n) = max(ha(n), hb(n))
is also admissible and dominates ha, hb

즉, 이 휴리스틱은 두 휴리스틱 함수의 상한 경계를 가지며, 두 함수 중 어떤 것보다 낮은 경로 비용을 추정한다. 이것은 휴리스틱 함수를 결합하여 더 정확한 휴리스틱을 만드는데 사용될 수 있음을 의미한다.