다익스트라 알고리즘
1. 가중치 그래프
최단 경로를 구할 때는 가중치 그래프를 사용한다. 가중치 그래프(Weight Graph)는 각 간선 에 연관되는 숫자 레이블(예를 들어 정수)을 로 갖는 그래프이다. 여기서 는 간선 의 가중치(weight)라고 한다.
를 가중치 그래프라고 할 때, 경로 의 길이[length, 또는 가중치(weight)]는 의 간선들의 가중치의 합이다. [1]

2. 다익스트라 알고리즘
다익스트라 알고리즘(영어: Dijkstra Algorithm) 또는 데이스크라 알고리즘은 도로 교통망과 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘 이다. 이 알고리즘은 컴퓨터 과학자 에츠허르 다익스트라(네덜란드어: Edsger Wybe Djkstra)가 1965년에 고안했다. 단일-소스(single-source) 최단 경로 문제에 그리디 메소드를 적용한 결과가 다익스트라 알고리즘이다.
다익스트라 알고리즘의 설명을 간단히 하기 위해 다음을 가정한다. 입력 그래프 는 비항향성이며 단순하다. 즉, 어떠한 자기-반복(self-loop)과 병렬 간선(parallel edges)이 없다. 그러므로 의 간선을 비순서화된 정점들의 쌍 로 표시할 수 있다. 최단 경로를 찾기위한 다익스트라 알고리즘에서, 그리디 메소드의 응용에서 최적화 하려는 비용함수는 최단 경로 거리(shortest path distance)를 계산하는 함수이다.
내에서 에서 로의 거리 근사(approximate)에 사용하기 위해, 내의 각 정점 를 위한 레이블 를 정의한다. 이러한 레이블 는 항상 지금까지 발견한 에서 로의 최상 경로의 길이를 저장한다. 초기에 이고 각 에 대해 이다.
정점들의 선택 집합 를 초기에 공집합 으로 정의한다. 알고리즘의 각 반복에서, 에 들어있지 않으면서 최소의 레이블을 갖는 정점 를 선택하고, 에 를 넣는다. 첫 번째 반복에서는 를 에 넣는다. 에 새로운 정점 가 들어가면 를 경유하여 로 가는 더 좋은 새로운 방법이 있을 지도 모른다는 사실을 반영하기 위해 에 인접하고 에 들어있지 않은 각 정점 의 레이블 를 갱신한다. 이 갱신 연산은 과거의 평가를 취하여 실제 값에 더 가깝도록 하기 위해 향상되어질 수 있는지 점검하기 때문에 경감(relaxation) 절차로 알려져 있다. 다익스트라 알고리즘에 경우, 경감은 간선 를 이용하여 을 위한 더 나은 값이 있는지를 알아보기 위해 의 새로운 값을 계산하도록 간선 에서 실행된다. 간선 경감 연산은 다음과 같이 이루어진다. [1]
3. 다익스트라 알고리즘 예시
다음과 같은 가중치 그래프가 있을 때 에서 까지 갈 때 최단 거리를 구하는 방법은 다음과 같다.
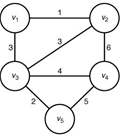
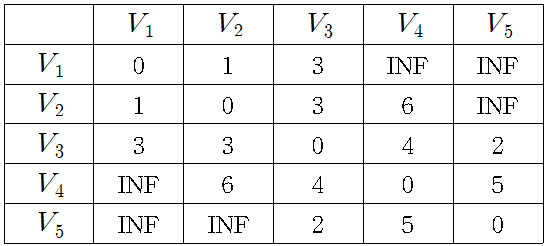
가중치 그래프를 인접 행렬로 나타내면 다음과 같다.
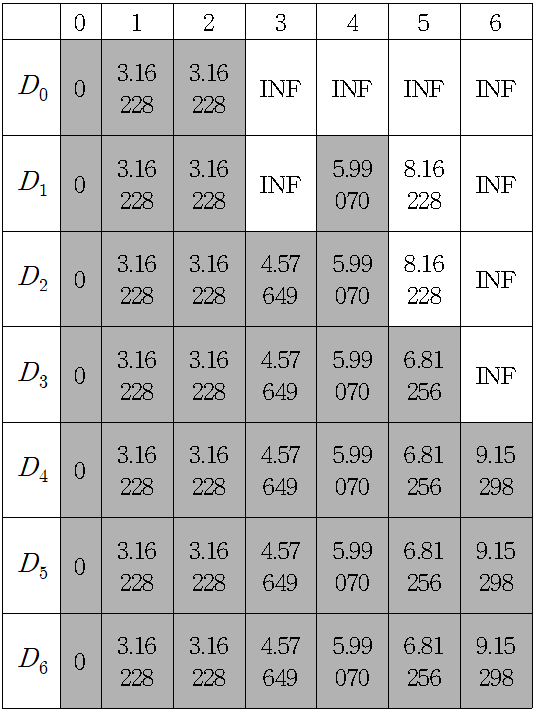
내에서 에서 로의 거리 근사에 사용하기 위해, 내의 각 정점 를 위한 레이블 를 정의하고, 지금까지 발견한 에서 로의 최상 경로의 길이를 저장하여 나타내면 다음과 같이 나타낼 수 있다. 표는 경감 연산을 하여 최단 경로를 저장하여 표시한 값이다.
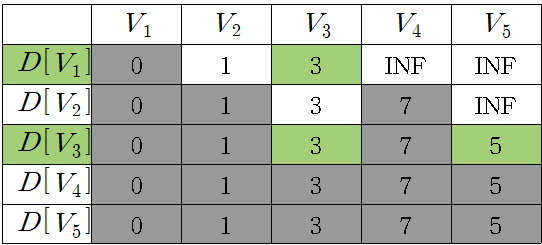
에서 으로 가는 경로는 를 경유하는 방법과 로 바로 가는 방법 2가지가 있다. 이 두 방법의 경로를 비교했을 때 의 경로가 더 짧기 때문에 에서 으로 저장한다. 위와 같은 계산을 하였을 때 에서 출발 할 경우 각 노드에 대한 최단 거리는 표의 최종 값인 이다. 또한 부터 까지의 최종 경로는 이다.
4. 다익스트라 알고리즘의 시간복잡도
다익스트라 알고리즘을 우선순위 큐 의 효율적인 구현인 힙(heap)으로 사용할 경우 실행 시간은 다음과 같다. 우선순위 큐 를 힙(heap)를 사용할 경우 시간 내에 가장 작은 레이블을 가진 정점 를 추출하는 것을 가능하게 한다. 레이블 를 갱신할 때 마다 우선순위 큐 안의 의 키를 갱신하는 것을 필요로 한다. 예를 들어, 만약 가 힙으로 구현되었다면, 이 키 갱신은 기존 키를 먼저 제고하고 새로운 키를 가진 를 삽입함으로써 이루어질 수 있다. 만약 우선순위 가 위치 지시자 패턴(locator pattern)을 지원한다면, 시간의 키 갱신을 쉽게 구현할 수 있다. 의 이러한 구현을 가정한다면 다익스트라 알고리즘은 시간 안에 실행된다. [1][3]
A* 알고리즘
1. A* 알고리즘
A* 알고리즘(영어: A* search algorithm, 발음: A-star)은 최단 경로 탐색 알고리즘 중 하나로 시작 노드와 목적지 노드를 분명하게 지정하여 이 두 노드 간의 최단 경로를 파악한다. 다익스트라 알고리즘에 경우 시작 노드만을 지정해 다른 모든 노드에 대한 최단 경로를 파악하지만, A* 알고리즘의 경우 시작 노드와 목적지 노드를 분명하게 지정하여 이 두 노드 간의 최단 경로를 파악하기 때문에 다익스트라 알고리즘에 비해 실행시간이 짧다. A* 알고리즘은 휴리스틱 추정 값을 통해 알고리즘을 개선한다. 따라서 휴리스틱 추정 값을 어떤 방식으로 제공하느냐에 따라 얼마나 빨리 최단 경로를 파악할 수 있느냐가 결정된다. [4]
이 랑고리즘은 1968년 피터 하트, 닐스 닐슨, 버트램 라팰이 처음 기술하였다. 그 3명의 논문에서, 이 알고리즘은 A알고리즘(algorithm A)이라고 불렸다. 적절한 휴리스틱을 가지고 이 알고리즘을 사용하면 최적(optimal)이 된다. 그러므로 A* 알고리즘이라고 불린다.
A* 알고리즘은 출발 꼭짓점으로부터 목표 꼭짓점까지 최적 경로를 탐색하기 위한 것이다. 이를 위해서는 각각의 꼭짓점에 대한 평가 함수를 정의해야 한다. 이를 위한 평가 함수 은 다음과 같다. [5]
2. A* 알고리즘 예시
다음과 같은 가중치 그래프가 있을 때 노드 에서 노드 까지 가는 최단 경로를 구하는 방법은 다음과 같다. 표의 값은 정확도를 위해 계산 값을 소수점 6째 자리에서 반올림한 값이다.
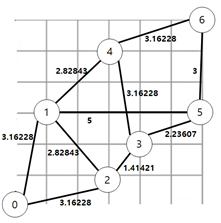
각 노드로부터 도착 노드까지의 유클리드 거리(Euclidean distance)를 휴리스틱 추정 값으로 잡았다. 먼저 열린 목록 저장소(Open List)와 닫힌 목록 저장소(Closed List)를 정의한다. 각각의 저장소에는 Node ID, , , , Parent Node ID가 들어간다. 먼저 닫힌 목록 저장소(이하 )에는 시작 노드를 넣는다. 열린 목록 저장소(이하 )에는 시작 노드와 연결된 노드를 넣는다.
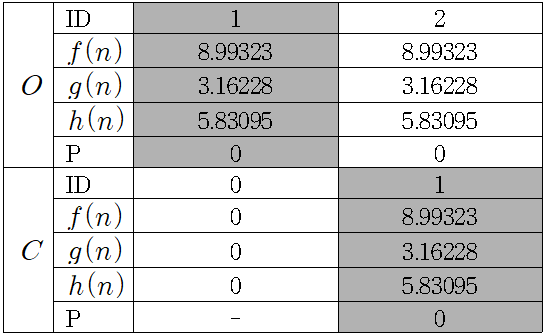
저장소에 들어간 노드 중 이 가장 작은 노드를 선택하여 에 저장소에 저장한다. 다만, 위의 경우처럼 가장 작은 의 값을 가지는 노드가 여러 개일 경우 어느 노드를 선택하여 에 저장해도 상관 없다. 이 경우에는 노드 을 선택하여 저장하였다.
이 가장 작은 노드를 저장소에 저장하였다면, 저장소에 추가된 노드와 연결된 노드 중 저장소에 존재 하지 않는 노드를 저장소에 넣고 계산한다.
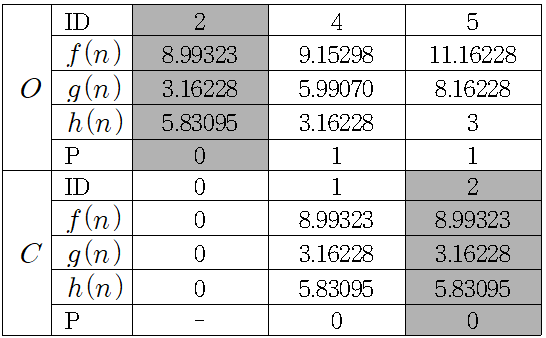
저장소에서 노드 는 노드 이 Parent Node 일 때와 비교 했을 때 노드 이 Parent Node일 때의 이 더 크므로 이 더 작은 Parent Node가 인 노드로 유지한다. 에 저장된 노드 를 비교했을 때 노드 의 이 가장 작으므로 저장소에 넣는다. 그리고 저장소에 노드 와 연결된 노드 중 저장소에 있는 노드를 제외한 노드들을 넣고 계산한다.
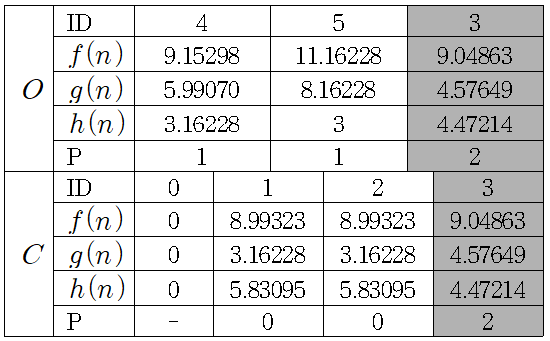
저장소에서 노드 의 이 가장 작으므로 저장소에 넣은 후, 저장소에 노드 과 연결된 노드 중 저장소에 저장되지 않은 노드를 추가하고 계산한다.
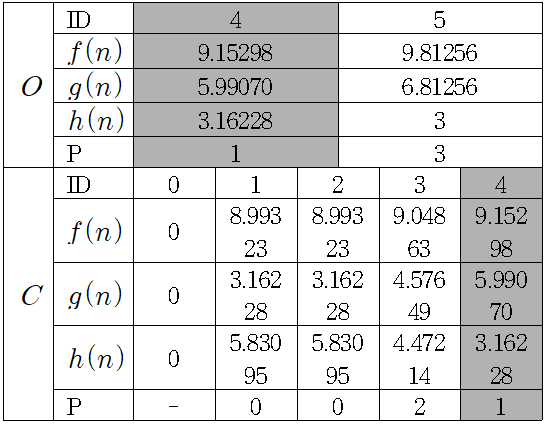
노드 의 경우 Parent Node가 일 때가 Parent Node가 일 때보다 의 값이 더 작으므로 유지한다. 저장소에 저장된 노드 중 크기가 가장 작은 노드 를 저장소에 저장하고, 노드 와 연결된 노드 중 저장소에 존재 하지 않는 노드를 저장소에 넣는다.
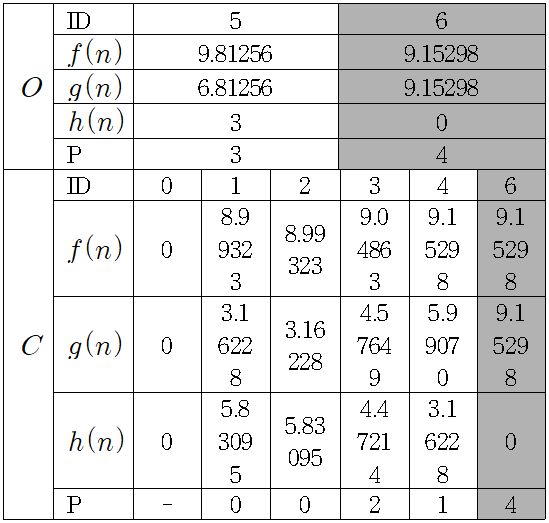
노드 과 노드 은 이미 저장소에 저장되어있으므로 저장소에 새로 추가하지 않는다. 저장소에 저장된 노드 중 노드 의 값이 가장 작으므로 저장소에 추가한다. 도착 노드인 노드 이 저장소에 저장되었으므로 알고리즘은 종료된다. 이제 도착 노드의 Parent Node를 보며 시작 노드까지 거슬러 올라가면 임을 알 수 있다. 따라서 순의 경로가 최단 경로이며, 최단 거리는 약 9.15298 이다.
3. A* 알고리즘과 다익스트라 알고리즘의 차이
A* 알고리즘과 다익스트라 알고리즘의 가장 큰 차이는 도착 노드가 정해져 있냐 정해져 있지 않냐 이다. A* 알고리즘의 경우 시작 노드와 도착 노드 모두가 정해져 있기 때문에 도착 노드에 도달하는 최단 경로만을 구한다. 반면 다익스트라 알고리즘의 경우 도착 노드가 정해져 있지 않기 때문에 시작 노드로부터 모든 노드에 대해 최단 경로를 구하는 방법이다. 따라서 A* 알고리즘의 실행시간이 다익스트라 알고리즘의 실행시간보다 짧다. 그래서 일반적으로 A* 알고리즘을 게임 내에서 길 찾기 알고리즘으로 사용하는 경우가 많다.
A* 알고리즘의 경우 휴리스틱 추정 값에 많이 의존한다. 따라서 휴리스틱 추정 값에 따라서 최단 경로가 아닐 수도 있다. 예를 들어 위의 예시에서 휴리스틱 추정 값을 유클리드 거리(Euclidean distance)를 썼는데, 휴리스틱 추정 값으로 유클리드 거리가 아닌 맨해튼 거리(Manhattan distance)를 쓸 경우 다음과 같은 결과가 나온다.
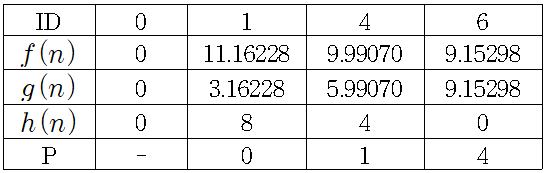
위 표의 값은 첫 번째 저장소에서 노드 과 노드 에 값이 같았을 때 노드 을 저장소에 넣은 결과 이다. 그러나 노드 이 아닌 노드 를 저장소에 넣을 경우 다음과 같은 결과가 나온다.
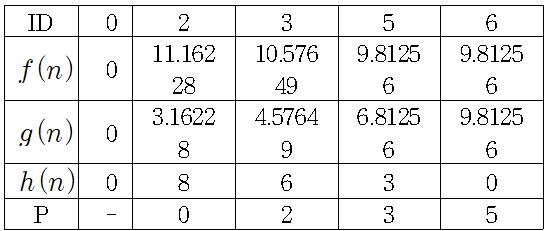
노드 을 처음 저장소에 넣었을 때와 다르게 최종 경로가 달라진다. 이는 A* 알고리즘으로 최단 경로를 구하고 싶다면 위 가중치 그래프에서는 맨해튼 거리가 휴리스틱 추정 값으로 알맞지 않음을 알 수 있게 한다.
또한 A* 알고리즘에서 휴리스틱 추정 값을 적용하지 않을 경우, 즉 일 경우 A* 알고리즘은 다익스트라 알고리즘과 동일하게 모든 노드에 대해 계산하게 된다.
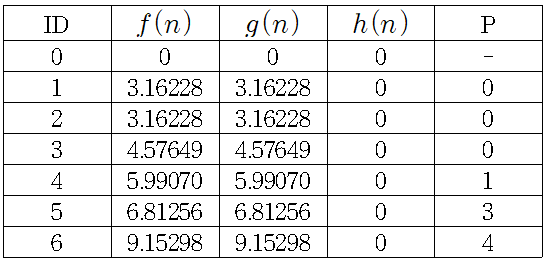
참고문헌
- [1] Michael T.Goodrich, Roberto Tamassia, David Mount. Data Structures and Algorithms in C++. Trans. 범한서적주식회사, 2004
- [2] 이승찬. 컴퓨팅 사고를 위한 기초 알고리즘 모두의 알고리즘 with 파이썬, 길벗, 2017
- [3] “데이크스트라 알고리즘”, 위키백과, 2019년 10월 25일 수정, 2019년 12월 4일 접속, https://ko.wikipedia.org/wiki/%EB%8D%B0%EC%9D%B4%ED%81%AC%EC%8A%A4%ED%8A%B8%EB%9D%BC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
- [4] “최단 경로 탐색-A*알고리즘”, GIS DEVELOPER, 2018년 6월 21일 수정, 2019년 12월 5일 접속, http://www.gisdeveloper.co.kr/?p=3897
- [5] “A 알고리즘”, 위키백과, 2019년 12월 5일 접속, https://ko.wikipedia.org/wiki/A_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
- [6] “PathFinding”, Github, 2019년 12월 6일 접속 https://qiao.github.io/PathFinding.js/visual/
본 문서는 2019-2학기 세종대학교 디지털 게임의 이해 소논문 [길 찾기 알고리즘과 미로에서 최적화 할 수 있는 방안, 세종대학교, 소프트웨어학과, 19011625, 허진수] 중 일부 내용을 velog에 맞춰 정리한 글입니다. 원문은 아래 링크에서 확인할 수 있습니다.
