논문 리뷰_SHAP value

논문 : A unified Approach to Interpreting Model Predictions

• 읽기: 21.07.06~21.07.07

• 이해가 부족한 부분이 있을 수 있습니다. 틀린 부분 있으면 언제든 댓글로 남겨주세요.

1. Introduction

예측 모델의 결과에 대해 올바르게 해석하는 것은 굉장히 중요하다.
linear model 같은 간단한 모델들은 계수를 이용하여 결과에 대한 명확한 해석이 가능하나, 예측력이 높지 않다는 단점이 있다. (데이터에 따라 다름)
그에 반해 머신러닝, 딥러닝 모델은 비선형적인 방법으로 예측력 높은 결과를 도출한다는 아주 큰 장점에 비해, 어떤 과정을 통해 그러한 결과를 도출했는지 알 수 없어 'black box'라 불리기도 한다.
예측력이 좋은 복잡한 모델들을 실제에 적용하기 위해서는 그 결과가 해석 가능해야한다. 하지만, 아직 명쾌하게 해석하는 방법들은 부족한 실정이다.

이 논문에서는 'explanation model' 개념을 도입하여 복잡한 모델이 도출한 결과에 대해 해석하는 방법들을 소개해보고자 한다.

아래는 수식과 개념 위주로 설명하겠다.

2. Additive Feature Attribution Methods

• Notation

$f$ : The original Prediction model to be explained
$g$ : The explanation model

$x$ : single input
$x=h_{x}(x')$, $x'$: simplified inputs
$g(z')\approx f(h_{x}(z'))$

$\implies$ mapping function $h_{x}(x')$를 사용하여 $x$를 변환한 뒤, explanation model에 대입한다. 이 값은 평가되는 값들에 따라서 의미가 달라진다.

* Definition 1: Additive feature attribution methods

$g(z') = \phi_{0}+\sum_{i=1}^{M} \phi_{i}z_{i}'$

$z'\in\{0,1\}^{M}$, $M$: The number of simplified input features.
$\phi_{i} \in R$

2-1. LIME (Locally Interpretable Model-agnostic Explanation)

• LIME: 데이터를 가까이서 보면 선형 관계가 존재할 것이라 생각하고, 그를 기반으로 모델의 결과를 해석 하는 것.

• mapping 결과 생성된 $x'$는 binary이다. 기존의 $x$가 어떤 종류의 데이터인지에 따라 binary 값의 의미가 다름.

• image인 경우 1: leaving the super pixel as its original value / 0: replacing the super pixel with an average of neighboring pixels

• 기여도 $\phi$를 찾기 위해서, LIME은 아래의 식을 최소화시킨다.
  $\xi= \argmin_{g \in G} L(f,g,\pi_{x'})+\Omega(g)$.
  $L$: squared loss
  $\implies$ Penalized Linear Regression

• $x'$도 binary이고, penalized linear regression을 최적화 시키는 건 그렇게 어려운 일은 아니므로 이전의 복잡한 모델을 해석하는 것보다는 더 쉽겠지!

• LIME은 "Why Should I Trust You: Explaining the Predictions of Any Classifier" 논문 리뷰에서 더 자세히 다룰 예정 :)

2-2. DeepLIFT

• "summation-to-delta"

$\sum_{i=1}^{n} C_{\Delta x_{i} \Delta o}=\Delta o$,
$\Delta o=f(x)-f(r), \Delta x_{i}=x_{i}-r_{i}$, $r$: reference input

$\phi_{i}=C_{\Delta x_{i} \Delta o}, \phi_{0}=f(r)$이면 definition 1의 식과 같아진다.

• mapping $x=h_{x}(x')$
  $x'=1$ : original value
  $x'=0$ : reference value

2-3. Layer-wise Relevance Propagation

• DeepLIFT와 동일
• mapping $x=h_{x}(x')$
  $x'=1$ : original value
  $x'=0$ : An input

2-4. Classic Shapley value Estimation

1) Shapley regression values
: feature importance for linear model in Multicollinearity

• weighted average of all possible differences

$\phi_{i} = \sum_{S\subseteq F\{i\}} \frac{|S|!(|F|-|S|-1)!}{|F|!} [f_{S \cup \{i\}}(x_{S \cup \{i\}})-f_{s}(x_{s})]$

$F$: All Features, $S$: subset
$f_{S \cup \{i\}}$: trained with that feature present
$f_{s}$: trained with the feature withheld

original $x \to h_{x} \to 1$: the input is included in the model
original $x \to h_{x} \to 0$: exclusion from the model

• $\phi_{0}=f_{\phi}(\phi)$라 하면, definition 1의 식과 같아진다.

2) Shapley Sampling values

• explain any model by

1. 위의 식에 sampling approximation을 적용
2. train data로부터 sampling한 데이터와 결합시킴으로써 모델로부터 하나의 변수를 제거하는 효과에 접근. $\implies$ 계산량을 줄일 수 있다.

3) Quantitative input influence

• Shapley Sampling values와 비슷

3. Simple Properties Uniquely Determine Additive Feature Attributions

• 논문에서 가장 중요한 척추 역할.(내 생각)
• 소개되는 여러 방법들이 이 성질들을 만족해야만 한다.

1. Local Accuracy

$f(x)=g(x')=\phi_{0}+\sum_{i=1}^{M} \phi_{i} x_{i}'$
$x=h_{x} (x')$, $f$ : original model, $g$ : explanation model
where $\phi_{0}=f(h_{x}(0))$

2. Missingness

$x_{i}'=0 \implies \phi_{i}=0$

• 모델에 포함되어있지 않으면 attribution도 없다.

original $x \to h_{x} \to 1$: 모델에 존재
original $x \to h_{x} \to 0$: 모델에 존재 x

3. Consistency

Let $f_{x}(z')=f(h_{x}(z))$ and $z' \backslash i$ denote $z_{i}'=0$

For any two models $f$, $f'$,
$f_{x}'(z')-f_{x}'(z' \backslash i) \ge f_{x}(z')-f_{x}(z' \backslash i)$이면,

$z'\in\{0,1\}^{M}$에 대하여 $\phi_{i}(f',x) \ge \phi_{i}(f,x)$이다.

* Theorem 1: 단 하나의 explanation model g가 definition 1을 따르며, 위의 3가지 특성을 모두 만족한다.

$\phi_{i}(f, x) = \sum_{z'\subseteq x'} \frac{|z'|!(M-|z'|-1)!}{M!} [f_{x}(z')-f_{x}(z' \backslash i)]$

where
$|z'|$ : the number of non-zero entries in $z'$

4. SHAP (SHapley Additive exPlanation) Values

• Feature Importance를 구하는 척도
• 앞에서 적은 Theorem의 solution.

$f_{x}(z')=f(h_{x}(z'))=E[f(z)|z_{S}]$
$S$: the set of non-zero indexes in $z'$

1-3 성질 모두 만족해야하고, conditional expectation 사용한다.

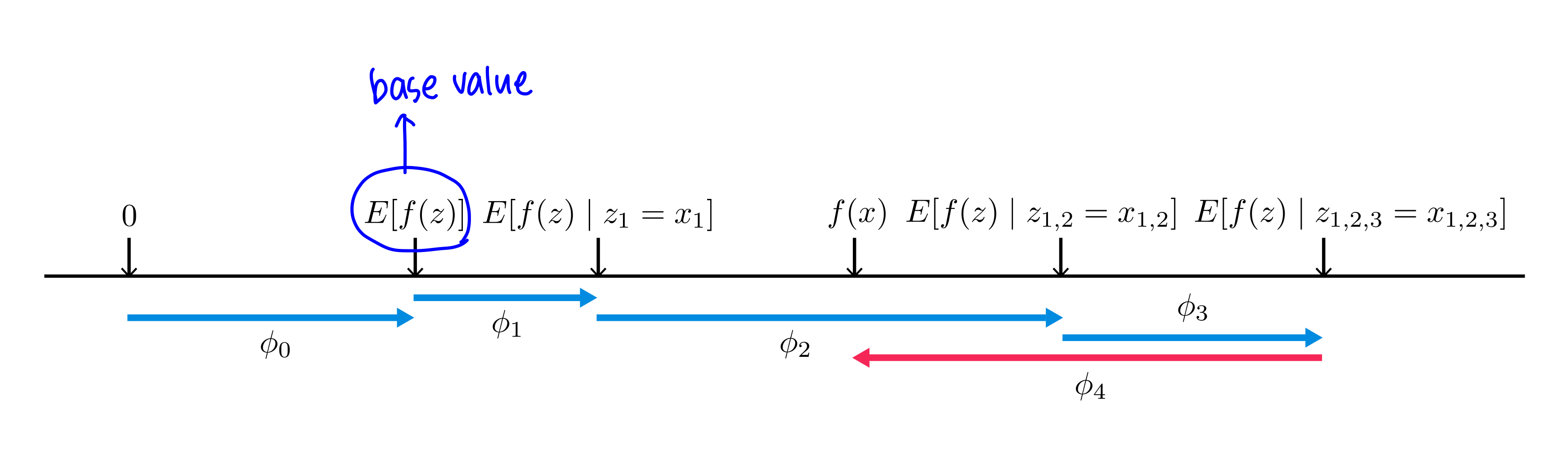
SHAP value는 이런 식으로 표현된다. 파란색 화살표는 예측을 약하게 만드는 feature들의 score, 분홍색 화살표는 예측을 강하게 만드는 feature들의 score이다.
이 부분은 SHAP을 파이썬으로 실습할 때 더 자세히 공부해보는걸로!

4-1. Model-Agnostic Approximations

: 어떤 모델이든 적용 가능함.

1) Kernel SHAP (Linear LIME + Shapley values)

* Theorem 2 (Shapley kernel)

$\Omega(g)=0$,
$\pi_{x'}(z')=\frac{(M-1)}{(M choose |z'|)|z'|(M-|z'|)}$,
$L(f,g,\pi_{x'}) = \sum_{z' \in Z} [f(h_x(z'))-g(z')]^{2} \pi_{x'}(z')$

• $L$: squared loss, $g(z')$: linear form

• 이 Theorem은 게임이론으로부터 온 Shapley value를 weighted linear regression과 잘 연결시킨다.

4-2. Model-Specific Approximations

1) Linear SHAP

• SHAP value는 모델의 coefficients로 정해진다.

* Corollary 1

$f(x) = \sum_{j=1}^{M} w_{j}x_{j}+b$, $\phi_{0}(f,x)=b$
$\implies \phi_{i} = w_{j} (x_{j}-E[x_{j}]])$

2) Low-Order SHAP

• $M$이 작을 때

3) Max SHAP

• 최댓값을 증가시킬 확률을 계산할 수 있다.

4) DeepSHAP(DeepLIFT + Shapley values)

• 피쳐들이 독립이고, deep model이 linear일 때.
• linear composition rule 사용: neural network의 비선형적인 부분을 선형화시키는 것.
• DeepSHAP은 각 성분에 대해 계산된 SHAP value에서 효과적인 선형화를 도출한다.

5. Computational and User Study Experiments

5.1 Computational Efficiency

• dense decision tree Model과 sparse decision tree Model에서 Shapley Sampling, SHAP, LIME을 비교하면, kernel SHAP의 향상된 샘플 효율성과 LIME의 값이 SHAP 값과 크게 다르다는 것을 알 수 있다.
• 즉, SHAP의 성능이 다른 평가지표보다 좋다는 것.

5.2 Consistency with Human Intuition

• 좋은 Model Explanation은 모델을 알고 있는 사람들이 하는 설명과 일관성이 있어야 한다.
• 두가지 실험을 진행함.

$\implies$ 2가지의 case를 통해, 사람의 설명과 SHAP이 아주 비슷한 경향을 보여주었다.

6. Conclusion

정확도와 모델 예측치의 해석 가능성에 대한 관심은 여러가지 방법론들을 만들어냈다. SHAP은 'additive feature importance methods'를 여러가지 기준으로 구별하였고, 앞서 언급한 3가지의 특성을 모두 만족하는 단 하나의 답이 있음을 보여주었다.

내 의견

프로젝트나 공모전 할 때, 예측 잘한다는 거 하나 믿고 머신러닝, 딥러닝 모델을 그냥 막 갖다 썼는데 이제는 쉽게 그러지 못할 것 같다. 갖다 쓰더라도 정확도에 대한 의심을 좀 할듯 ^^.
정확도가 높지만 왜 정확도가 높은지 실무자들에게 설득하기 위해서는 내가 이 결과를 해석할 줄 알아야 한다는 것을 깨달은 시간이었다. 당연한 건데 왜 이제서야 알았을까.
혹시나 프로젝트를 진행하거나 일하면서 머신러닝 같은 blackbox 모델을 쓰게 되면 이런 방법론을 사용해보자.

하지만 논문 말미에 실험한 것도 SHAP value가 인간의 판단과 비슷한지를 확인하는데, 인간이 판단할 수 없는 상황에서도 SHAP value를 믿을 수 있을지 의문이다.

일단 파이썬으로 실습해보면서 확인해보는걸로.