코플릿 데일리 코딩 02_fibonacci
어제 페어분과 재귀함수 연습문제를 풀면서 한번 보긴했는데 역시나 어렵다.(시간 복잡도, memoization...) 오늘은 일단 레퍼런스 코드와 친절한 블로그들의 풀이를 참고해서 이해해보도록 노력하고, 다음에 꼭 다시 내 힘으로 코드를 짜보는 걸로!
문제
아래와 같이 정의된 피보나치 수열 중 n번째 항의 수를 리턴해야 합니다.
0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1입니다. 그 다음 2번째 피보나치 수부터는 바로 직전의 두 피보나치 수의 합으로 정의합니다.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
- number타입을 인자로 받아 number타입을 출력해야 한다.
- 주의사항
재귀함수를 이용해 구현해야 합니다.
반복문(for, while) 사용은 금지됩니다.
함수 fibonacci가 반드시 재귀함수일 필요는 없습니다.
step1 재귀함수
일단 처음 0번째, 1번째를 제외하고는, n-1번째와 n-2번째 수의 합으로 n번째 피보나치의 수를 구할 수 있다. 재귀함수를 이용해서 풀면 아래와 같다.
function fibonacci(n) {
if(n <=1 )return n
return fibonacci(n-1) + fibonacci(n-2)
}재귀 함수로 5번째 피보나치 수를 구한다고 했을때, 함수 호출과정을 보면 동일한 연산이 중복해서 실행되는 것을 알 수 있다. (지금 입력 예시는 n이 5인 경우지만, 더 큰 수가 입력으로 들어올 경우에는 이 중복은 엄청난 비효율이다.)
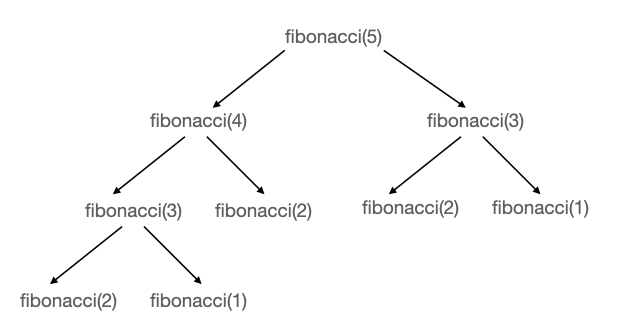
step2 재귀 + 메모지에이션
동일한 문제를 반복해야 하는 경우, 처음 수행한 연산을 기록해 두고, 다음에 수행할때 이 연산이 수행된 적이 있는지 확인한 다음, 이미 수행한 경우라면 기록되어 있는 값을 가져와서 사용한다. 이 메모지에이션(Memoization)을 이용해서 배열에 수행한 연산을 기록하고 이를 재활용한다.
function fibonacci(n) {
//(O(N))
//중복되는 계산을 메모해둔다.
const memo = [0, 1];
const aux = (n) => {
// 이미 해결한 적이 있으면, 메모해둔 정답을 리턴한다.
if (memo[n] !== undefined) return memo[n];
// 새롭게 풀어야하는 경우, 문제를 풀고 메모해둔다.
memo[n] = aux(n - 1) + aux(n - 2);
return memo[n];
};
return aux(n);
}
