백준에서 문제를 풀다가 정리하면 좋을 것 같은 알고리즘에 대해서 기록하고자 한다!

분할 정복

• 그대로 해결할 수 없는 문제를 작은 문제로 분할하여 문제를 해결하는 방법
• 큰 문제를 작은 문제로 쪼개고, 작은 문제를 해결한 다음 큰 문제를 해결하는 방식!
• 분할 정복 알고리즘의 설계 방식은 다음과 같다.

  1. 분할(Divde): 해결할 문제를 여러 개의 작은 부분 문제들로 분할
  2. 정복(Conquer): 나눈 작은 문제를 각각 해결
  3. 통합(Combine): 필요 시 해결된 해답을 모음

• 관련 문제 👉[BOJ] 2447번: 별 찍기 - 10
  위 문제의 문제 카테고리는 재귀/분할정복이다.

💻 BOJ 2447 코드

• 문제에서 핵심은 규칙을 찾아 이를 반복적으로 적용시켜주는 것이다.
  
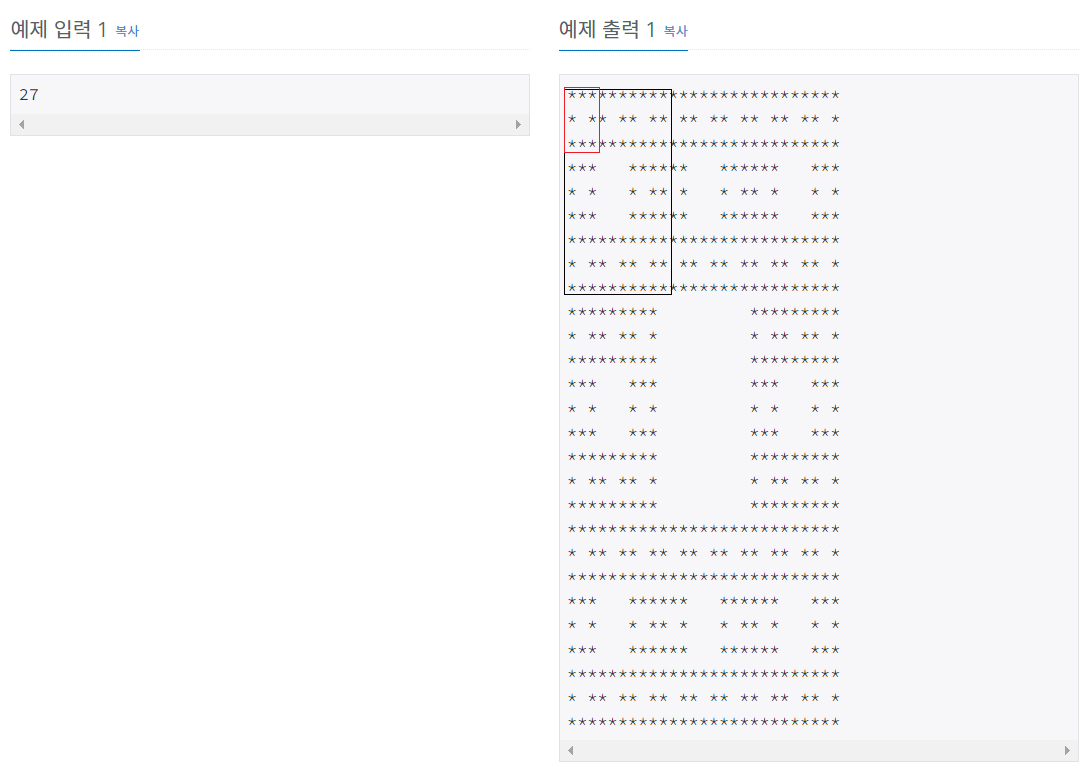
  예제 출력에서 볼 수 있다시피, N의 패턴은 중앙에 구멍이 나 있고, 주어진 기본 패턴이 반복되는 형태이다. N=27일 때 N=9인 정사각형이 들어있고, N=9일 때 N=3인 정사각형들이 안에 들어있다. 반복적으로 star를 make_star를 통해 호출하면서 해당하는 패턴을 출력해주면 되는 문제이다.
• cnt라는 변수를 설정해 주어 N을 3으로 나눠가며 cnt를 증가시킨다. 이 때 cnt는 make_star를 반복해주는 횟수이다.

def make_star(star):
    board = [] # 별을 그릴 보드
    for i in range(3*len(star)):
        if i // len(star) == 1:
            board.append(star[i%len(star)] + ' '*len(star) + star[i%len(star)])
        else:
            board.append(star[i%len(star)]*3)
    return board

star = ['***', '* *', '***']

N = int(input())
cnt = 0

while N > 3:
    N //= 3
    cnt += 1

for i in range(cnt):
    star = make_star(star)

for i in star:
    print(i)

병합 정렬

• 여러개의 정렬된 자료의 집합을 병합하여 하나의 정렬된 집합으로 만드는 방식
• 병합 정렬도 분할정복에 해당하는 알고리즘이다!
• 흔히 쓰이는 하향식 2-way 병합 정렬은 다음과 같이 작동한다.

  리스트의 길이가 1 이하이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는

  1. 분할(divide): 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
  2. 정복(conquer): 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
  3. 결합(combine): 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다. 이때 정렬 결과가 임시배열에 저장된다.
  4. 복사(copy): 임시 배열에 저장된 결과를 원래 배열에 복사한다.

• 관련 문제 👉[BOJ] 24060번: 알고리즘 수업 - 병합 정렬 1

백준 24060번 문제의 의사 코드를 바탕으로 파이썬 코드를 작성해보았다.

💻 코드 (Python)

# A를 오름차순 정렬한다
def merge_sort(A, p, r): # A[p, ... ,r]형태의 List
    if (p < r):
        q = (p+r)//2 # q는 p, r의 중간 지점
        merge_sort(A, p, q) # 전반부 정렬
        merge_sort(A, q+1, r) # 후반부 정렬
        merge(A, p, q, r) # 병합

# A[전반부]와 A[후반부]를 병합하여 오름차순 정렬된 상태로 만든다
def merge(A, p, q, r):
    i = p
    j = q+1
    tmp = []

    while (i<=q and j<=r):
        if (A[i] <= A[j]):
            tmp.append(A[i])
            i += 1
        else:
            tmp.append(A[j])
            j += 1
    
    while (i <= q): # 왼쪽 배열 부분이 남은 경우
        tmp.append(A[i])
        i += 1
    while (j <= r): # 오른쪽 배열 부분이 남은 경우
        tmp.append(A[j])
        j += 1

    i = p
    t = 0

    while (i <= r): # 결과를 A에 저장 
        A[i] = tmp[t]
        i += 1
        t += 1
    
    return A

병합정렬에 관한 다양한 코드가 있지만, 개인적으로 백준문제에서 나온 의사코드로 이해한 것이 제일 좋았다.

💻 BOJ 24060 코드

# A를 오름차순 정렬한다
def merge_sort(A, p, r): # A=[]
    if (p < r and cnt <=K):
        q = (p+r)//2 # q는 p, r의 중간 지점
        merge_sort(A, p, q) # 전반부 정렬
        merge_sort(A, q+1, r) # 후반부 정렬
        merge(A, p, q, r) # 병합

# A[전반부]와 A[후반부]를 병합하여 오름차순 정렬된 상태로 만든다
def merge(A, p, q, r):
    global cnt, result

    i = p
    j = q+1
    tmp = []

    while (i<=q and j<=r):
        if (A[i] <= A[j]):
            tmp.append(A[i])
            i += 1
        else:
            tmp.append(A[j])
            j += 1
    
    while (i <= q): # 왼쪽 배열 부분이 남은 경우
        tmp.append(A[i])
        i += 1
    while (j <= r): # 오른쪽 배열 부분이 남은 경우
        tmp.append(A[j])
        j += 1

    i = p
    t = 0

    while (i <= r): # 결과를 A에 저장 
        A[i] = tmp[t]
        cnt += 1
        if (cnt == K):
            result = A[i]
            break
        i += 1
        t += 1

N, K = map(int, input().split())
A = list(map(int, input().split()))
cnt = 0
result = -1 # 저장 횟수가 K보다 작으면 -1 출력
merge_sort(A, 0, N-1)
print(result)

작성한 병합정렬 코드에 변수 몇 가지만 추가해준 코드이다.
K번째 수를 구해줘야하니 K와, K를 구할 때 필요한 cnt, 그리고 K번째에 해당하는 수인 result를 선언해줬다.