📍문제

[프로그래머스] Lv.1 소수찾기

📍풀이

• 소수를 찾는 함수를 하나 더 만들어주고, solution에서 이를 for문으로 돌리며 찾아주기로 하였다.
  그러나...

💻나의 코드(오답)

def isPrime(n):
    for i in range(2, n):
        if n % i == 0:
            return False # 범위안에 나누어 떨어지는 수가 있으면 소수가 아님
    return True # 소수임

def solution(n):
    answer = 0
    # 마찬가지로 범위 안의 모든 수에 대하여 소수찾기 함수를 돌려줌
    for i in range(2, n+1):
        if isPrime(i) == True:
            answer += 1
    return answer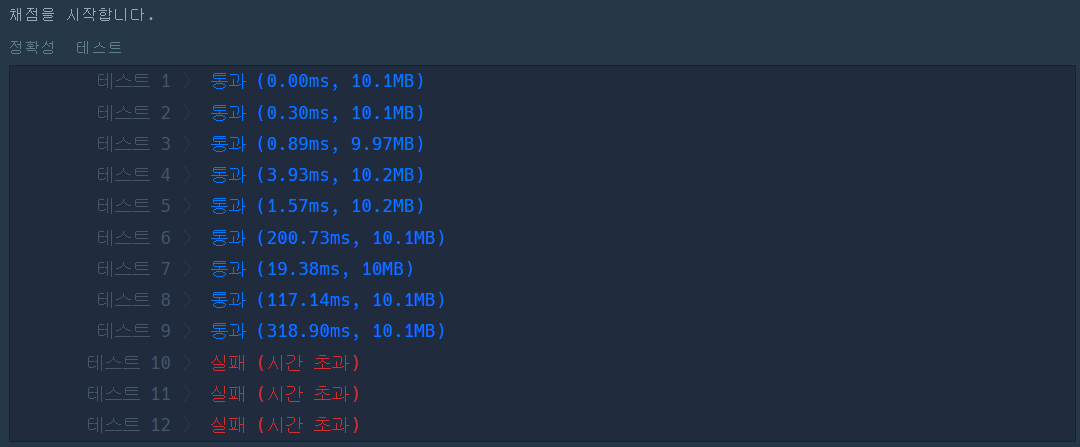

이렇게하면 시간초과가 뜸.
아무래도 제한조건 n은 2이상 1000000이하의 자연수입니다.에서 걸린 듯 하다.
위와 같이 알고리즘을 작성하는 경우 시간복잡도는 O(N)이다. 모든 경위의 수를 다 돌며 약수여부를 판별한다는 점에서 몹시 비효율 적이다. 사실은 O(N^(1/2))로 손 쉽게 계산할 수 있다. 예를 들면 8의 경우 2*4 = 4*2와 같은 식으로 대칭을 이루기 때문이다. 그래서 특정한 숫자의 제곱근까지만 약수의 여부를 검증하면 된다.

💻나의 코드(통과)

특정한 숫자의 제곱근까지만 약수의 여부를 검증하면 된다는점을 이용하여 코드를 다시 짰다.

import math
def isPrime(n):
    for i in range(2, int(math.sqrt(n))+1):
        if n % i == 0:
            return False
    return True

def solution(n):
    answer = 0
    for i in range(2, n+1):
        if isPrime(i) == True:
            answer += 1
    return answer

math모듈을 import해줘도 되고, import안할거면 n**(0.5)를 써주면 된다. 그렇게 해서 통과는 했으나..

효율성 10쓰레기임.
그렇다면 어떻게 더 효율적으로 코드를 짤 수 있을까!! 하면서 찾아보다보니까 많은 분들이 이 문제를 에라토스테네스의 체 알고리즘을 이용하여 풀었다는 사실을 발견!!

📖에라토스테네스의 체

대량의 소수를 한꺼번에 판별하고자 할 때 사용하는 것이라고 한다. 이 문제에 아주!! 적합한 알고리즘이라고 할 수 있다. (범위안의 모든 수를 탐색하면서 소수인지 아닌지 판별해야함)
에라토스테네스의 체는 가장 먼저 소수를 판별할 범위만큼 배열을 할당해 그 인덱스에 해당하는 값을 넣어주는 것이다.

1. 배열을 생성하여 값을 초기화 한다.
2. 2부터 시작해서 특정 숫자의 배수에 해당하는 숫자들은 모두 지운다. (그 특정 숫자는 제외한다. 예를 들어 2의 배수에 해당하는 숫자를 지운다면 2를 제외한 모든 수를 지우는 것)
3. 이미 지워진 숫자의 경우 건너뛴다.
4. 2부터 시작하여 남아있는 숫자들을 출력한다.

그렇다면 이를 순서대로 코드를 작성해보자!!

def solution(n):
    answer=0
    # 1. 배열을 생성하여 값을 초기화 한다. 모든 수가 소수(True)인 것으로 초기화,
    array=[True for i in range(n+1)]
    
    # 약수의 성질에 따라 가운데 약수(제곱근)까지만 확인해도 됨
    for i in range(2,int(n**(1/2))+1):
        if array[i]==True: # i가 소수인 경우
        	# 2. 특정 숫자의 배수에 해당하는 숫자들을 지운다. (i를 제외한 모든 배수를 지우기)
            j = 2
            while i * j <= n:
            	# 배수들을 지워주는 과정
                array[i*j] = False
                j += 1
    # 4. 남아있는 숫자들(True값인 것들만) 개수를 세준다.
    for i in range(2,n+1):
        if array[i]:
            answer+=1

    return answer

이렇게 해주면 훨씬 낫다 ㅋㅋㅋㅋㅋㅋㅋㅋ

⏱시간복잡도

에라토스테네스의 체 알고리즘의 시간 복잡도는 O(NloglogN)이라고 한다. 사실상 선형 시간에 동작할 정도로 빠르다고!! 다만 메모리가 많이 필요하다는 단점이 있다. 알고리즘을 수행할 때 N의 크기만큼의 리스트를 할당해야 하기 때문..!! 해당 문제의 제한조건에서도 n은 2이상 1000000이하의 자연수입니다.라는 조건을 보면.. N이 1000000일 경우 1000000까지의 모든 수에 대한 정보를 담을 수 있는 크기의 리스트가 필요하다.
그래서 만약 에라토스테네스의 체를 이용해야 하는 문제의 경우 N이 1000000이내로 주어지는 경우가 많다고 한다! 이론상 400만번 정도의 연산으로 문제를 해결할 수 있으며, 메모리또한 충분히 처리할 수 있는 크기만큼만 차지하게된다고~~하네요!!
알고리즘은 뭘까..
생각하게 되는 하루입니다..
왜 풀면 풀수록 어렵죠