📍문제

[프로그래머스] Lv.1 최대공약수와 최소공배수

📍풀이

• 두 수를 입력받고 1부터 둘 중 작은 수 까지 증가시켜주면서 나눴을 때, 동시에 나눠지는 숫자가 있다면 공약수이므로 이를 배열에 담아준다. 그 배열중 가장 큰 값이 최대공약수이다.
• 두 수를 입력받고 둘 중 큰 수 부터, 두 수의 곱까지의 숫자를 for문으로 돌면서 그 수를 n과 m으로 나웠을때 나머지가 0이라면 그 수가 최소공배수가 된다. 최소인 공배수를 구했으니 바로 break로 for문을 탈출하면 된다.

  💻나의 코드

def solution(n, m):
    answer = []
    arr1 = []
    for i in range(1, min(n, m)+1):
        if n%i == 0 and m%i ==0: # 동시에 나눠지면 공약수
            arr1.append(i)
    for i in range(max(n, m), (n*m)+1):
        if i%n == 0 and i%m == 0:
            min_num = i
            break
    max_num = max(arr1)
    answer.append(max_num)
    answer.append(min_num)
    return answer

answer에 각각 append해주면 출력 완. 근데 이제보니 굉장히 바보같은 코드다.
그냥 answer = [max_num, min_num] 해주면 되는 일이구나..
사실 오늘 이 문제에 대한 풀이를 적기 시작한 이유는 유클리드 호제법에 대해 기록하기 위해서다.
스터디에서 배웠던 내용인데 새까맣게 까먹다니..

📖유클리드 호제법

• 두 개의 자연수에 대한 최대 공약수를 구하는 대표적인 알고리즘
• 유클리드 호제법 : 두 자연수 A, B에 대하여 (A>B) A를 B로 나눈 나머지를 R이라고 할 때 A, B의 최대공약수는 B와 R의 최대공약수와 같다

def gcd(a, b):
    if a % b == 0:
        return b
    else:
        return gcd(b, a%b) # b와 a를 b로 나눈 나머지를 반환

두 수중 큰 수를 작은 수로 나눴을 때 나머지가 0이 되면 이것이 최대 공약수인데, 만약에 나누어 떨어지지 않는다면 B와 A를 B로 나눈 나머지인 R을 반환하는 재귀함수이다.

유클리드 호제법을 이용해 최소공배수 구하기

• 두 수를 곱한 것을 그 두 수의 최대공약수로 나누면 최소공배수가 된다.

def lcm(a, b):
	return (a*b) // gcd(a, b)

유클리드 호제법을 이용해 코드 수정

def gcd(n, m):
    if n%m == 0:
        return m
    else:
        return gcd(m, n%m)
    
def solution(n, m):
    answer = [gcd(m, n), n*m // gcd(m,n)]
    return answer

이렇게 실행시키면 속도가 월등히 빨라진 것을 확인할 수 있다.

유클리드 호제법을 이용한 다른사람 풀이

def gcdlcm(a, b):
    c, d = max(a, b), min(a, b)
    t = 1
    while t > 0:
        t = c % d
        c, d = d, t
    answer = [c, int(a*b/c)]
    return answer

이런식으로도 표현할 수 있다.

📋math.gcd와 math.lcm으로 구하기

math모듈을 임포트하여 사용할 수 있는 방법이다.
근데 프로그래머스에서 실행하면

AttributeError: module 'math' has no attribute 'lcm'

다음과 같은 에러가 뜸.
그래서 프로그래머스의 파이썬 버전을 확인해보니

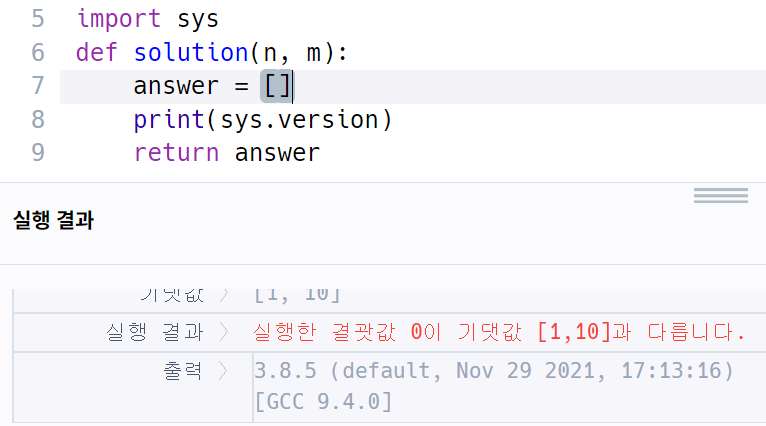
3.8.5더라..
lcm함수는 파이썬 3.9에서 추가된 함수라서 오류가 뜨는것~
이런게 있다고만 알아두고 관련 문제가 나오면 유클리드 호제법으로 푸는 방법을 이용하는것이 현명하겠당