🔎동적 계획법(Dynamic Programming)
이것이 취업을 위한 코딩 테스트다 with 파이썬을 참고하였습니다😃
- 한 번 계산한 문제는 다시 계산하지 않도록 하는 알고리즘
- 큰 문제를 작게 나누고, 같은 문제라면 한 번씩만 풀어 문제를 효율적으로 해결하는 알고리즘
피보나치 수열
재귀함수를 사용하는 대표적인 예시인 피보나치 수열 역시 동적 계획법으로 해결할 수 있다. 재귀함수로 나타내면 아래와 같다.
def fibo(n):
if n == 0:
return 0
elif n == 1 or n == 2:
return 1
else:
return fibo(n-1) + fibo(n-2)하지만 이렇게 재귀함수를 이용한 피보나치 수열 소스코드는 n이 커지면 커질수록 수행 시간이 기하급수적으로 늘어난다는 문제점이 있다. 일반적으로 O(2^n)의 시간복잡도를 가진다.
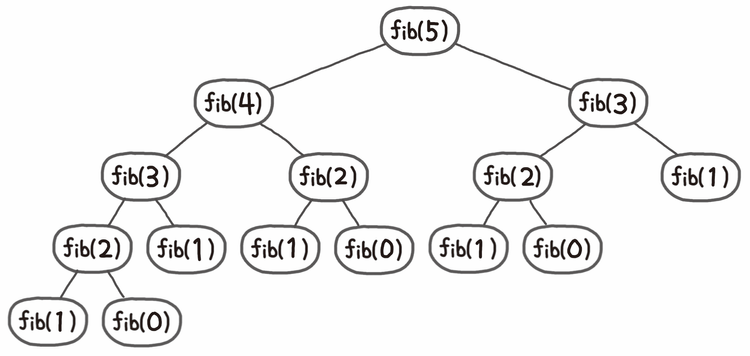
그림과 같이, 동일한 함수가 반복적으로 호출되지만, 이미 한번 계산한 값도 계속 호출할 때 마다 계산한다. 단순히 매번 계산하도록 하면 문제를 효율적으로 해결할 수 없다. 이럴 때 사용하면 좋은 동적 계획법!! 다음 조건을 만족할 때 사용할 수 있다.
- 큰 문제를 작은 문제로 나눌 수 있다.
- 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.
이를 따라서 피보나치 수열을 동적 계획법으로 나타내면 다음과 같다.
def fibo_dp(n):
dp = [0, 1, 1]
if n < 3:
return dp[n]
else:
for i in range(3, n+1):
# 계산된 결과를 저장하기
dp.append(dp[i-1]+dp[i-2])
return dp[n]이런 식으로 큰 문제를 해결하기 위해 작은 문제를 호출하는 방식을 탑다운(Top-Down)방식이라고 하며, 반면에 단순히 반복문을 이용하여 소스코드를 작성하는 경우 작은 문제부터 차근차근 답을 도출한다고 하여 보텀업(Bottom-Up)방식이라고 한다.
보텀업 방식으로 소스코드를 짜면 아래와 같이 나타낼 수 있다.
d = [0] * 100
d[1] = 1
d[2] = 1
n = 99
for i in range(3, n+1):
d[i] = d[i-1] + d[i-2]
print(d[n])📍문제
💻나의 풀이
dp리스트에 정수가 담긴 삼각형의 초기 정보triangle을 담아준다.
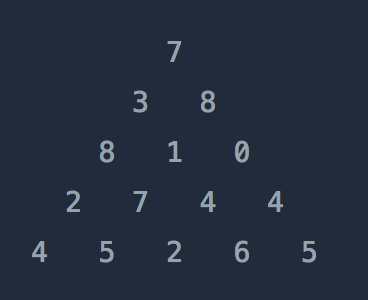
- 왼쪽 대각선 위에서 내려오는 경우, 두번째 줄의 3을 예로 들면, 왼쪽 대각선 위에는 수가 없으므로
upper_left_value에 0을 할당해줘야한다. (List index out of range를 예방하기 위한) - 왼쪽 대각선 위에서 내려오는 경우, 만약 두번째 줄의 8이라면 7을 가르키면 되므로
dp[i-1][j-1]를 할당해준다. - 오른쪽 대각선 위에서 내려오는 경우도 마찬가지로 처리해준다.
- 그렇게 해서 모든 자리에 누적합을
dp에 저장해준다. 위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다.이기 때문에,dp의 마지막 원소 중 가장 큰 수를answer에 할당해주면 된다!
def solution(triangle):
answer = 0
n = len(triangle)
dp = triangle
for i in range(1, n):
for j in range(len(triangle[i])):
# 왼쪽 대각선 위에서 내려오는 경우
if j == 0:
upper_left_value = 0
else:
upper_left_value = dp[i-1][j-1]
# 오른쪽 대각선 위에서 내려오는 경우
if j == i:
upper_right_value = 0
else:
upper_right_value = dp[i-1][j]
dp[i][j] = dp[i][j] + max(upper_left_value, upper_right_value)
answer = max(dp[-1])
return answer💻다른사람 풀이(강사님 코드)
# 정수 삼각형 강사님 풀이
def solution(triangle):
answer = 0
answer_list = [triangle[0]]
for i in range(1, len(triangle)):
# 해당 층의 길이 확인(합쳐지는 곳 체크)
len_row = len(triangle[i])
temp = []
# 인덱스와 값 확인
for j, v in enumerate(triangle[i]):
if j == 0:
temp.append(answer_list[i-1][0] + v)
elif j == len_row-1:
temp.append(answer_list[i-1[-1] + v])
else:
temp.append(v+max(answer_list[i-1][j-1], answer_list[i-1][j]))
answer_list.append(temp)
return max(answer_list[-1])로직 자체는 비슷한데 뭔가 더 이해하기 쉬운 코드이다.
여담인데 upper_right_value에서 오타가 나서 e를 하나 더 붙이는 바람에 자꾸 로컬변수가 선언되기 전에 사용됐다고 오류가 떴었다. 근데 그걸 못알아차리고 조건문의 문제인줄만 알고 ㅋㅋㅋㅋ(지금 생각해보면 if-else문인데 왜 선언이 안되는 조건이 있었을거라고 생각했는지 ㅡㅡ) 왜 안되는지만 끙끙거려 30분을 날렷음 ㄱ=
프로그래머스에서 직접 문제를 풀면 변수 오타가 나도 어디서 확인하기 쉽지 않다는게 문제인 듯 하다🥲
