기하 평균(Geometric Mean)

(a>0, b>0, c>0)

$\sqrt[2]{ab} ,\quad \sqrt[3]{abc}$

넓이가 ab 인 정사각형의 한변의 길이는 얼마인가?
부피가 abc 인 정육면체의 한변의 길이는 얼마인가?
$\vdots$

기하평균의 실제 사용사례

두 개의 주식이 있있는데,
두 주식 가격을 각 만원에 샀다고 하자.
1번 주식은 1일차 때 20%가 오르고, 2일차 때 20%가 내렸다.
2번 주식은 1일차 때 20%가 내리고, 2일차 때 20%가 올랐다.

내 주식의 가치는 떨어졌을까? 올랐을까?

• 1번 주식.

날짜	등락률	가격
1일차	20% ↑	10,000 + 2,000 = 12,000
2일차	20% ↓	12,000 - 2,400 = 9,600

• 2번 주식
  

날짜	등락률	가격
1일차	20% ↓	10,000 - 2,000 = 8,000
2일차	20% ↑	8,000 + 1,600 = 9,600

두 주식의 가격은 그대로 만원이 아니라 만원보다 작아집니다.

기존에 있던것에 20% 가 플러스 마이너스되는 것이 아니라, 순차적으로 하나의 계산이 이루어지고 나온 값이 다음 계산에 적용됩니다.

도형으로 생각

1번 주식에 대한 경우를 도형으로 생각해 봅시다.

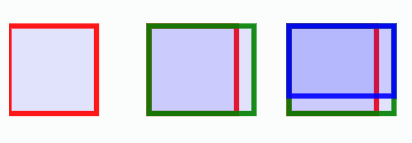
빨간색은 처음 주식의 가격입니다.
1일차 때는 한변의 길이가 현재의 1.2(20%) 로 늘어났습니다.
2일차 때는 한변의 길이가 현재의 0.8(20%) 로 줄어들었습니다.

최종적으로 마지막 사각형(파란색)과 처음 사각형(빨간색)을 비교하려고 하니, 어떤 사각형이 더 큰지 알수가 없습니다.

이럴 때, 기하평균으로써 생각해 봅시다.
모두 하나의 기준인 정사각형으로 통일해봅니다.

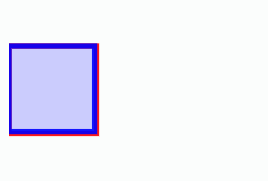
직사각형을 정사각형으로 변환하면, 두 도형이 완전히 겹치지 않고 '직사각형에서 정사각형으로 변환한 정사각형(파란색)'이 조금 더 작은것을 알 수가 있습니다.

이렇게 기하평균의 개념을 사용하면, 정사각형으로 변경하였을 때의 변의 길이를 비교하여 퍼센트 연산된 값을 비교해볼 수 있습니다.

이 예시에서는 2번의 퍼센트 연산이 일어났으므로 변이 두개인 정사각형을 생각했지만,
3번의 퍼센트 연산이 일어나면 정육면체, ... 계속해서 차원을 확장해서 고려해볼수 있습니다.